Introduction

The recent emergence of a novel severe acute respiratory syndrome corona-virus 2 (SARS-CoV-2) has caused a global pandemic with serious impacts on the public and environmental health and human welfare. The diameter of the virus varies between 60 and 140 nanometer (nm) with an average of 100 nm (1 nm = 10−9 m). The volume and mass of a single virus were estimated at 5.236 × 10−22 m3 and 7.07 × 10−19 kg, respectively (Aydin et al., 2020a; Zhu et al., 2020). Several studies (Anchordoqui & Chudnovsky, 2020; Aydin et al., 2020a; Gorbunov, 2020) determined its falling time and velocity regimes with(out) a respiratory droplet. When SARS-CoV-2 is transmitted through a respiratory droplet in the air, a better quantification of its falling dynamics entails the consideration of its evaporation regimes (Chong et al., 2021). In other words, the spread of SARS-CoV-2 in an indoor environment is closely coupled to its falling dynamics as a function of respiratory droplet diameter and evaporation. The Newtonian lift equation and Stokes’s law yield irrational results in terms of the motion dynamics beyond an apparent diameter range of micro-scale particles.

Aydin et al. (2020a) reported that the two models significantly differed in the falling time predictions of a SARS-CoV-2-laden respiratory droplet under the gravity with air resistance, in particular, when the droplet diameter was \(\le\) 100 and \(\ge\) 500 µm (µm). They also concluded that the Newtonian lift equation and Stokes’s law were applicable mostly to the droplet diameter \(\ge\) 237.5 µm and \(\le\) 237.5 µm, respectively. Similarly, Holterman (2003) and Giardina and Buffa (2018) pointed out that Stokes’s law was not applicable for droplet diameters > about 50 μm and overestimated the actual velocity considerably. Overall, Stokes’s equation appeared to be valid only for small Reynolds’s numbers. The two physical models still remain to be improved to better predict the falling time and velocity regimes of nanoscale particles laden with SARS-CoV-2. In the presence of air resistance, the light objects may exhibit Brownian motion and follow the pattern of turbulent convection in the air, depending on the particle size (Anchordoqui & Chudnovsky, 2020). The present study aimed to develop a simplified model in order to estimate the indoor falling dynamics of a SARS-CoV-2-laden respiratory droplet of 1 to 2000 μm in diameter from an infected person of 1.7 m in height. In other words, this study theoretically proposes a simple model to estimate the settling time of the virus-laden respiratory droplets of the different sizes and simulate their evaporation time, while they fall from an infected person with an average height of 1.7 m in the calm indoor air. In this way, not only was the evaporative demand of the indoor environment further accounted for, but also a minimum duration was determined for a new comer to enter an indoor space without protective measures immediately after an infected person leaves.

Materials and methods

The first deterministic epidemic analysis called susceptible-infected-recovered (SIR) was introduced in 1927 and consisted of ordinary differential equations as a non-linear system (Kermack & McKendrick, 1927). The algorithms for solving the spatiotemporal (3D space + time) spread of SARS-CoV-2 can be non-deterministic polynomial-time (NP)-hard in a dynamic outdoor environment (e.g., spatiotemporal changes in wind speed, direction, temperature, and population density). The deterministic models of both spread and falling dynamics generate outputs fully determined by their parameters and initial condition values (Das et al., 2020). Given the conditions of terminal/constant velocity, the following two approaches can be adopted (Aydin et al., 2020a). First, the combination of the Newton’s and modern lift equations yields the terminal velocity of the particle as follows:

$$\nu_{{{\text{NL}}}} = \sqrt {\frac{2mg}{{\kappa \rho_{{\text{a}}} A}}} ,$$
(1)

where \(\nu_{{{\text{NL}}}}\) is the downward terminal velocity (m s−1), \(m\) is the particle mass (kg), \(g\) is the gravitational acceleration (9.81 m s−2), \(\kappa\) is a shape-dependent coefficient such as 0.47 for water droplets of a spherical shape which was assumed as 1.99 for a single isolated SARS-CoV-2 due to its spikes, \(\rho_{{\text{a}}}\) is the air density (1.2041 kg m−3 at 20 °C and 1 atm); and \(A\) is the cross-surface area (m2). Equation (1) expresses the Newton’s laws of motion, Bernoulli’s equation, and Wright brothers’ ideas. Second, the combination of Newton’s and Stokes’s laws can be expressed thus:

$$v_{{{\text{NS}}}} = \frac{mg}{{6\pi \eta r}},$$
(2)

where \(v_{{{\text{NS}}}}\) is the final or terminal velocity (m s−1), \(\pi\) is 3.1416, \(r\) is the particle radius (m), and \(\eta\) is the dynamical viscosity of air (1.85 × 10−5 kg m−1 s−1) (Anchordoqui & Chudnovsky, 2020; Aydin et al., 2020a). Inspired by Aydin et al. (2020a), Hoeher et al. (2021) reproducibly took into account gravity and air drag. Similarly, our previous article (Aydin et al., 2020a) was included in a meta-analysis of 35 publications selected by an expert panel in order to decide risk factors to establish a semi-quantitative assessment of COVID-19 infections (Wang et al., 2021).

Assuming that the cross-surface area \((A)\) of a spherical object is equal to \(\pi r^{2}\) (where \(r\) is the radius of the sphere), Eqs. (1) and (2) can be rewritten as follows:

$$\nu_{{{\text{NL}}}} = \frac{{\sqrt {mg} }}{\pi r}\sqrt {\frac{2\pi }{{\kappa \rho_{{\text{a}}} }}} ,$$
(3)
$$v_{{{\text{NS}}}} = \frac{{\sqrt {mg} }}{\pi r}\frac{{\sqrt {mg} }}{6\eta }.$$
(4)

Taking the average of Eqs. (3) and (4) yields the following:

$$v_{{\text{t}}} = \frac{{\sqrt {mg} }}{2\pi r}\left( {\sqrt {\frac{2\pi }{{\kappa \rho_{{\text{a}}} }}} + \frac{{\sqrt {mg} }}{6\eta }} \right),$$
(5)

where \(v_{{\text{t}}}\) is the downward terminal velocity (m s−1) of the respiratory droplets. The cross-surface area of a single virus is assumed to equal the surface area of a hemisphere (\(2\pi r^{2}\)) where the base is not included, due to the wing area of its spikes (Aydin et al., 2020a). Thus, the expression of \(\sqrt {2\pi /\kappa \rho_{{\text{a}}} }\) in Eq. (5) can be parameterized as \(\sqrt {\pi /\kappa \rho_{{\text{a}}} }\) for a single SARS-CoV-2.

Although the velocity of a falling object is dependent upon the falling time, the predictions of the physical models show a wide variation for the falling time. The velocity of a micro- and/or nanoscale particle may not be constant due to its different particle size and distance, as well as possible convection of the air. Therefore, to obtain the best-fit curve to compare the estimations of the simplified Eq. (5) versus the other two models, the effective speed (\(v_{{{\text{SM}}}}\)) may be approximated by adopting the time constant with an increasing velocity as follows:

$$v_{{{\text{SM}}}} = (1 - 1/e) \times v_{{\text{t}}} ,$$
(6)

where e is a mathematical constant (the base of natural logarithm, a.k.a. Euler’s number ~ 2.718). The falling time \((t)\) of a single SARS-CoV-2 (whether be encapsulated by a droplet or not) from a given height \((h)\) in the calm indoor air can be quantified thus:

$$t = h/\nu_{{{\text{SM}}}} .$$
(7)

It is also well known that the droplets are subject to evaporation once they come out of the respiratory tract. The further the droplets are away from the mouth, the smaller the droplet size is due to evaporation. The precision and accuracy of the quantification of the environmental driving variables such as temperature and humidity influence the estimates of the motion dynamics, and thus, need to be improved (Anchordoqui & Chudnovsky, 2020). In this study, we have derived the following equation from the temperature, relative humidity, and pan evaporation data for the indoor conditions published by Yang et al. (2003):

$$E_{{\text{p}}} = 0.364\exp (0.084T_{{\text{a}}} ) + 3.64\exp ( - 0.021{\text{RH}}),$$
(8)

where \(E_{{\text{p}}}\) is pan-potential-evaporation (mm day−1), \(T_{{\text{a}}}\) is daily mean value of air temperature (in the range of 2–49 °C), and RH is relative humidity (in the range of 10–90%).

The evaporation rate is proportional to the surface area (Carrier et al., 2016) since water molecules are able to connect with air molecules on a large scale as a function of the rising surface area. The bending of an open water surface caused by surface tension creates an excess pressure, a.k.a. the Laplace pressure. However, the surface area of a spherical droplet (\(4\pi r^{2}\)) in the air exposed to the atmospheric evaporative demand is four times that of a droplet in an open water surface (\(\pi r^{2}\), the cross-surface area of a single droplet). Thus, the evaporation rate determined for an open water surface in an indoor environment can be multiplied by four to adjust the outcome for a respiratory droplet in the same air mainly for large droplets. In particular, the multiplication by four in order to account for the area of a spherical droplet is a reasonable simplistic assumption that led to the following equation for droplet evaporation (\(E_{{\text{d}}}\)):

$$E_{{\text{d}}} = 4 \times E_{{\text{p}}} .$$
(9)

Results and discussion

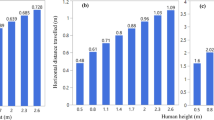
According to Eqs. (6) and (7), the falling velocity (\(v_{{{\text{SM}}}}\)) and time \((t)\) of a single SARS-CoV-2 from 1.7 m (a typical human height adopted in medical procedures) were estimated at 6.05 × 10−2 m s−1 and 281 s (roughly 5 min), respectively. Based on Eqs. (1), (2), and (6), and \(t = h/velocity\), the falling times of the respiratory droplets with the different diameters from 1.7 m are compared in Fig. 1. Overall, the predictions of our simplified model and the other two models were consistent for the falling times. The droplet diameter-dependent trajectory of the falling droplet laden with SARS-CoV-2 as a nanoscale object appeared to be better represented by the simplified model than the other two models, as was evidenced by its reasonable predictions for the wide range of the droplet diameter. Its falling time with a droplet diameter of about 300 μm remained almost the same among the three models (Fig. 1).

Fig. 1
figure 1

A comparison of falling times of a respiratory droplet with SARS-CoV-2 from 1.7 m as estimated from the Newtonian lift equation (NL), the Newton’s–Stokes’s laws (NS), and the simplified model (SM) suggested in this study

Full size image

The performance was evaluated comparing the evaporation rates estimated from Eq. (8) and data measured by Yang et al. (2003) (see Fig. 2). Given the measured temperature and RH data, Eq. (8) appeared to be applicable to the indoor environment, in particular, up to 90% RH. To further ascertain whether the falling time of a SARS-CoV-2-laden droplet from a given height is longer or shorter than its evaporation time, it is necessary to consider short-time variations in evaporation. Therefore, hourly percentages of daily evaporation derived by us from the data by Yang et al. (2003) are illustrated in Fig. 3. Overall, the evaporative demand increased as the day progressed and peaked at midday, and thus, the rate of evaporation at midday was ten times that at midnight. These important variations can be used to predict the evaporation time of the droplets at the different times of day.

Fig. 2
figure 2

A comparison of pan evaporation rates estimated (Ee) from Eq. (8) and according to data measured (Em) by Yang et al. (2003)

Full size image
Fig. 3
figure 3

Hourly percentages of daily evaporation data measured by Yang et al. (2003) for an indoor environment

Full size image

In order to compare the falling time of a droplet from a height and its evaporation time, the indoor room temperature was assumed as 22 °C. According to the US Environmental Protection Agency, the indoor relative humidity should be maintained ideally between 30 and 50%. Thus, 40% RH was assumed for the evaporation estimates.

The daily evaporation based on Eq. (8) was about 3.9 mm day−1 for an open water surface under the indoor conditions of 22 °C air temperature and 40% relative humidity. The evaporation rate determined for the open water surface was multiplied by four (see Eq. 9) in order to adjust the evaporation of a respiratory droplet in the same air. Chong et al. (2021) maintains that the square of a given diameter of an isolated evaporating spherical droplet may decline linearly over time. The detailed theoretical discussions of the evaporation of aqueous droplets were made by Holterman (2003) and Carrier et al. (2016). The theory by Abramzon and Sirignano (1989) should be considered in the evaporative estimations of the droplets in a fast-changing outdoor air condition.

The evaporation time scale of the droplets is shown in Table 1. Depending on their droplet diameter and time of day, the evaporation time of the droplets showed a great variation. Anchordoqui and Chudnovsky (2020) reported very short evaporation times for the wide range of droplet sizes of 50 to 2000 µm. The discrepancies between their and our studies can be attributed to the significant differences between the indoor and outdoor conditions for evaporation. For example, solar radiation, wind speed, temperature, and relative humidity are the most important drivers of the outdoor evaporation (Aydin et al., 2008; Aydin et al., 2020b). In this study, we only considered the effects of temperature and RH on evaporation under the indoor conditions. The exposed surface area of the droplets was also accounted for in the evaporation estimates. With a typical droplet diameter of 100 μm for sneezing, which may generate a size ranging from 1 to 1000 μm, the evaporation time was longer than the falling time. The diameter of the respiratory particles was reported to vary between 0.01 and 500 µm (rarely reaching 2000 µm), 95% of which fall into the range of 2–100 µm and to most commonly occur between 4 and 8 µm. Airborne and droplet particles were considered \(\le\) 5 and > 5 µm in diameter, respectively. According to World Health Organization and other agencies such as the Centers for Disease Control and Prevention (Bourouiba, 2020), the droplet diameters of 5 to 10 μm are categorized as host-to-host transmission droplets or aerosols. An equilibrium diameter of 10 μm is generally used in the risk analysis of airborne transmissions (Anchordoqui & Chudnovsky, 2020; Gralton et al., 2011). According to Table 1, the falling time of a respiratory droplet > 3 μm as a typical one of mouth spray from 1.7 m was shorter than its evaporation time based on a daily average. Such droplets reached the ground within the duration of evaporation (Fig. 4). However, the evaporation time of the respiratory droplet diameters as small as 3 μm was less than their falling time, thus leaving the droplet nuclei suspended in the air. In other words, large droplets settled faster than they evaporated, whereas small droplets evaporated faster than they settled (Bourouiba, 2020; Wells, 1934). Similarly, Bathula et al. (2021) reported that the diameter of the dry droplet nuclei decreased to 32% of the original diameter of the wet droplet due to evaporation. In the present study, the droplets with the diameters \(\le\) 1 and \(\le\) 6 μm were capable of complete evaporation and remained in the air for about 5 min as the droplet nuclei with SARS-CoV-2 at midnight and midday, respectively. Therefore, the droplets smaller than 1 μm were not taken into account since they evaporated faster than they settled down regardless of the day or night-time (Fig. 4). Inspired by our previous study (Aydin et al., 2020a), Hu et al. (2021) estimated the fog droplet size at the range of 4–6 μm based on its settling speed. However, the possible influence of a typical cloud of droplets was not factored in the estimation of droplet evaporation. Our simulations were independent of the host-dependent survival duration of SARS-CoV-2 suspended in the air. The lifetime of a droplet can change considerably from a fraction of a second to minutes. The half-life of SARS-CoV-2 in aerosols was estimated at about 1.1 h (Anchordoqui & Chudnovsky, 2020; Van Doremalen et al., 2020). Since we could not experimentally measure the processes due to technical difficulties, our suggested model needs further validation.

Table 1 Falling and evaporation times of a single SARS-CoV-2-laden respiratory droplet as a function of its diameter and times of day
Full size table
Fig. 4
figure 4

A comparison of falling and evaporation times of a respiratory droplet with SARS-CoV-2 in response to its diameters and times of day

Full size image

Conclusions

The Newtonian lift and Stokes’s equations yield an accurate description of the falling time only for a limited range of the droplet diameter. The simplified model adopted in this study better accounted for the motion dynamics of the wider range of the droplet size laden with SARS-CoV-2. The droplet diameter of about 300 μm from 1.7 m led to the same falling time regardless of the three models. The evaporation durations of the infected respiratory droplets under the indoor room temperature and RH were strongly related to their diameters and times of the day. Once the hourly rates of the indoor-air evaporative demand for the infected respiratory droplets were taken into account, the droplets \(\le\) 6 μm had shorter lifetimes at midday than their falling times. In other words, the droplets \(\le\) 6 μm were capable of complete evaporation during their fall and remained in the air for about 4.7 min as droplet nuclei with SARS-CoV-2. However, the motion of the light objects may follow the possible convection patterns in the air. Therefore, a minimum duration of 5 min would be required immediately after an infected person leaves an indoor space in order for a new comer to enter without protective measures. Our findings also bear some practical implications for preventing the spread of SARS-CoV-2. For example, the use of air conditioning systems that would only absorb indoor humidity would deprive SARS-CoV-2 of its carrying droplet and cause it to be suspended in the air for a longer time. Smoking would increase both the number of the SARS-CoV-2-laden droplets and their evaporation rate.