Modeling the effects of prosocial awareness on COVID-19 dynamics: Case studies on Colombia and India

Abstract

The ongoing COVID-19 pandemic has affected most of the countries on Earth. It has become a pandemic outbreak with more than 50 million confirmed infections and above 1 million deaths worldwide. In this study, we consider a mathematical model on COVID-19 transmission with the prosocial awareness effect. The proposed model can have four equilibrium states based on different parametric conditions. The local and global stability conditions for awareness-free, disease-free equilibrium are studied. Using Lyapunov function theory and LaSalle invariance principle, the disease-free equilibrium is shown globally asymptotically stable under some parametric constraints. The existence of unique awareness-free, endemic equilibrium and unique endemic equilibrium is presented. We calibrate our proposed model parameters to fit daily cases and deaths from Colombia and India. Sensitivity analysis indicates that the transmission rate and the learning factor related to awareness of susceptibles are very crucial for reduction in disease-related deaths. Finally, we assess the impact of prosocial awareness during the outbreak and compare this strategy with popular control measures. Results indicate that prosocial awareness has competitive potential to flatten the COVID-19 prevalence curve.

1 Introduction

The ongoing outbreak of coronavirus disease 2019 (COVID-19), caused by SARS-CoV-2 virus, a highly contagious virus, has been a massive threat for governments of many affected countries. COVID-19 is causing obstacles for public health organizations and is affecting almost every aspect of human life. The outbreak was declared a pandemic of international concern by WHO on March 11, 2020 [51]. The virus can cause a range of symptoms including dry cough, fever, fatigue, breathing difficulty and bilateral lung infiltration in severe cases, similar to those caused by SARS-CoV and MERS-CoV infections [15, 18]. Many people may experience non-breathing symptoms including nausea, vomiting and diarrhea [4]. Chan et al. [5] confirmed that the virus spreads through close contact of humans. It has become an epidemic outbreak with more than 50 million confirmed infections and above 1 million deaths worldwide as of October 31, 2020 [10].

Coronaviruses were first identified in 1965, since then these viruses have caused significant threat to human society. Although some of the coronaviruses caused minimal complications, few others have triggered major epidemic outbreaks in geographically diverse regions. Two of the outbreaks, namely severe acute respiratory syndrome (SARS) in mainland China in 2003 [16, 27] and Middle East respiratory syndrome (MERS) in South Korea in 2015 [9, 20], were observed in northeast Asia. In 2012, an outbreak of MERS in Saudi Arabia [11, 41] was observed which is in the middle east region. The SARS and MERS epidemic caused around 8000 and 2200 laboratory-confirmed cases, respectively [23]. Toward the end of 2019, a new coronavirus (COVID-19) that is genetically similar to SARS and MERS was identified in Wuhan, China. COVID-19 has lower case fatality rate than SARS and MERS, but it has significantly higher infection propagation rate. Profoundly affected countries implemented strict lockdown following the exponential rise in COVID-19 confirmed cases. However, due to high infectiousness the virus has spread to almost all the countries of the globe. Due to non-availability of vaccines and specific medications, non-pharmaceutical control measures such as social distancing, lockdown, use of mask, use of PPE kits and awareness through media are studied using different theoretical frameworks [24, 36, 42].

Mathematical models based on nonlinear differential equations may provide a suitable mechanism for the dynamics of COVID-19. Appropriate models can be used to test the efficacy of the control interventions against COVID-19. Several studies were performed using real data from profoundly affected countries and analyzed various features of the outbreak as well as assess the impact of interventions such as lockdown approaches to suppress the outbreak in the concerned countries [1, 22, 39, 42, 57]. There has been a few mathematical models to assess the impact of awareness campaigns against COVID-19 [6, 21, 34, 35, 55, 58]. These research articles mainly incorporate the awareness through media campaigns. The media effect is modeled in two ways: by adding media compartment to COVID-19 model [6, 21, 34, 58] and through reduction in incidence function due to media campaigns [35, 55]. However, there is a scope of investigating prosocial awareness on the dynamics of COVID-19 transmission. The idea is that the aware susceptible persons will pass the information (regarding use face mask, social distancing, mortality due to COVID-19, etc.) to the unaware susceptible individuals. The unaware people become aware by contacting the aware susceptible and practice the self-protection measures. In this process, the aware susceptibles have to take some risk in order to pass the information to unaware individuals. For this, we call it prosocial awareness.

As case studies, we use daily notified cases and deaths from Colombia and India. With over 50 million inhabitants, Colombia is the third-most-populous country in Latin America. On March 6, 2020, Colombia reported the first confirmed case of COVID-19. On March 17 , Colombian government declared a state of emergency due to COVID-19. The government imposed mandatory isolation for all adults over 70 years of age from March 20, 2020, to May 31, 2020. Elderly people were advised not to leave their residences unless there is an emergency. Moreover, local government administration was ordered to bring the necessary medicines and food to elderly people at their home. Afterward, a nationwide lockdown for 19 days was imposed from March 24, 2020 [52]. As of August 28, 2020, there were more than 590 thousand confirmed cases (currently, the world’s 7th highest) and above 18 thousand confirmed deaths [10]. As the outbreak of COVID-19 is expanding rapidly in Colombia, real-time analysis of epidemiological data is required to increase situational awareness and inform interventions. Mathematical modeling based on dynamic equations [13, 37, 46] may provide detailed mechanism for the disease dynamics. A few studies were based on the Colombia COVID-19 situation [2, 8, 38, 47]. The objectives and main findings of these studies are reported in Table 1.

Table 1 Related works on COVID-19 pandemic in Colombia

Table 2 Related works on COVID-19 pandemic in India

On the other hand, India is another country which is profoundly affected by COVID-19. On January 30, 2020, India reported its first case of COVID-19 in Thrissur, Kerala, which rose to three cases by February 3; all were students returning from Wuhan. Indian government implemented lockdown from March 25, 2020. Despite strict lockdown, India has reported more than 3 million cases as of August 28, 2020. Some studies are performed to reduce COVID-19 cases in India [7, 30, 42, 43]. Various control strategies have been proposed and analyzed. The objectives and main findings of these studies are reported in Table 2. These studies have broadly suggested that control measures could reduce the burden of COVID-19. However, none of the studies has considered awareness as a control utilizing recent epidemic data from Colombia and India.

The main objectives of this study are to (i) propose and analyze a compartmental model incorporating prosocial awareness, (ii) use available current COVID-19 epidemic (Colombia and India) and calibrate the proposed model and (iii) compare prosocial awareness with other popular control measures in Colombia and India.

Rest of the paper is organized as follows: A mathematical model which incorporates the prosocial awareness is described in Sect. 2. The equilibrium points of the model and their stability along with related conditions are presented in Sect. 3. In Sect. 4, the transcritical bifurcation phenomenon is presented between multiple equilibria. Next, in 5, we fit the proposed model to daily new COVID-19 cases and deaths from Colombia and India. The impact of prosocial awareness and comparison with other control strategies is also studied. Finally, in Sect. 6, we discuss the results from our study.

2 Model formulation

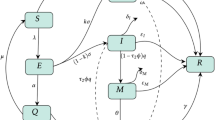
In this section, we describe the formulation of a mechanistic SEIR-type model for COVID-19 dynamics that incorporate prosocial awareness. A nonlinear system of differential equations is used to formulate the model. An SEIR (susceptible–exposed–infected–recovered) model for epidemic dynamics has been studied elsewhere [32, 33]. In the present context, the susceptible population is divided into two disjoint classes, namely unaware and aware susceptible population, where the aware people are those who apply at least one non-pharmaceutical intervention consistently (e.g., wear a mask, wear a face shield, maintain social distancing by staying 6 feet apart). Rest of the susceptible individuals are assumed to be unaware. The infected population is subdivided as notified COVID-19 people and un-notified people. Thus, we consider six mutually disjoint subclasses, viz. unaware susceptible class $(S_u(t))$, aware susceptible class $(S_a(t))$, exposed class (E(t)), un-notified infected class (I(t)), notified infected class (J(t)) and recovered class (R(t)). We denote by N(t) the sum of all classes, i.e., $N(t)= S_u(t) + S_a(t) + E(t) + I(t)+J(t)+ R(t)$ for all time $t>0$. Some known epidemiological factors are considered to model the pandemic along with newly incorporated prosocial awareness effect. However, a natural death rate ($\mu$) is considered for each class. A net influx of susceptible people is considered in the formulation at a rate of $\varPi$. Instead of constant awareness rate, we consider that the awareness will induce a behavioral response in the person and this person will transmit the knowledge to other hosts [12, 19]. Thus, unaware susceptibles can become aware through contact with aware susceptibles. The functional response in this regard is assumed to be $\frac{\alpha S_u S_a}{N}$. Both susceptible populations decrease due to infection through successful contact with infectives who may be notified or un-notified. Note that un-notified class contains both asymptomatic and symptomatic infected individuals. We assume that the transmission coefficient is smaller for notified individuals as they are kept under special observation. Thus, a reduced risk for notified COVID-19 patients is modeled as $\frac{\beta \nu J}{N}$ [32]. On the other hand for un-notified individuals, the standard mixing force of infection is formulated as $\frac{\beta I}{N}$ [33]. By making successful contact with infectives, both susceptible group members become exposed to the disease. The exposed population may become notified or un-notified at a rates $p \gamma$ and $(1-p) \gamma$, respectively. The recovery rate of un-notified and notified infected individuals are $\sigma _1$ and $\sigma _2$, respectively. The un-notified COVID-19 patients become notified at a rate $\eta$. The mortality rates related to COVID-19 are assumed to be $\delta _1$ and $\delta _2$ for un-notified and notified persons, respectively.

Fig. 1

Compartmental flow diagram of the proposed model

The flow diagram of the proposed model is displayed in Fig. 1.

From the above considerations, the following system of ordinary differential equations governs the dynamics of the system:

$$\begin{aligned} \displaystyle {\frac{\mathrm{d}S_u}{\mathrm{d}t}}= & {} \varPi - \beta \frac{I + \nu J}{N} S_u - \alpha \frac{S_a}{N} S_u - \mu S_u +\theta S_a, \\ \displaystyle {\frac{\mathrm{d}S_a}{\mathrm{d}t}}= & {} \alpha \frac{S_a}{N} S_u - \epsilon \beta \frac{I + \nu J}{N} S_a - (\mu + \theta ) S_a, \\ \displaystyle {\frac{\mathrm{d}E}{\mathrm{d}t}}= & {} \beta \frac{I + \nu J}{N} (S_u + \epsilon S_a)-(\gamma +\mu )E, \\ \displaystyle {\frac{\mathrm{d}I}{\mathrm{d}t}}= & {} (1-p) \gamma E - (\eta +\sigma _1+\mu + \delta _1)I, \\ \displaystyle {\frac{\mathrm{d}J}{\mathrm{d}t}}= & {} p \gamma E + \eta I - (\sigma _2+\mu + \delta _2)J, \\ \displaystyle {\frac{\mathrm{d}R}{\mathrm{d}t}}= & {} \sigma _1 I+\sigma _2 J-\mu R, \end{aligned}$$

All the parameters and their biological interpretation are given in Table 3, respectively.

Table 3 Description of parameters used in the model

3 Model analysis

3.1 Positivity and boundedness of the solution

This subsection is provided to prove the positivity and boundedness of solutions of the system (1) with following initial conditions

$$\begin{aligned} (S_u(0),S_a(0),E(0),I(0),J(0),R(0))^T\in {\mathbb {R}}_{+}^6. \end{aligned}$$

(1)

Proposition 1

The system (1) is invariant in ${\mathbb {R}}_{+}^6$.

Proof

Consider initial conditions (1), and let $S_u$ become zero at time $t_1$ before other state variables become zero, then

$$\begin{aligned} \frac{\mathrm{d}S_u}{\mathrm{d}t}|_{S_u=0}&=\varPi + \theta S_a \ge 0, \end{aligned}$$

at $t_1$. This shows that $S_u$ is a non-decreasing function of time at $t_1$. Hence, it follows that $S_u$ stays nonnegative. (Similar argument is employed in Theorem 3.1 of Sun et al. [45].) For other state variables, we note that

$$\begin{aligned} \frac{\mathrm{d}S_a}{\mathrm{d}t}|_{S_a=0}&= 0 \ge 0,\\ \frac{\mathrm{d}E}{\mathrm{d}t}|_{E=0}&=\beta \left[ \frac{(I+\nu J)}{S_u+S_a+I+J+R}\right] (S_u + \epsilon S_a)\ge 0,\\ \frac{\mathrm{d}I}{\mathrm{d}t}|_{I=0}&= (1-p) \gamma E\ge 0,\\ \frac{\mathrm{d}J}{\mathrm{d}t}|_{J=0}&=p \gamma E\ge 0,\\ \frac{\mathrm{d}R}{\mathrm{d}t}|_{R=0}&=\sigma _1 I + \sigma _2 J\ge 0. \end{aligned}$$

Thus, we obtain nonnegativity of all the six state variables and it follows that ${\mathbb {R}}_{+}^6$ is an invariant set for the model (1). $\square$

Proposition 2

The system (1) is bounded in the region

$\varOmega =\lbrace (S_u,S_a,E,I,J,R)\in {\mathbb {R}}_+^{6}|S_u+S_a+E+I+J+R\le \frac{\varPi }{\mu }\rbrace$

Proof

Adding all the equations of the model (1), total human populations satisfy the following equations,

$$\begin{aligned}&\frac{\mathrm{d}N}{\mathrm{d}t}=\varPi -\mu N-\delta _1 I - \delta _2 J \le \varPi -\mu N \end{aligned}$$

Since $\frac{\mathrm{d}N}{\mathrm{d}t}\le \varPi -\mu N$, it follows that $\frac{\mathrm{d}N}{\mathrm{d}t}\le 0$ if $N \ge \frac{\varPi }{\mu }$. Thus, by using standard comparison theorem, it can be shown that $N \le N(0) e^{-\mu t}+\frac{\varPi }{\mu }(1-e^{-\mu t})$. In particular, $N (t) \le \frac{\varPi }{\mu }$ if $N ( 0 ) \le \frac{\varPi }{\mu }$. Thus, the region $\varOmega$ is positively invariant. Further, if $N ( 0 ) > \frac{\varPi }{\mu }$, then either the solution enters $\varOmega$ in finite time, or N(t) approaches $\frac{\varPi }{\mu }$ asymptotically. Hence, the region $\varOmega$ attracts all solutions in ${\mathbb {R}}_+^{6}$. $\square$

3.2 Equilibrium points, threshold quantities and stability analysis

The system (1) has four types of equilibrium points: awareness-free disease-free equilibrium (AFDFE), disease-free equilibrium (DFE), awareness-free endemic equilibrium (AFEE) and endemic equilibrium (EE). The awareness-free, DFE is given by $E_0=(\frac{\varPi }{\mu },0,0,0,0,0)$.

Lemma 1

The awareness-free, DFE $E_0$ of system (1) is locally asymptotically stable whenever $\mathrm{max}\left[ R_1,\frac{\alpha }{\mu + \theta }\right] <1$ and unstable otherwise, where

$$\begin{aligned}&R_1=\frac{\beta \gamma }{(\mu + \gamma )(\sigma _2 + \mu + \delta _2)}\\&\qquad \quad \left[ (1-p)\frac{\eta \nu + \sigma _2 + \mu + \delta _2}{\eta + \sigma _1 + \mu + \delta _1} + \nu p \right] . \end{aligned}$$

Proof

We calculate the Jacobian of the system (1) at $E_0$, which is given by

$$\begin{aligned} J_{E_{0}}={\begin{pmatrix} -\mu &{} -\alpha + \theta &{} 0 &{} -\beta &{} -\beta &{} 0 \\ 0 &{} \alpha -(\mu +\theta ) &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} -(\mu +\gamma ) &{} \beta &{} \nu \beta &{} 0 \\ 0 &{} 0 &{} (1-p)\gamma &{} -(\eta +\sigma _1+\mu +\delta _1) &{} 0 &{} 0\\ 0 &{} 0 &{} p \gamma &{} \eta &{} -(\sigma _2+\mu +\delta _2) &{} 0 \\ 0 &{} 0 &{} 0 &{} \sigma _1 &{} \sigma _2 &{} -\mu \\ \end{pmatrix}}, \end{aligned}$$

Let $\lambda$ be the eigenvalue of the matrix $J_{E_{0}}$. Then, the characteristic equation is given by $det(J_{E_{0}}-\lambda I)=0$.

Clearly, $-\mu$, $-\mu$ and $\alpha - (\mu +\theta )$ are three eigenvalues of the Jacobian matrix $J_{E_0}$. The other three eigenvalues are given the following cubic equation

$$\begin{aligned} \begin{array}{lll} f(\lambda ):=\lambda ^3+a_1 \lambda ^{2}+a_2 \lambda +a_3=0\\ \end{array} \end{aligned}$$

(2)

where

$$\begin{aligned} a_1= & {} \mu + \gamma + m_1 +m_2\\ a_2= & {} (\mu + \gamma ) (m_1 +m_2) - \beta \gamma \\ a_3= & {} m_1 m_2 (\mu +\gamma ) (1-R_1). \end{aligned}$$

Here,

$m_1=\eta +\sigma _1+\mu +\delta _1$,

$m_2=\sigma _2+\mu +\delta _2$ and

$R_1=\frac{\beta \gamma }{m_2 (\mu + \gamma )} \left[ (1-p)\frac{\eta \nu + m_2}{m_1} + p \nu \right]$.

It is straightforward to show that coefficients of (2) satisfy Routh–Hurwitz criterion if $R_1<1$. Thus, all the eigenvalues are negative or have negative real parts if in addition $\frac{\alpha }{\mu + \theta }<1$.

On the other hand, if $\mathrm{max}\left[ R_1,\frac{\alpha }{\mu + \theta }\right] >1$, then at least one eigenvalue of the Jacobian matrix is positive and $E_0$ becomes unstable. Hence, the proof is complete. $\square$

Theorem 1

The awareness-free DFE $E_0$ is globally asymptotically stable for the system (1) if $\mathrm{max}\left[ R_1,\frac{\alpha }{\mu + \theta }\right] <1$.

Proof

The system (1) can be represented as

$$\begin{aligned} \frac{\mathrm{d}X}{\mathrm{d}t}&=F_1(X,V)\\ \frac{\mathrm{d}V}{\mathrm{d}t}&=G_1(X,V), G_1(X,0)=0 \end{aligned}$$

where $X=(S_u, S_a, R)\in R_3^+$ (uninfected classes of people), $V=(E, I, J)\in R_3^+$ (infected classes of people), and $E_{0}=(\frac{\varPi }{\mu },0,0,0,0,0)$ is the awareness-free, DFE of the system (1). The global stability of $E_0$ is guaranteed if the following two conditions are satisfied:

• 1. For $\frac{\mathrm{d}X}{\mathrm{d}t}=F_1(X,0)$, $X^*$ is globally asymptotically stable,

• 2. $G_1(X,V) = BV-{\widehat{G}}_1(X,V),$ ${\widehat{G}}_1(X,V)\ge 0$ for $(X,V)\in {\hat{\varOmega }}$,

where $B=D_VG_1(X^*,0)$ is a Metzler matrix and ${\hat{\varOmega }}$ is the positively invariant set with respect to the model (1). Following Castillo-Chavez et al. [3], we check for aforementioned conditions.

For system (1),

$$\begin{aligned} F_1(X,0)&=\begin{pmatrix} \varPi -\mu S_u\\ 0\\ 0 \end{pmatrix},\\ B&=\begin{pmatrix} -(\gamma +\mu ) &{} \beta &{} \nu \beta \\ (1-p) \gamma &{} -m_1 &{} 0\\ p \gamma &{} \eta &{} -m_2 \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} {\widehat{G}}_1(X,V)=\begin{pmatrix} \beta (I+\nu J) (1-\frac{S_u}{N})\\ 0\\ 0 \end{pmatrix}. \end{aligned}$$

Clearly, ${\widehat{G}}_1(X,V)\ge 0$ whenever the state variables are inside $\varOmega$. Also, it is clear that $X^*=(\frac{\varPi }{\mu },0,0)$ is a globally asymptotically stable equilibrium of the system $\frac{\mathrm{d}X}{\mathrm{d}t}=F_1(X,0)$. Hence, the theorem follows. $\square$

The unique disease-free equilibrium of the system (1) is given by

$$\begin{aligned} E_1=\left( \frac{\varPi (\mu +\theta )}{\mu \alpha },\frac{\varPi [\alpha -(\mu +\theta )]}{\mu \alpha },0,0,0,0\right) , \end{aligned}$$

which exists if $\frac{\alpha }{\mu +\theta }>1$. To obtain the basic reproduction number $R_0$ of the system (1), we apply the next-generation matrix approach. The infected compartments of the model (1) consist of (E(t), I(t), J(t)) classes. Following the next-generation matrix method, the matrix F of the transmission terms and the matrix V of the transition terms calculated at $E_1$ are,

$$\begin{aligned} F&=\begin{pmatrix} 0 &{} \quad \beta m_3 &{} \quad \nu \beta m_3 \\ 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 \\ \end{pmatrix},\\\\ V&=\begin{pmatrix} \gamma +\mu &{} \quad 0 &{} \quad 0 \\ -(1-p)\gamma &{} \quad m_1 &{} \quad 0 \\ - p \gamma &{} \quad -\eta &{} \quad m_2 \\ \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} m_1&= \eta + \sigma _1 + \mu + \delta _1\\ m_2&= \sigma _2 + \mu + \delta _2 \\ m_3&= \frac{1}{\alpha } \left[ (\theta + \mu ) + \epsilon \{\alpha - (\theta + \mu )\} \right] \end{aligned}$$

Calculating the dominant eigenvalue of the next-generation matrix $FV^{-1}$, we obtain the basic reproductive number as follows [49]

$$\begin{aligned} R_0=\frac{m_3 \beta \gamma }{m_2 (\mu + \gamma )} \left[ (1-p)\frac{\eta \nu + m_2}{m_1} + p \nu \right] . \end{aligned}$$

(3)

The basic reproduction number $R_0$ is defined as the average number of secondary cases generated by one infected individual during their infectious period in a fully susceptible population. The basic reproduction number $R_0$ of system (1) is given in (3).

Using Theorem 2 in [49], the following result is established.

Lemma 2

The disease-free equilibrium $\varepsilon _0$ of system (1) is locally asymptotically stable whenever $R_0<1$, and unstable whenever $R_0>1$.

Remark 1

Note that the threshold quantities $R_1$ and $R_0$ are linearly dependent by the relation $R_0=m_3 R_1$.

Theorem 2

The DFE $E_1$ of the model (1) is globally asymptotically stable in $\varOmega$ whenever $\mathrm{max}\left[ R_0,\right. \left. \frac{\beta \gamma }{(\sigma _1+\mu + \delta _1)(\mu + \gamma )},\frac{\beta \nu \gamma }{m_2(\mu + \gamma )}\right] <1.$

Proof

Consider the following Lyapunov function

$$\begin{aligned} {\mathcal {D}}=\frac{E}{\gamma + \mu }+\frac{I}{\gamma }+\frac{J}{\gamma } \end{aligned}$$

We take the Lyapunov derivative with respect to t,

$$\begin{aligned} \dot{{\mathcal {D}}}&=\frac{{\dot{E}}}{\gamma + \mu }+\frac{{\dot{I}}}{\gamma }+\frac{{\dot{J}}}{\gamma }\\&=\frac{1}{\mu +\gamma }\left[ \beta \frac{I + \nu J}{N} (S_u + \epsilon S_a)\right] \\&- \frac{(m_1 - \eta ) I}{\gamma } - \frac{m_2 J}{\gamma }\\&\le \frac{(\sigma _1+\mu + \delta _1) I}{\gamma } \left[ \frac{\beta \gamma }{(\sigma _1+\mu + \delta _1)(\mu + \gamma )} - 1\right] \\&\quad + \frac{m_2 J}{\gamma } \left[ \frac{\beta \nu \gamma }{m_2(\mu + \gamma )} - 1 \right] \\&\text { (Since }S_u + \epsilon S_a \le N\hbox { in } \varOmega ) \end{aligned}$$

Thus, $\dot{{\mathcal {D}}}\le 0$, whenever $\mathrm{max}\left[ \frac{\beta \gamma }{(\sigma _1+\mu + \delta _1)(\mu + \gamma )},\frac{\beta \nu \gamma }{m_2(\mu + \gamma )}\right] <1$.

Since all the variables and parameters of the model (1) are nonnegative, it follows that $\dot{{\mathcal {D}}}\le 0$ with $\dot{{\mathcal {D}}}=0$ at DFE if $\mathrm{max}\left[ \frac{\beta \gamma }{(\sigma _1+\mu + \delta _1)(\mu + \gamma )},\frac{\beta \nu \gamma }{m_2(\mu + \gamma )}\right] <1$. Hence, ${\mathcal {D}}$ is a Lyapunov function on $\varOmega$. Therefore, followed by LaSalle’s invariance principle [25], that

$$\begin{aligned} (E(t), I(t), J(t))\rightarrow (0,0,0) \text { as } t \rightarrow \infty \end{aligned}$$

(4)

Since $\lim \nolimits _{t\rightarrow \infty }\mathrm{sup} I(t)=0$ and $\lim \nolimits _{t\rightarrow \infty }\mathrm{sup} J(t)=0$ (from 4), it follows that, for sufficiently small $\xi _1>0, \xi _2>0$, there exist constants $L_1>0, L_2>0$ such that $\lim \nolimits _{t\rightarrow \infty }\mathrm{sup} I(t)\le \xi _1$ for all $t>L_1$ and $\lim \nolimits _{t\rightarrow \infty }\mathrm{sup} J(t)\le \xi _2$ for all $t>L_2$.

Hence, it follows that

$$\begin{aligned} \frac{\mathrm{d}R}{\mathrm{d}t}\le \sigma _1 \xi _1 + \sigma _2 \xi _2 - \mu R \end{aligned}$$

Therefore, using comparison theorem [44]

$$\begin{aligned} R^{\infty }=\lim \limits _{t\rightarrow \infty }\mathrm{sup} R(t)\le \frac{\sigma _1 \xi _1 + \sigma _2 \xi _2}{\mu } \end{aligned}$$

Therefore, as $(\xi _1,\xi _2) \rightarrow (0,0)$, $R^{\infty }=\lim \nolimits _{t\rightarrow \infty }\mathrm{sup} R(t)\le 0$

Similarly, by using $\lim \nolimits _{t\rightarrow \infty }\mathrm{inf} I(t)=0$ and $\lim \nolimits _{t\rightarrow \infty }\mathrm{inf} J(t)=0$, it can be shown that

$$\begin{aligned} R_{\infty }=\lim \limits _{t\rightarrow \infty }\mathrm{inf} R(t)\ge 0 \end{aligned}$$

Thus, it follows from above two relations

$$\begin{aligned} R_{\infty } \ge 0 \ge R^{\infty } \end{aligned}$$

Hence, $\lim \nolimits _{t\rightarrow \infty } R(t)= 0.$

Substituting $E(t) = I(t) = J(t) = R(t) = 0$ in the original system (1), we get

$$\begin{aligned} \displaystyle {\frac{\mathrm{d}S_u}{\mathrm{d}t}}&= \varPi - \frac{\alpha S_u S_a}{S_u+S_a} - \mu S_u +\theta S_a, \\ \displaystyle {\frac{\mathrm{d}S_a}{\mathrm{d}t}}&= \frac{\alpha S_u S_a}{S_u+S_a} - (\mu + \theta ) S_a, \end{aligned}$$

Following [50], a suitable Lyapunov function can be formulated as follows

$$\begin{aligned} {\mathcal {L}}&=\left[ (S_u - S_u^*) + (S_a-S_a^*) - (S_u^* + S_a^*) \text {ln} \frac{S_u+S_a}{S_u^* + S_a^*} \right] \\&\quad + \frac{2 \mu (S_u^* + S_a^*)}{\alpha S_a^*} \left( S_a - S_a^* - S_a^* \text {ln} \frac{S_a}{S_a^*}\right) , \end{aligned}$$

where $S_u^* = \frac{\varPi (\mu +\theta )}{\mu \alpha }$ and $S_a^* = \frac{\varPi [\alpha -(\mu +\theta )]}{\mu \alpha }$.

Therefore, by combining all above equations, it follows that each solution of the model equations (1), with initial conditions $\in \varOmega$, approaches $E_1$ as $t\rightarrow \infty$ for $\mathrm{max}\left[ \frac{\beta \gamma }{(\sigma _1+\mu + \delta _1)(\mu + \gamma )},\frac{\beta \nu \gamma }{m_2(\mu + \gamma )}\right] <1$. $\square$

3.2.1 Existence of awareness-free endemic equilibrium

Let $E_2=(S_u^*, 0, E^*, I^*, J^*, R^*)$ be any AFEE of system (1). Let us denote

$$\begin{aligned} m_1&=\eta +\sigma _1+\mu +\delta _1,\\ m_2&=\sigma _2+\mu +\delta _2,\\ m_4&=\frac{(1-p)\gamma }{m_1},\\ m_5&=\frac{p \gamma }{m_2} + \frac{\eta (1-p)\gamma }{m_1 m_2}. \end{aligned}$$

Further, the force of infection is

$$\begin{aligned} \lambda _h^*=\frac{\beta [I^* + \nu J^*]}{N^*} \end{aligned}$$

(5)

By setting the right equations of system (1) equal to zero, we have

$$\begin{aligned} S_u^*&=\frac{\varPi }{\lambda _h^* + \mu },\nonumber \\ E^*&=\frac{\lambda _h^*S_u^*}{\gamma + \mu }, I^*=m_4 E^*, \nonumber \\ J^*&=m_5 E^*, R^* =\frac{\sigma _1 m_4 E^* + \sigma _2 m_5 E^*}{\mu },\nonumber \\ N^*&=\frac{\varPi - \delta _1 m_4 E^* - \delta _2 m_5 E^*}{\mu }. \end{aligned}$$

(6)

Table 4 The local stability of equilibria for the model (1)

After simplification, we have the expression of $E^*$ as follows:

$$\begin{aligned} E^* = \frac{\varPi }{(\beta - \delta _1) m_4 + (\beta \nu - \delta _2)m_5}\left[ R_1 - 1 \right] , \end{aligned}$$

where $R_1$ is same as the threshold quantity for the AFDFE, given by

$$\begin{aligned} R_1=\frac{\beta \gamma }{m_2 (\mu + \gamma )} \left[ (1-p)\frac{\eta \nu + m_2}{m_1} + p \nu \right] . \end{aligned}$$

Therefore, the AFEE will exist if $R_1>1$ and $\beta > \mathrm{max}\{ \delta _1, \frac{\delta _2}{\nu }\}$.

3.2.2 Existence of endemic equilibrium

Let $E_{**}=(S_u^{**}, S_a^{**}, E^{**}, I^{**}, J^{**}, R^{**})$ be any endemic equilibrium of system (1). Let us denote

$$\begin{aligned} m_1&=\eta +\sigma _1+\mu +\delta _1, m_2=\sigma _2+\mu +\delta _2,\\ m_3&= \frac{1}{\alpha } \left[ (\theta + \mu ) + \epsilon \{\alpha - (\theta + \mu )\} \right] , m_4=\frac{(1-p)\gamma }{m_1},\\ m_5&=\frac{p \gamma }{m_2} + \frac{\eta (1-p)\gamma }{m_1 m_2}, m_6= \beta (m_4 + \nu m_5), m_7= \frac{\mu + \theta }{\alpha \mu }. \end{aligned}$$

Further, let the force of infection be

$$\begin{aligned} \lambda _h^{**}=\frac{\beta [I^{**} + \nu J^{**}]}{N^{**}} \end{aligned}$$

(7)

By setting the right equations of system (1) equal to zero, we have

$$\begin{aligned} S_u^{**}&=\frac{N^{**}}{\alpha } \left( \epsilon \lambda _h^{**} + \mu + \theta \right) , S_a^{**}\nonumber \\&=\frac{\varPi \alpha - N^{**}( \lambda _h^{**} + \mu )( \epsilon \lambda _h^{**} + \mu + \theta )}{\alpha ( \epsilon \lambda _h^{**} + \mu )},\nonumber \\ E^{**}&=\frac{\lambda _h^{**}(S_u^{**} + \epsilon S_a^{**})}{\gamma + \mu }, I^{**}=m_4 E^{**}, \nonumber \\ J^{**}&=m_5 E^{**}, R^{**} =\frac{\sigma _1 m_4 E^{**} + \sigma _2 m_5 E^{**}}{\mu },\nonumber \\ N^{**}&=\frac{\varPi - \delta _1 m_4 E^{**} - \delta _2 m_5 E^{**}}{\mu }. \end{aligned}$$

(8)

From Eqs. (7) and (8), we have

$$\begin{aligned} \lambda _h^{**}&=\frac{\beta (m_4 + \nu m_5) E^{**}}{N^{**}}\nonumber \\&=\frac{\beta (m_4 + \nu m_5) \lambda _h^{**}}{\mu + \gamma } \left( \frac{S_u^{**}}{N^{**}} + \epsilon \frac{S_a^{**}}{N^{**}}\right) \end{aligned}$$

(9)

This implies

$$\begin{aligned} \frac{\mu + \gamma }{\beta (m_4 + \nu m_5)}&=\frac{1}{\alpha } \left( \epsilon \lambda _h^{**} + \mu + \theta \right) \nonumber \\&\quad + \frac{\varPi \alpha \epsilon }{\alpha ( \epsilon \lambda _h^{**} + \mu ) N^{**}} \nonumber \\&\quad - \frac{\epsilon ( \lambda _h^{**} + \mu )( \epsilon \lambda _h^{**} + \mu + \theta )}{\alpha ( \epsilon \lambda _h^{**} + \mu )} \end{aligned}$$

(10)

Now, using expression of $N^{**}$ and Eq. (9), we have

$$\begin{aligned} \frac{\varPi }{N^{**}}=\mu + \frac{(\delta _1 m_4 + \delta _2 m_5)\lambda _h^{**}}{\beta (m_4 + \nu m_5)} \end{aligned}$$

(11)

Putting the value of $\frac{\varPi }{N^{**}}$ in Eq. (10) and simplifying, we obtain

$$\begin{aligned} \lambda _h^{**}=\frac{\alpha \mu (\mu + \gamma )(R_0 - 1)}{\epsilon (\mu + \gamma )\{\alpha - \mu (1 - \epsilon ) R_1\} - \alpha \epsilon (\delta _1 m_4 + \delta _2 m_5)} \end{aligned}$$

(12)

This indicates that the model 1 has unique endemic equilibrium if it exists. The existence criterion for the EE is $R_0>1$ and

$$\begin{aligned} \alpha (\mu + \gamma )>\mu (\mu + \gamma )(1 - \epsilon ) R_1 + \alpha (\delta _1 m_4 + \delta _2 m_5) \end{aligned}$$

.

The stability analysis of the equilibria for the model (1) is summarized in Table 4.

4 Numerical bifurcation analysis

In this section, various possibilities of forward transcritical bifurcations are examined based on the stability analysis of the four equilibrium points of the model (1). To do the numerical experiments, the initial conditions are assumed to be,

$$\begin{aligned} N&= 10000, S_u(0)=0.9 \times N,\\ S_a(0)&= 100, E(0)=100, \\ I(0)&= 10, J(0) = 10, R(0)=0. \end{aligned}$$

The fixed parameters used in this section are as follows: $\varPi =\mu \times N$, $\nu =0.05$, $\gamma =0.1$, $\eta =0.01$, $\sigma _1=0.05$, $\sigma _2=0.01$, $p=0.2$, $\delta _1=0.01$ and $\delta _2=0.003$.

From the stability analysis of the equilibria $E_0$ and $E_1$, it can be inferred that the $E_0$ will become unstable after a certain threshold of $\alpha$, namely $\mu +\theta$ whenever $R_1<1$. In this region, when $\alpha >\mu +\theta$, the DFE will become LAS whenever $R_0<1$. This phenomenon is depicted in Fig. 2a. This type of phenomenon is called forward transcritical bifurcation where the two equilibrium points switch their stability at a critical value.

Fig. 2

a Transcritical bifurcation for the aware susceptibles at equilibrium ($S_a^*$) of the model (1). Using the parameter values: $\mu =0.01$, $\beta =0.05$, $\theta =0.05$, $\epsilon =0.04$ and $0.001<\alpha <0.2$. For this parameter set, $R_1=0.4842$. b Transcritical bifurcation for the notified infected population at equilibrium ($J^*$) of the model (1). Using the parameter values: $\mu =0.03$, $\alpha =0.03$, $\theta =0.03$, $\epsilon =0.04$ and $0.1<\beta <0.25$. c Transcritical bifurcation for the notified infected population at equilibrium ($J^*$) of the model (1). Using the parameter values: $\mu =0.01$, $\alpha =0.3$, $\theta =0.01$, $\epsilon =0.1$ and $0.4<\beta <0.9$

Further, the forward transcritical bifurcation between the equilibria $E_0$ and $E_2$ is depicted in Fig. 2b. The reason behind this result is that the existence of $E_2$ depends on the threshold quantity $R_1$ of $E_0$. This result indicates that depending on parameter values, the awareness-free, DFE can become unstable and one of $E_1$ or $E_2$ will become stable.

Furthermore, the forward transcritical bifurcation between the equilibria $E_1$ and $E_3$ is depicted in Fig. 2c. The reason behind this result is that the existence of $E_3$ depends on the threshold quantity $R_0$ of $E_1$. This result indicates that depending on parameter values, the DFE can become unstable and $E_3$ will become stable.

5 Case study on Colombia and India COVID-19 data

5.1 Data description

As of August 28, 2020, there were more than 590 thousand cases and above 18 thousand deaths in Colombia. In India, there were more than 3 million cases and more than 60 thousand deaths on August 28, 2020. Daily COVID-19 notified cases and deaths in Colombia and India for the time period March 19, 2020, to August 24, 2020, are considered for our study. These 159 days COVID-19 notified cases and deaths for these two countries were collected from [10]. We use the first 149 data points to calibrate the unknown model parameters. In this time period, COVID-19 cases and deaths both display a upward trend for Colombia and India. This is an alarming situation as the pandemic continues to affect these countries. This is why we chose Colombia and India for case studies. However, we use the remaining 10 data points to check the accuracy of the fitted model. The demographic parameter values and initial conditions for fitting the proposed model to data are given in Tables 5 and 6.

Table 5 Demographic parameter values for Colombia and initial conditions

Table 6 Demographic parameter values for India and initial conditions

Table 7 Estimated parameter values of the model (1) for Colombia

Table 8 Estimated parameter values of the model (1) for India

5.2 Model calibration

We fit the model (1) to daily new notified cases and deaths of COVID-19 for both countries. Fixed parameters of the model (1) are given in Table 3. The demographic parameters and initial condition are reported in Tables 5 and 6. We estimate seven unknown model parameters, namely $\beta$, $\alpha$, $\nu$, $\epsilon$, $\eta$, $\delta _1$ and $\delta _2$, by fitting the model to newly daily reported cases and deaths. Additionally, two initial conditions of the model (1) were also estimated from the data, namely initial number of exposed individuals E(0) and initial number of un-notified individuals I(0). During the specified time period, nonlinear least square solver lsqnonlin (in MATLAB) is used to fit simulated daily data to the reported COVID-19 cases and deaths in Colombia and India. We used Delayed Rejection Adaptive Metropolis algorithm [17] to generate the 95% confidence region. An explanation of this technique for model fitting is given in [14]. The estimated parameters for Colombia and India are given in Tables 7 and 8, respectively. The fitting of the daily new notified COVID-19 cases and deaths of Colombia is displayed in Fig. 3, and the same is depicted in Fig. 4 for India.

Fig. 3

Model (1) fitting to daily notified COVID-19 cases and notified deaths due to COVID-19 in Colombia. Daily notified cases (deaths) are depicted in red dots, and purple curve is the model simulation. The blue dots are test data points in both panels. Gray shaded region is the 95% confidence region

Fig. 4

Model (1) fitting to daily notified COVID-19 cases and notified deaths due to COVID-19 in India. Daily notified cases (deaths) are depicted in red dots, and purple curve is the model simulation. The blue dots are test data points in both panels. Gray shaded region is the 95% confidence region

Using test data points (August 15, 2020, to August 24, 2020), we calculate two accuracy metrics for these 10 test data points: root-mean-squared error (RMSE) and mean absolute error (MAE). For the case fitting of Colombia, we found that RMSE = 2041.1 and MAE = 1520.9. On the other hand for fitting COVID-19 deaths in Colombia, RMSE = 186.7 and MAE = 150.09 are found. For India case fitting, fitted model yields RMSE = 5271.1 and MAE = 4335.2, and for death fitting, we found RMSE = 438.1 and MAE = 433.2. These results indicate that the fittings are quite good for both scenarios.

Fig. 5

Effect of uncertainty of the model (1) on the total number of deaths due to COVID-19 in a Colombia and b India. Parameters with significant PRCC indicated as *(p value < 0.05). The fixed parameters are taken from Table 3

Finally, we estimate the basic reproduction number $(R_0)$, for the proposed model (1). We draw 1000 samples of the estimated parameters from their posterior distribution obtained from the MCMC run and put them in the expression of $R_0$. All the fixed parameters are taken from Table 3 and Table 5. For Colombia, estimated values of $R_0$ are found to be 0.8415 with 95% confidence interval (0.4–1.19). The basic reproduction number for India is found to be 0.5271 with 95% confidence interval (0.3382–0.6583).

5.3 Sensitivity analysis

We performed global sensitivity analysis to identify most influential parameters with respect to the total deaths due to COVID-19 in 6-month time frame (starting from March 19, 2020). Let us denote by $D_{\mathrm{total}}$ the total number notified and un-notified deaths due to COVID-19. Partial rank correlation coefficients (PRCCs) are calculated and plotted in Fig. 5. Nonlinear and monotone relationship were observed for the parameters with respect to $D_{\mathrm{total}}$, which is a prerequisite for performing PRCC analysis. Following Marino et al. [31], we calculate PRCCs for the parameters $\beta$, $\alpha$, $\theta$, $\nu$ and $\epsilon$. The following response function is used to calculate the PRCC values

$$\begin{aligned} D_{\mathrm{total}}=\int _0^T [\delta _1 I(t) + \delta _2 J(t)]\text {d}t, \end{aligned}$$

where ${T}=180$ days (chosen arbitrarily). The base values for the parameters $\beta$, $\alpha$ and $\delta _2$ are taken as the mean of estimated parameters reported in Tables 7 and 8. The other base values are taken as the fixed values displayed in Table 3. For each of the parameters, 1000 Latin Hypercube Samples were generated from the interval (0.5 $\times$ base value, 1.5 $\times$ base value).

It is observed that the parameters $\beta$, $\nu$, $\delta _1$, $\theta$ and $\delta _2$ have significant positive correlations with $D_{\mathrm{total}}$. This indicates that transmission rate of COVID-19 will increase the total number deaths related to COVID-19. Besides, modification factor for notified patients and death rate of un-notified patients are positively correlated with $D_{\mathrm{total}}$. On the other hand, the learning factor related to aware susceptibles has significant negative correlation with the response variable. These results reinforce the fact that $\beta$, $\nu$ and $\alpha$ are very crucial for reduction of COVID-19 cases in both the countries.

Fig. 6

Effect of control parameters $\alpha$ and $\beta$, $\nu$ and $\epsilon$ on the notified COVID-19 cases in Colombia

5.4 Future projections and control scenarios

In this section, we focus on four controllable parameters, namely learning factor related to aware susceptibles ($\alpha$), transmission rate ($\beta$), modification factor for notified patients or equivalently the efficacy of notified case containment ($\nu$) and reduction in transmission coefficient for aware susceptibles ($\epsilon$). Transmission rate of COVID-19 can be reduced by social distancing, face mask use, PPE kit use and through use of alcohol-based hand wash [4, 26]. The parameters $\nu$ and $\epsilon$ can also be reduced through effective management of notified cases and through increased behavioral changes by aware susceptible, respectively. On the other hand, $\alpha$ should be increased to reduce the burden of COVID-19 in the society. It can be increased if the aware people show more prosocial activities. However, the results from global sensitivity analysis suggest that $\beta$ is most effective in terms of reduction in total COVID-19-related deaths. The parameters $\alpha$ and $\nu$ were also found significant with respect to the response function. Now, we visualize the impacts of these four parameters on the notified COVID-19 cases in Colombia and India. Using the estimated parameters (see Table 7), we predict notified infections in the coming 5 months (150 days) starting from August 15, 2020. The baseline curve is determined by simulating the model with fixed parameters from Table 3 and mean values of estimated parameters from Table 7. For different values of $\alpha$, $\beta$, $\nu$ and $\epsilon$, the case reduction in COVID-19 cases is depicted in Fig. 6. The values of these parameters are chosen as low, medium and high while comparing their impacts. We simulated the model with $\alpha = 0.15$, $\alpha = 0.3$ and $\alpha = 0.6$, see Fig. 6. Similarly, $\beta$ ($=0.25, 0.15, 0.05$), $\nu$ ($=0.45, 0.3, 0.15$) and $\epsilon$ ($=0.3, 0.2, 0.1$) were chosen.

Similarly, using the estimated parameters from Table 8, we predict notified infections in the coming 5 months (150 days) starting from August 15, 2020. The baseline curve is determined by simulating the model with fixed parameters from Table 3 and mean values of estimated parameters from Table 8. For different values of $\alpha$, $\beta$, $\nu$ and $\epsilon$, the case reduction in COVID-19 cases is depicted in Fig. 7.

Fig. 7

Effect of control parameters $\alpha$ and $\beta$, $\nu$ and $\epsilon$ on the notified COVID-19 cases in India

It can be observed that all the four controllable parameters show similar trends in case reduction. However, $\beta$ and $\nu$ show sharp decay in cases. Note that the scales of case reductions in Figs. 6 and 7 are similar, but we cannot quantify the effectiveness of the parameters directly. Therefore, we calculate percentage reductions in un-notified and notified COVID-19 cases in Colombia and India, see Tables 9 and 10. The fixed parameter values are taken from Table 3, while the values of other parameters are taken from Tables 7 and 8. We used the following basic formula to compute percentage reductions in the values of I(t) and J(t)

$$\begin{aligned} {\text {Percentage reduction}}=\frac{{\text {Base value}} - {\text {Model output}}}{\text {Base value}}\times 100. \end{aligned}$$

Table 9 Percentage reduction in un-notified and notified COVID-19 cases for different controllable parameter values in Colombia

Table 10 Percentage reduction in un-notified and notified COVID-19 cases for different controllable parameter values in India

From Table 9, it can be argued that $\beta$ is most effective in reduction of COVID-19 cases in Colombia. Maximum reduction in $\nu$ ($=0.15$) can reduce notified COVID-19 cases up to 72.59%. In case of India, $\nu$, $\alpha$ and $\beta$ show promising reduction in both notified and un-notified cases. Thus, learning factor related to aware susceptibles ($\alpha$) shows competitive potential to reduce the COVID-19 cases in both countries.

Finally, we calculate the time taken for the notified COVID-19 cases to reduce below 500, while the learning factor ($\alpha$) increases (see Fig. 8). The fixed parameters are taken from Table 3 and mean values of estimated parameters from Tables 7 and 8. It is observed that the time taken reduces significantly with increase in the parameter $\alpha$ in both countries. For instance, with baseline learning factor ($\alpha = 0.1105$), Columbia will need 700 days to reduce the notified COVID-19 cases below 500, but with learning factor 0.8, it will need less than 100 days only to reduce the notified cases below 500. Similarly for India, baseline value of $\alpha =0.0959$ will need more than 350 days to reduce the notified cases below 500. But if we increase $\alpha$ to 0.8, then less than 100 days will be taken to reduce the notified cases below 500. Therefore, the learning factor must be increased in order to decrease the duration of the COVID-19 pandemic.

Fig. 8

Time taken for the notified cases to reach less than 500 cases when $0< \alpha < 0.6$

6 Discussion and conclusion

This paper provides a deterministic model for the transmission dynamics of COVID-19 outbreak incorporating prosocial behavior. The model, which adopts standard incidence functions in a realistic way, allows COVID-19 to be transmitted by un-notified and notified individuals. To gain insight into its dynamic features, the model was rigorously analyzed. The findings obtained are as follows. There are four types of equilibrium points of the proposed model: awareness-free, disease-free equilibrium ($E_0$), disease-free equilibrium ($E_1$), awareness-free endemic equilibrium ($E_2$) and endemic equilibrium point ($E_3$). The awareness-free, disease-free equilibrium is found to be globally asymptotically stable under a parametric condition (($\mathrm{max}\{R_1, \frac{\alpha }{\theta + \mu }\}<1$)). The basic reproduction number ($R_0$) for the proposed model is calculated using the next-generation matrix method. The model has a locally stable disease-free equilibrium whenever the basic reproduction number is less than unity. The global stability condition for the DFE is also presented using Lyapunov function. From epidemiological point of view, global stability of the DFE ensures the eradication if the parameter values satisfy the required conditions. The existence and stability criteria of these four equilibria are presented in Table 4. Further, the two threshold quantities $R_1$ and $R_0$ are linearly dependent on each other by the relation $R_0=m_3 R_1$. Using a hypothetical parameter set, we show the stability switch or transcritical bifurcation between $E_0$ and $E_1$ (see Fig. 2a). Also, transcritical bifurcations are observed between the equilibria $E_0$ and $E_2$ (see Fig. 2b) and between $E_1$ and $E_3$ (see Fig. 2c). Biologically, these bifurcations indicate that the equilibrium states may switch from zero to a nonzero population size. For instance, transcritical bifurcations between the equilibria $E_0$ and $E_2$ and between $E_1$ and $E_3$ stipulate that the infected population may jump from zero state to nonzero state. Therefore, it would be better to maintain the threshold parameters in the regime where $E_0$ and $E_1$ are locally stable. (Local stability conditions are stated in Table 4.)

We calibrated the proposed model parameters to fit daily cases and death data of two countries during the time period of March 19, 2020, to August 14, 2020. Using estimated parameters, the basic reproduction number is found to be 0.8415 with 95% confidence interval (0.4–1.19) for Colombia. For India, the basic reproduction number is found to be 0.5271 (0.3582–0.6583). These numbers indicate the success of both the governments in containing of this deadly disease. This is also reflected on the current decreasing phase of the notified cases of COVID-19 in Colombia and India. Global sensitivity analysis is performed with respect to the total number of COVID-19-related deaths. Results indicate that transmission rate ($\beta$), modification factor ($\nu$) and learning factor related to awareness of susceptibles ($\alpha$) are very crucial for reduction in disease-related deaths. We have also investigated the impact of four controllable parameters on the prevalence of notified COVID-19 cases. From Figs. 6 and 7, it can be observed that different levels of controls can significantly reduce the burden of COVID-19 from the community. However, to better quantify the impacts, we calculate the percentage reduction using a simple formula. This reveals that reduction in transmission rate is most effective in reducing un-notified and notified COVID-19 cases (see Table 9 and 10). Increase in the learning factor ($\alpha$) has competitive potential to flatten the curve of COVID-19 in Colombia and India (see Fig. 8). This finding reinforces the need for amplified campaigns and awareness made by individual aware susceptible persons. Prosocial behavior is needed to combat this highly infectious pandemic disease. Along with verified control strategies, the governments should promote prosocial awareness by aware people. This will definitely benefit the case reduction as well as management of future COVID-19 cases.