Within Host Dynamics of SARS-CoV-2 in Humans: Modeling Immune Responses and Antiviral Treatments

Abstract

In December 2019, a newly discovered SARS-CoV-2 virus was emerged from China and propagated worldwide as a pandemic, resulting in about 3–5% mortality. Mathematical models can provide useful scientific insights about transmission patterns and targets for drug development. In this study, we propose a within-host mathematical model of SARS-CoV-2 infection considering innate and adaptive immune responses. We analyze the equilibrium points of the proposed model and obtain an expression of the basic reproduction number. We then numerically show the existence of a transcritical bifurcation. The proposed model is calibrated to real viral load data of two COVID-19 patients. Using the estimated parameters, we perform global sensitivity analysis with respect to the peak of viral load. Finally, we study the efficacy of antiviral drugs and vaccination on the dynamics of SARS-CoV-2 infection. Results suggest that blocking the virus production from infected cells can be an effective target for antiviral drug development. Finally, it is found that vaccination is more effective intervention as compared to the antiviral treatments.

Introduction

Coronaviruses are a large group of viruses that have the potential to transmit between hosts. These are enveloped in positive-sense, non-segmented RNA viruses belonging to the Coronaviridae family (Nidovirales order) and widely distributed in humans and other mammals [1]. The virus is responsible for a range of symptoms including fever, cough, and shortness of breath [1]. Some patients have reported radiographic changes in their ground-glass lungs, healthy or lower than average white blood cell lymphocyte, and platelet counts; hypoxemia; and deranged liver and renal function. Since first discovery and identification of coronavirus in 1965, three significant outbreaks occurred, caused by emerging, highly pathogenic coronaviruses, namely the 2003 outbreak of ”Severe Acute Respiratory Syndrome” (SARS) in mainland China [2, 3], the 2012 outbreak of ”Middle East Respiratory Syndrome” (MERS) in Saudi Arabia [4, 5], and the 2015 outbreak of MERS in South Korea [6,7,8]. These outbreaks resulted in more than 8000 and 2400 cases of SARS and MERS infections, respectively [9]. A newer and genetically similar coronavirus, called SARS-CoV-2, is responsible for coronavirus disease 2019 (COVID-19). The case fatality rate of COVID-19 is lower than SARS and MERS diseases but COVID-19 spreads more rapidly and infects more people. Despite strict intervention measures implemented in the region where the COVID-19 was originated, the infection spread locally and elsewhere very rapidly. COVID-19 has been declared a pandemic by the World Health Organization in January 2020. Since its first isolation in Wuhan, China in December 2019, it has caused outbreak with more than 208 million confirmed infections and more than 4 million reported deaths worldwide as of 15 August 2021. The affected countries around the globe are fighting the virus by implementing social distancing and isolation strategies. Fortunately, there are various vaccines available in the community and different drugs are also being approved. Multiple approaches are adopted in the development of Coronavirus vaccines: (a) inactivated or weakened virus vaccines, which use a form of the virus that has been inactivated or weakened so it does not cause disease, but still generates an immune response (e.g., Covaxin); (b) protein-based vaccines, which use harmless fragments of proteins or protein shells that mimic the COVID-19 virus to safely generate an immune response (e.g., Novavax, Covavax); (c) Viral vector vaccines, which use a safe virus that cannot cause disease but serves as a platform to produce coronavirus proteins to generate an immune response (e.g., Sputnik V, Ad26.COV2.S, Covishield, AZD1222) and (d) RNA and DNA vaccines, a cutting-edge approach that uses genetically engineered RNA or DNA to generate a protein that itself safely prompts an immune response (e.g., mRNA-1273, BNT162b2). Recently, several drugs are also developed for moderate to severe COVID-19 patients and some of them are in different phase of trial period. The 3rd phase trial of [10] in India predicts that tocilizumab plus standard care in patients admitted to hospital with moderate to severe COVID-19 has faster recovery and reduce the burden of intensive care. In addition, there are other drugs such as Sotrovimab, Bamlanivimab and Etesevimab, Casirivimab and Imdevimab which have shown significant efficacy and are approved for emergency uses by US Food and Drug Administration. Thus, non-pharmaceutical control measures such as hand washing, covering mouth when coughing are to be practiced with pharmaceutical control measures to contain the spread of COVID-19 more rapidly. However, researchers have been putting more effort into finding a solution to this pandemic situation [11,12,13].

In addition to medical and biological research, theoretical studies based on mathematical models may also play an important role throughout this anti-pandemic fight in understanding the epidemic character traits of the outbreak, in having to decide on the measures to reduce the spread and in understanding within-host patterns of virus transmission. While there are many mathematical models developed at an epidemiological level for COVID-19 [14,15,16,17] and there are many statistical models dedicated to COVID-19 research [18,19,20,21,22]. However, there are few within-host level studies to understand SARS-CoV-2 replication cycle and its interactions with the innate and adaptive immune responses [23,24,25,26,27,28,29,30]. In these previous studies, authors studied target cell models and target cell models with eclipse phase. Therefore, an unified framework with both innate and adaptive immune responses is necessary for the understanding of SARS-CoV-2 spread inside the human body. The human immune system is comprised of innate and adaptive immune responses. While the adaptive immune system is both fast and effective at targeting invasions by previously encountered pathogens, its role in host defence in the first days of a new infection is secondary to that of the innate immune system. Within host models are employed for the following reasons: (a) these models enable us to understand SARS-CoV-2 viral dynamics and its step-by-step evolution inside a particular human, (b) The model investigates the dynamics of infection, treatment and vaccination, not merely endpoints, (c) The model helps the community ask “what if” questions to guide experiments and interventions on a particular human and (d) By generalizing the model for a range of patients, the model can identify most effective targets for antiviral drug development.

Motivated by the above discussion, we aim to develop a within-host mathematical model of SARS-CoV-2 infection considering human immune responses. This model can be used as a basis for understanding characterized patterns of disease severity in humans. Moreover, we intend to use real viral load data from COVID-19-positive patients to calibrate the proposed model so that the parameters are realistic for further inference. The main goal is to compare the efficacy of various antiviral therapies (drugs and vaccines) and identify the most beneficial target.

The rest of the paper is organized as follows: in "The mathematical model", we formulate the compartmental model of within human SARS-CoV-2 transmission; the equilibrium points of the proposed model are analyzed and the basic reproduction number is obtained in "Equilibria and Basic Reproduction Number"; viral load time series, transcritical bifurcation, fitting model to real data and global sensitivity analysis are presented in "Numerical Simulation"; in "Model with Antiviral Treatment", we study the efficacy of antiviral drugs and vaccination; finally, the obtained results are discussed in "Discussion and Conclusion".

The Mathematical Model

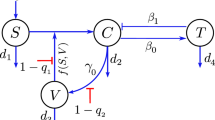
A deterministic ordinary differential equation model describing cell–virus–immune response interaction dynamics of SARS-CoV-2 infection is being formulated. Time-dependent state variables are taken to represent the compartments. A general mathematical model for the underlying dynamics of virus–host cell interaction has been studied in this context [23, 24]. However, the basic principles that underlay models of virus dynamics are as follows: Healthy uninfected cells, H(t), are infected when they meet free viruses, V(t). Infected cells, I(t), produce new virus particles that leave the cell and find other susceptible target cells. Whenever a human is infected with SARS-CoV-2, his innate and adaptive immune responses work together to neutralize the threat of SARS-CoV-2 infection [13, 31, 32]. The innate immune response works non-specifically and immediately after the viral attack. Cells and proteins of the innate immune system are ever-present in a healthy host and can respond to invading pathogens within the first minutes and hours of infection [33, 34]. This system is of great importance in the sense that it is preventing the establishment of new infections during the activation time of the adaptive immune system. It is believed that Cytokines are an essential component of the immune system [35]. They are a family of small soluble proteins secreted by different cells. They can be loosely classified into one of four families: the hematopoietins, the immunoglobin superfamily, the tumor necrosis factor family and the interferons (IFN). Cytokines modulate the balance between innate and adaptive immune responses. The IFNs are perhaps the most critical cytokines in the initial innate response to viral infection. They are classified into two types: IFN-$\alpha$ (a family of related proteins) and the single protein IFN-$\beta$ together form type I; IFN-$\gamma$ is the sole and unrelated type II IFN. IFN-$\alpha$ and IFN-$\beta$ are secreted by cells in response to viral infection and promote an antiviral response in otherwise susceptible cells. Cytokines C(t) is vital in inhibiting viral replication and modulating downstream effects of the immune response. Specific cytokines activate natural killer (NK) cells N(t), which play an essential role in killing virus-infected cells. As in [36, 37], the rate of NK cells increment caused by cytokines is assumed to be rC, whereas NK cells die at a rate $\mu _5$. Against the inhibiting mechanism of cytokines, the viruses often target the JaK/STAT pathway to decrease the production of IFNs. This mechanism, known as immunosuppression, has been observed for SARS-CoV-2 [38]. The functional form of a decrease in the cytokine production rate is assumed to be $\frac{k_2 I}{1 + \gamma V}$.

Meanwhile, cytokines also activate the adaptive immune system, mainly the cytotoxic T-lymphocytes T(t) at a rate $\lambda _1$. Interleukin-2 (IL-2) is a type of cytokine signaling molecule in the immune system that is very important to activate T-cells. T-cells finds virus infected cells and kill them at a rate $p_1$. T-cells subsequently activate B-lymphocytes B(t) at a rate $\lambda _2$ to produce antibody against the virus. B-cells mainly secrete IgM and IgG antibodies that are released in the blood and lymph fluid, where they specifically recognize and neutralize the SARS-CoV-2 viral particles [31, 35]. Meanwhile, antibody levels A(t) are increasing with the aim of halting infection (and in future providing protection against a subsequent infection). A schematic flow diagram of the model is depicted in Fig. 1.

Fig. 1

Schematic diagram of the proposed model. The blue arrows indicate production, black arrows indicate activation and orange ones show inhibition by different cells

Finally, the cell–virus–immune response interaction dynamics of SARS-CoV-2 infection are governed by the following system of differential equations:

$$\begin{aligned} \frac{dH}{dt}& = {} \varPi -\beta H V -\mu _1 H,\nonumber \\ \frac{dI}{dt}& = {} \beta H V- p_1 T I - p_5 N I - \mu _2 I,\nonumber \\ \frac{dV}{dt}& = {} k_1 I - p_2 CV - p_3 AV - \mu _3 V,\nonumber \\ \frac{dC}{dt}& = {} \frac{k_2 I}{1 + \gamma V} - \mu _4 C,\\ \frac{dN}{dt}& = {} rC - \mu _5 N,\nonumber \\ \frac{dT}{dt}& = {} \lambda _1 C T - \mu _6 T,\nonumber \\ \frac{dB}{dt}& = {} \lambda _2 T B - \mu _7 B,\nonumber \\ \frac{dA}{dt}& = {} G(t-\tau )\eta B - p_4 AV -\mu _8 A.\nonumber \end{aligned}$$

(1)

The time delay $\tau$ introduced through the Heaviside step function [39] is the time period that is required for the first production of antibodies after the T-lymphocytes and B-lymphocytes interact. This delay is biologically significant since the production of antibodies after the virions have associated with the B-lymphocytes is a complex process involving multiple steps. The B-cells have to undergo differentiations before they can be transformed into the plasma cells capable of producing antibodies [40]. The Heaviside step function G(t) is defined as follows,

$$\begin{aligned} G(t-\tau )&= 1, \text {if} \; \; t>\tau \\&= 0, \text {if} \; \; t<\tau . \end{aligned}$$

The model 1 has initial conditions given by: $H(0)=H_0 \ge 0$, $I(0)=I_0 \ge 0$, $V(0)=V_0 \ge 0$, $C(0)=C_0 \ge 0$, $N(0)=N_0 \ge 0$, $T(0)=T_0 \ge 0$, $B(0)=B_0 \ge 0$, and $A(0)=A_0 \ge 0$.

Table 1 Parameter values and their units of model 1

Note that innate immune system is non-specific defence mechanism of the body [43]. Therefore, the parameters are chosen irrespective of the virus. On the other hand, adaptive immune response is virus specific and the related parameters are chosen from SARS1498-CoV-2-related literature.

Equilibria and Basic Reproduction Number

In this section, dynamical analysis of the system is performed. Since the analysis is valid for $t -> \infty$, the delay term $\tau$ is assumed to be very small. There are four type of equilibria of the system (1), namely,

• (a) The disease free equilibrium (DFE) given by $E_0=(\frac{\varPi }{\mu _1},0,0,0,0,0,0,0)$.

• (b) The virus persistence equilibrium in the absence of immune responses, given by $E_1=(H_1,I_1,V_1,0,0,0,0,0)$, where $H_1=\frac{\varPi }{\mu _1 R_0}$, $I_1=\frac{\mu _1 \mu _3}{\beta k_1} (R_0 - 1)$ and $V_1=\frac{\mu _1}{\beta } (R_0 - 1)$ with $R_0=\displaystyle \frac{\varPi \beta k_1}{\mu _1 \mu _2 \mu _3}$. Clearly, this equilibrium exists only when $R_0>1$.

• (c) The virus persistence equilibrium in the absence of adaptive immune responses, given by $E_2=(H_2,I_2,V_2,C_2,N_2,0,0,0)$, where (assume, $Q=\beta H_2 V_2$) $H_2=\frac{\varPi - Q}{\mu _1}$, $N_2=\frac{r C}{\mu _5}$, $I_2=\frac{Q}{ \mu _2 + p_5 N_2}$, $V_2= \frac{1}{\gamma } \left[ \frac{k_2 I_2}{\mu _4 C_2}-1\right]$ and $C_2$ is given by the roots of the following cubic equation

  $$\begin{aligned} \frac{p_2 p_5 \mu _4 r}{\mu _5} C_2^3 + (\mu _2 \mu _4 p_2 + \frac{\mu _3 \mu _4 p_5 r}{\mu _5} )C_2^2&+\\ (\mu _2 \mu _3 \mu _4 + \mu _4 \gamma k_1 Q - k_2 p_2 Q)C_2 - k_2 \mu _3 Q&= 0. \end{aligned}$$

  Note that, irrespective of the sign of the coefficient of $C_2$, Descartes’ rule of sign ensure existence of exactly one positive root whenever $\frac{k_2 I_2}{\mu _4 C_2}>1$.

• (d) The all cells and virus co-existence equilibrium, given by

  $E_3=(H_3,I_3,V_3,C_3,N_3,T_3,B_3,A_3)$, where (assume, $Q=\beta H_3 V_3$) $H_3=\frac{\varPi - Q}{\mu _1}$, $I_3=\frac{\mu _4 \mu _6 R_1}{\lambda _1 k_2}$, $V_3= \frac{1}{\gamma }\left[ R_1 - 1\right]$, $C_3=\frac{\mu _6}{\lambda _1}$, $N_3=\frac{r C_3}{\mu _5}$, $T_3=\frac{\mu _7}{\lambda _2}$, $B_3=\frac{A_3}{\eta } [p_4 V_3 + \mu _8]$ and $A_3= \frac{1}{p_3 V_3} [R_2 - 1]$, with

  $$\begin{aligned} R_1=\frac{\lambda _1 k_2 Q}{\mu _4 \mu _6 (\frac{p_1 \mu _7}{\lambda _2} + \frac{r p_5 \mu _6}{\lambda _1 \mu _5}+ \mu _5)} \end{aligned}$$

  and

  $$\begin{aligned} R_2=\frac{\gamma \lambda _1^2 k_1 k_2 Q}{R_1 \mu _4 \mu _6(\lambda _1 \mu _3 + p_2 \mu _6)(R_1-1)}. \end{aligned}$$

  It can be noted that this equilibrium exists only when $R_1>1$ and $R_2>1$.

Theorem 1

The DFE $E_0$ of the system (1) is locally asymptotically stable, if $R_0<1$, and unstable if $R_0>1$, where

$$\begin{aligned} \displaystyle R_0=\displaystyle \frac{\varPi \beta k_1}{\mu _1 \mu _2 \mu _3}. \end{aligned}$$

(2)

Proof

The Jacobian of the system (1) at $E_0$ is given as

$$\begin{aligned} \begin{array}{llllllll} J(E_0)=\begin{bmatrix} -\mu _1 &{} 0 &{} -\frac{\beta \varPi }{\mu _1} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} -\mu _2 &{} \frac{\beta \varPi }{\mu _1} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} k_1 &{} -\mu _3 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} k_2 &{} 0 &{} -\mu _4 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} r &{} -\mu _5 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\mu _6 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\mu _7 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} G(t-\tau )\eta &{} -\mu _8\\ \end{bmatrix}.\\ \end{array} \end{aligned}$$

(3)

Clearly, $-\mu _1$, $-\mu _4$, $-\mu _5$, $-\mu _6$, $-\mu _7$ and $-\mu _8$ are eigenvalues of this Jacobean matrix and other two eigenvalues are given by the roots of the following equation

$$\begin{aligned} C(\varLambda ):= \varLambda ^2 + a_1 \varLambda +a_2= & {} 0, \end{aligned}$$

(4)

where

$$\begin{aligned} a_1&= \mu _2 + \mu _3\nonumber \\ a_2&= \mu _2 \mu _3 \left( 1-R_0\right) . \end{aligned}$$

(5)

Therefore, for $R_0<1$, the conditions for the Routh-Hurwitz criteria are satisfied and hence DFE is locally asymptotically stable. Now if $R_0>1$, then $a_2<0$ and $C(\lambda )=0$ will possess a positive real solution. Therefore the DFE will be unstable for $R_0>1$. Hence the proof follows. $\square$

The stability of the other three equilibrium points is complicated and does not lead to biologically relevant stability conditions. Therefore, we explore model solutions, relevant model dynamics, important parameters, agreement with real data through numerical simulations.

Numerical Simulation

In this section, important properties of the proposed model are investigated numerically. Using different parameter settings, time series and threshold analysis is performed. Moreover, the agreement of the model solution with real data is explored. Throughout this section, the following set of initial conditions is used unless stated $H(0)=4 \times 10^5$ cells per ml, $I(0)=3 \times 10^{-4}$ cells per ml, $V(0)=357$ RNA copies per ml, $C=0$ cells per ml, $N=100$ cells per ml, $T=500$ cells per ml, $B=100$ cells per ml and $A=0$ molecules per ml.

Time Series and Threshold Analysis

We first study the time series of the viral load and antibody count. In Fig. 2, the viral load and antibody are plotted. The viral load time series experiences a peak between sixth and seven days post infection. However, as soon as the adaptive immune response is activated (after $\tau =7$ days), a sharp decrease is observed in the viral load. On the other hand, the antibody count starts to rise after 7 days post infection and shows saturated type behavior.

Fig. 2

Time evolution of a viral load (V) and b antibody count (A) of the model 1. All the parameters are taken from Table 1 except $\beta = 2 \times 10^{-8}$, $\mu _2 =0.65$, $\mu _3=0.9$, $p_2=0.001$, $p_3=0.05$, $k_1=500$, $k_2=5$, $\eta =0.05$ and $\tau =7$

Further, we study the threshold for $R_0$. It is observed that $R_0=1$ acts as a critical value for the persistence of virus particles. The virus particles converge to the DFE of the model 1 for $R_0<1$ and the viral load converges to a non-zero value as soon as $R_0$ crosses unity. This type of phenomenon is called forward bifurcation where the two equilibrium points switches their stability at a critical value. The diagram is depicted in Fig. 3. This also ensure that if we vary other parameters involved in the expression of $R_0$, the same type of phenomenon occurs. Thus, in turn parameters such as $\beta$ and $k_1$ can be reduced so as to reduce $R_0$ below unity.

Fig. 3

Forward bifurcation diagram with respect to basic reproduction number. All the fixed parameters are taken from Table 1 with $\mu _2 =0.65$, $\mu _3=0.9$, $p_2=0.001$, $p_3=0.05$, $k_1=500$, $k_2=5$, $\eta =0.05$, $\tau =7$ and $10^{-9}< \beta < 10^{-7}$

Model Validation Using Real Data

SARS-CoV-2 viral load data are obtained from Wolfel et al. [44]. They studied patients from a hospital in Munich, Germany. They reported Daily measurements of viral load in sputum, pharyngeal swabs and stool for 9 patients. Among these patients, there were two patients (namely, patient A and patient B) for whom the growth phase of sputum data was captured. We therefore utilized these two datasets for our analysis. The data was collected from Wolfel et al. [44] using a online software [45]. The data for patient A and patient B are reported in Table 2 (Appendix A).

The solution curve of viral load (V(t)) is fitted to data using the built-in (MATLAB, R2018a) simplex algorithm to minimize the sum of squares difference between simulated indicators and data. We used the MATLAB function ‘fminsearchbnd’ to perform the optimization. During the computation, 100 different starting points in parameter space were chosen using Latin Hypercube Sampling to ensure consistency and uniqueness of the parameter estimates. The fitting is displayed in Fig. 4a for patient A and in Fig. 4b for patient B. The fixed parameters are taken from Table 1 with $\mu _2 =0.65$, $k_2=5$ and $\eta =0.05$. The initial conditions are taken as mentioned in the beginning of "Numerical Simulation". We estimated five parameters directly related to viral load of a patient viz., $\beta$, $k_1$, $p_2$, $p_3$ and $\mu _3$. The estimated parameters for patient A are found to be $\beta =1.7505 \times 10^{-6}$, $k_1=379$, $p_2=0.2805$, $p_3=0.0316$ and $\mu _3=0.8108$. Similarly, the estimates for patient B are obtained as $\beta =5.561 \times 10^{-7}$, $k_1=128$, $p_2=0.9403$, $p_3=0.0057$ and $\mu _3=0.99$.

Fig. 4

Fitting model solution to a patient A data and b patient B data

Sensitivity Analysis

We performed global sensitivity analysis to identify most influential parameters with respect to the maximum size (or alternatively, the peak of load) of virus particles ($V_{max}$) in 3 months time frame. Partial rank correlation coefficients (PRCCs) are calculated and plotted in Fig. 5. Nonlinear and monotone relationship were observed for the parameters with respect to $V_{max}$, which is a prerequisite for performing PRCC analysis. Following Marino et. al [46], we calculate PRCCs for the parameters $\beta$, $k_1$, $k_2$, $\mu _2$, $\mu _3$, $p_2$, $p_3$, $\gamma$ and $\eta$. The base values for the parameters $\beta$, $k_1$, $p_2$, $p_3$ and $\mu _3$ are taken as the average of estimated parameters of patient A and patient B. The other base values are $\mu _2 =0.65$, $k_2=5$, $\gamma =0.5$ and $\eta =0.05$. For each of the parameters, 500 Latin Hypercube Samples were generated from the interval (0.5 $\times$ base value, 1.5 $\times$ base value).

Fig. 5

Effect of uncertainty of the model (1) on the peak of viral load. Parameters with significant PRCC indicated as $^*$ (p-value < 0.05). The fixed parameters are taken from Table 1 with $\mu _2 =0.65$, $k_2=5$, $\eta =0.05$ and $\tau =7$

It is observed that the parameters $\beta$, $k_1$ and $\gamma$ has significant positive correlations with $V_{max}$. This indicates that the production rate of virus particles from infected cells will increase the chance of larger infection propagation. Besides, the infection rate and the immunosuppression rate are positively correlated with the peak of viral load. On the other hand, the natural death rate of infected cells and death rate of virus particles will have significant negative correlation with $V_{max}$. The production rate of cytokines is also negatively correlated with $V_{max}$. These results reinforces the fact that $\beta$ and $k_1$ are very crucial for reduction of viral load.

Model with Antiviral Treatment

Antiviral drugs can be used to slow SARS-CoV-2 infection or block production of virus particles. These drugs will necessarily save the lives of many severely ill patients and will reduce the time spent in intensive care units for patients, vacating hospital beds. Antiviral medications will, in turn, inhibit subsequent transmission that could happen if the drugs were not given. However, to analyze the effect of antiviral treatment, we consider drugs can block infection and/or production of virus particles. Many studies have suggested various existing compounds for testing [13, 47,48,49] as SARS-CoV-2 antiviral drug. Recently, several drugs are developed for moderate to severe COVID-19 patients and some of them are in different phase of trial period. The 3rd phase trial of [10] in India predicts that tocilizumab plus standard care in patients admitted to hospital with moderate to severe COVID-19 has faster recovery and reduce the burden of intensive care. In addition, there are other drugs such as Sotrovimab, Bamlanivimab and Etesevimab, Casirivimab and Imdevimab which have shown significant efficacy and are approved for emergency uses by US Food and Drug Administration.

Following Zitzmann et al. [50], we incorporate antiviral drug treatment in the proposed model (1). The effect of antiviral drugs can be either block infection ($\epsilon _1$) or block production of viral particles ($\epsilon _2$). The newly infected term $\beta HV$ now takes the form $(1-\epsilon _1) \beta HV$ and the production of viral particles $k_1 I$ becomes $(1 - \epsilon _2) k_1 I$. Thus, the modified system with antiviral treatment is given by

$$\begin{aligned} \frac{dH}{dt}& = {} \varPi - (1-\epsilon _1)\beta HV -\mu _1 H,\nonumber \\ \frac{dI}{dt}& = {} (1-\epsilon _1)\beta HV- p_1 TI - p_5 NI - \mu _2 I,\nonumber \\ \frac{dV}{dt}& = {} (1-\epsilon _2) k_1 I - p_2 CV - p_3 AV - \mu _3 V,\nonumber \\ \frac{dC}{dt}& = {} \frac{k_2 I}{1 + \gamma V} - \mu _4 C,\\ \frac{dN}{dt}& = {} rC - \mu _5 N, \nonumber \\ \frac{dT}{dt}& = {} \lambda _1 TC - \mu _6 T,\nonumber \\ \frac{dB}{dt}& = {} \lambda _2 BT - \mu _7 B,\nonumber \\ \frac{dA}{dt}& = {} G(t-\tau )\eta B - p_4 AV -\mu _8 A.\nonumber \end{aligned}$$

(6)

The reproduction number under antiviral treatments or the control reproduction number takes is found to be

$$\begin{aligned} \displaystyle R_c=\displaystyle \frac{(1-\epsilon _1)(1-\epsilon _2)\varPi \beta k_1}{\mu _1 \mu _2 \mu _3}. \end{aligned}$$

(7)

By following the steps of Theorem 1, it can be easily found that the basic reproduction number for the model with antiviral treatment is $R_c$. From expression of $R_c$, it can be noted that $R_c<R_0$ always hold.

Fig. 6

Effect of antiviral drugs that a reduce infection or b blocks virus production. The time series of viral load is presented for different values of $\epsilon _1$ and $\epsilon _2$. The fixed parameters are taken from Table 1 with $\mu _2 =0.65$, $k_2=5$, $\eta =0.05$ and $\tau =7$. Other fixed values are taken to be the average of estimated parameters for patient A and patient B

From Fig. 6, it can be noted that increase in $\epsilon _1$ reduces the peak of viral load but the duration of high viral load remains same. On the other hand, increase in $\epsilon _2$ significantly reduce both peak of viral load and duration of high viral load. Thus, we conclude that blocking the virus production from infected cells is a more suitable target for antiviral drug development.

Finally, we study the effect vaccination in the viral dynamics of SARS-CoV-2 in humans. As mentioned in "Introduction", several vaccines are being administered with different degrees of success. For instance, mRNA-1273, BNT162b2, Sputnik V, Ad26.COV2.S, Covishield, AZD1222 etc are showing promising results to reduce the burden of COVID-19. A vaccine is a biological preparation that provides active acquired immunity to a particular infectious agent. Thus if an individual is vaccinated, there will be no delay in the development of antibody. For simplicity, assume that the person is vaccinated a sufficiently large time ago so that the body develops antibodies against SARS-CoV-2. Further, let me assume that the person is fully vaccinated as most of the vaccines come with two doses. Therefore, the delay term $\tau$ is taken to be zero for vaccinated individuals (see Fig. 7). It is observed that vaccination not only reduces the viral load in healthy patients but also reduces the duration of high viremia.

Fig. 7

Viral load time series for different values of $\tau$ for the model (1). The fixed parameters are taken from Table 1 with $\mu _2 =0.65$, $k_2=5$, $\eta =0.05$ and $\tau =7$. Other fixed values are taken to be the average of estimated parameters for patient A and patient B

Overall, for antiviral drug target, blocking virus production is more fruitful in terms of viral load reduction and vaccination will also be effective.

Discussion and Conclusion

In this study, we have proposed and analyzed a compartmental model of SARS-CoV-2 transmission within the human body. The much needed innate and adaptive immune responses are incorporated into the model. The eight-dimensional model has four types of equilibrium points. The existence criterion for each type of equilibria is presented. From the local stability of the DFE, the expression for basic reproduction number is obtained. This number is very crucial for the persistence of the virus in the long run. However, the short-term dynamics of the viral load is studied using various numerical techniques. During time series analysis, we observed that the viral load time series experiences a peak between sixth and seven days post-infection, followed by a sharp decrease due to activation of adaptive immune response (see Fig. 2). A forward bifurcation of equilibria with respect to the basic reproduction number is observed and depicted in Fig. 3. This also ensures that if we suitably vary parameters involved in the expression of $R_0$, the same type of phenomenon occurs. Thus, in turn, parameters such as $\beta$ and $k_1$ can be decreased to reduce $R_0$ below unity and ensure local asymptotic stability of DFE.

We used daily measurements of SARS-CoV-2 viral load in sputum for two patients [44] from a hospital in Munich, Germany to estimate unknown model parameters. Using the estimated parameters, the global sensitivity analysis of several model parameters with respect to peak viral load is performed. The results indicate that the production rate of virus particles from infected cells will increase the chance of more significant infection propagation. Besides, the infection rate and the immunosuppresion rate will increase the peak of viral load. Additionally, the natural death rates of infected cells and the death rate of virus particles will have a significant negative correlation with the peak of viral load. The production rate of cytokines is also negatively correlated with the peak of viral load. These results reinforce the fact that $\beta$ and $k_1$ are very crucial for the reduction of viral load.

Antiviral drugs can be used to slow SARS-CoV-2 infection (or reduce $\beta$) or block the production of virus particles (or reduce $k_1$). Numerical simulations are performed to quantify the efficacy of antiviral drugs (see Fig. 6). It can be seen that increasing levels of efficacy in both targets reduce the viral load. Results suggest that a decrease in $\beta$ reduces the peak of viral load but the duration of the high viral load remains the same. On the other hand, a decrease in $k_1$ significantly reduces both peak of viral load and period of high viral load. Thus, we conclude that blocking virus production from infected cells is a more suitable target for antiviral drug development. Moreover, we simulate the model to quantify effect of vaccination on the viral load. Vaccination can reduce the viral load in healthy patients and also reduce the duration of high viremia in the body. Vaccinated persons show a significantly smaller period of high viral load than antiviral drugs (see Fig. 7). Thus, it can be argued that vaccination is more effective intervention as compared to the antiviral treatments employed here. The mathematical model developed in this paper can be improved by adding more detailed data to reveal prophylactic and therapeutic interventions. Our theoretical findings should be tested clinically for the implementation. Further insights into immunology and pathogenesis of SARS-CoV-2 will help to reduce the current pandemic.

Appendix A

See Table 2.

Table 2 Dataset used for calibrating the proposed model. Data is given in $log_{10}$ scale