Many attempts to build epidemic models of the current Covid-19 epidemic have been made in the recent past.

The relevance of mathematical models lies in their ability to describe and predict the evolution of the epidemic, with evident and positive consequences on the contagion containment; moreover, if the models match with the collected data, the biological hypotheses on which they are based can be validated.

So far, mostly SIR and SEIR models were used [1, 2]. In our opinion, these models have the defect of considering immunity from SARS-Cov-2 as permanent, while, on the basis of our knowledge on coronaviruses, immunity is highly probable to be only temporary, estimated between 6 and 12 months.

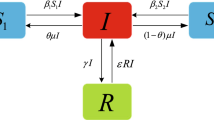
Due to these considerations, we reckoned that a SIRS (Susceptible, Infected, Recovered, Susceptible) model, sometimes also referred to as SI(R) (where the brackets around R indicate the transient state of the Recovered) is more suitable to describe this epidemic.

In other words, the model envisages a structure of this kind: at the beginning of the epidemic, there are only susceptible subjects (that is, without immunity) and no recovered (which means neither deceased nor healed). Upon the arrival of the first infected subject, the model evolves as follows: among the susceptible people, some become infected (passing from group S to group I) and, over time, some infected patients die while others heal (passing from group I to group R). In our model, moreover, we take into account the fact that, after a certain period of transitory immunity, the healed ones go back to being susceptible (that is, passing from group R to group S). Our interest is to predict a possible scenario when an equilibrium will be reached between the groups of Susceptible, Infected, and Recovered (which is what normally happens in epidemics).

The SI(R) model is described by the following ordinary differential system:

$$ \left\{\begin{array}{c}\frac{dS}{dt}=-\alpha S(t)I(t)+\rho R(t)\\ {}\frac{dI}{dt}=\alpha S(t)I(t)-\beta I(t)\\ {}\frac{dR}{dt}=\beta I(t)-\rho R(t)\end{array}\right. $$
(1)

where S, I, R are the proportions of Susceptible, Infected, and Recovered in the population, respectively, so that S + I + R = 1 at each time; α is the infection rate parameter; β is the removal rate parameter; and ρ is the rate of loss of immunization.

One of the most interesting aspects of model (1) is that it offers an analytical solution to the problem of finding possible steady states, resulting in the following (positive) endemic equilibrium (under the realistic condition that \( \frac{\beta }{\alpha }<1 \)):

$$ {S}_{\ast }=\frac{\beta }{\alpha } $$
(2)
$$ {I}_{\ast }=\frac{\rho }{\alpha}\frac{\alpha -\beta }{\beta +\rho } $$
(3)
$$ {R}_{\ast }=\frac{\beta }{\rho }{I}_{\ast } $$
(4)

Parameters β and ρ can be estimated biologically: β is the reciprocal of the average period of infection and can therefore be estimated to be about 0.1; ρ is the reciprocal of the duration of the presumed immunity and can be estimated as ranging from 0.003 to 0.006 (t is expressed in days) [3].

The infection rate α was estimated under the hypothesis, based on real Italian data, that the epidemic peak is reached around 21 days after the lockdown; this hypothesis led to estimate α in 0.6.

However, it should be borne in mind the problem of the high percentage of infected, but asymptomatic, subjects, a fact which is highlighted by many evidences. In particular, the proportion p of symptomatic subjects (i.e. the fraction of infective individuals identified by diagnosis) in the infected population is currently estimated to be in the range 0.01 to 0.10 [2, 4].

From the above considerations, we have calculated the proportions of the compartments (i.e. the subpopulations) S, I, R at the steady state (i.e. at the equilibrium), obtaining the impressive proportion of Susceptible S∗ = 0.17.

In practical terms, this means that equilibrium is reached when almost all of the population (83%) will not be susceptible to infection anymore, because either currently infected or still immune, due to a recent healing.

Note that the value of S∗, due to (2), does not depend on the value of ρ. On the contrary, the values of I∗ and R∗ do depend on ρ; their estimates are shown in Table 1. An example of the evolution of a SI(R) model, obtained according to the parameter estimates proposed in our model, is shown in Fig. 1.

Table 1 Proportions of Susceptible, Infected, and Recovered at the steady state
Full size table
Fig. 1
figure 1

Evolution of a SI(R) model according to the parameter estimates proposed. For a better comprehension, both the Recovered (R) and the Infected (I) subpopulations are subdivided into Symptomatic and Asymptomatic subjects (ratio 1:9). S indicates the Susceptible subpopulation

Full size image

Therefore, at the steady state, a substantially endemic situation of Infected included between 0.02 and 0.04, and a proportion of Recovered (i.e. deceased and healed) included between 0.79 and 0.81 should be expected.

However, it is crucial to remember that the results concerning the Recovered, which at first glance are particularly impressive, include the huge proportion of asymptomatic subjects, which, as mentioned above, is estimated to be between 90 and 99% of the Infected.

Finally, it is appropriate to analyse in more detail the result of the Recovered at the equilibrium. Among these, the deceased are indicatively 1–3%, while the asymptomatic ones are included between 90 and 99%.

We tried to apply these results to the updated data concerning Marche region (Central Italy) and the province of Pesaro-Urbino (a province of Marche region, one of the main outbreaks of the epidemic in Italy). In Marche, the current proportion (data collected on day April 15, 2020) of Susceptible varies between 0.48 and 0.95 (taking into account a proportion of asymptomatic subjects equal to 1 − p = 0.99 and 1 − p = 0.90 respectively), while in the province of Pesaro-Urbino, it varies between 0.20 and 0.92.

In these estimates, the proportion of Susceptible S is calculated according to the following formula:

$$ S=1-\frac{I+R}{p} $$
(5)

We have also calculated the current situation of the Susceptible for the province of Hubei, the Chinese region where the pandemic originated; this proportion varies between 0.72 and 0.97 (i.e. it is similar to that of Marche region). Hence, compared with the Marche and Hubei regions, the situation in the province of Pesaro-Urbino appears closer to equilibrium.

However, in this analysis, we must not forget that the α parameter (i.e. the infection rate) affects S∗, according to (2).

This parameter depends on many factors: (a) the biological characteristics of the virus’s contagiousness; (b) the pattern of social contacts that reflects the family and social structures of a nation [5]; (c) the containment policy to oppose the spread of the virus (such as the lockdown implemented by many governments all over the world).

Obviously, neither the first nor the second factors can be modified. On the contrary, the containment policy can induce a decisive impact. The lockdown set up for some outbreaks of infection around the world can drastically lower the α parameter, with obvious consequences on the proportion of Susceptible at the equilibrium. Obviously, right now we do not know how the α parameter will vary at the end of the lockdown and if there will be variations of the epidemic according to seasonality.

This model can therefore help to guide public health choices. It also stresses the importance of estimating the percentage of asymptomatic, in order to predict how long it is until the decisive achievement of the state of equilibrium. To do this, however, the model needs to be validated; this validation requires the use of reliable statistical data, while, at the moment, they appear extremely unreliable and not comparable among different countries. Hence, it is necessary to raise awareness both in public health institutions, in order to monitor the quality of data, and in clinicians, to point out the usefulness of these models.