Introduction

The novel coronavirus SARS-CoV-2 (COVID-19) is a spreadable disease that may be spread through contact and droplets1,2,3. The symptoms and signs of COVID-19 disease are visible after roughly 5.2 days (development period)4. The primary and common symptoms are fever, cough, fatigue, and sore throat, followed by other symptoms such as headache, diarrhea, the inability to sense taste and smell, muscle pain etc.4,5. In critical cases, infected people may develop bronchitis, pneumonia, severe acute respiratory distress syndrome (SARDS), multi-organ failure, and these may lead to death. In December 2019, the Wuhan city in China reported the first confirmed COVID-19 case; since then, the virus has spread universally. On March 11th, 2020, the World Health Organization (WHO) announced the COVID-19 epidemic as a pandemic6. The reported cases of COVID-19 have since been risen exponentially around the world reaching more than 200 nations7. As of September 11, 2020, the total number of infected cases is 28,316,605 and the total number of deaths is 913,284 all over the world8.

Nowadays mathematical modeling has been well recognized as an epidemiological tool to combat many infectious diseases. Many researchers attempted to study and model infectious diseases which is an interdisciplinary field where biological knowledge of epidemics is equally important along with the mathematical framework. The very first epidemiological mathematical model was traced back to the findings of Daniel Bernoulli in the eighteenth century to estimate the life expectancy in smallpox epidemics9. Ross constructed a set of mathematical equations to demonstrate the transmission of malaria parasites between mosquitoes and humans10. The Macdonald11 modified the work of Ross10 later and named it as well-known Ross-Macdonald models. The law of mass action was integrated into the Ross model by Kermack and McKendrick and new compartmental models were introduced12. These models later became the most extensively used basic structures usually called compartment models in infectious disease modeling. In the conventional compartmental model, the entire population is split into compartments according to the health status of people such as susceptible to being healthy individuals (S), infectious individuals (I), and recovered individuals (R) as in the SIR model13. The models’ SI, SIS, SIRS, SEIR (E-exposed but not infectious), SEIRS, MSIR (M-maternal immunity), MSEIR, and MSEIRS are other types of compartmental models that have been applied to many evolving communicable diseases like influenza and Ebola14,15.

Recently, Anastapoulou et al. proposed the SIR model for predicting COVID-19 outbreak16. Casella constructed a controlled SIR compartment model that includes the effect of delays and the outcome of different control strategies17. Giordano et al. developed a model called the SIDARTHE model that forecasts the effective control strategy of the COVID-19 pandemic situation in Italy18. It consists of eight classes such as susceptible (S), infected (I), diagnosed (D), ailing (A), recognized (R), threatened (T), healed (H) and extinct(E). The model differentiates between detected and non-detected among the infected cases and between life-threatening and non-life-threatening cases. Effect of lockdown, the effect of testing etc. were simulated. The research results established that social-distancing, an adequate number of tests and contact tracing will help to reduce the COVID-19 pandemic.

Researchers from Portugal and Spain proposed an ad-hoc compartmental model for COVID-19 in Wuhan19. In addition to categories such as susceptible, exposed, symptomatic, asymptomatic, and recovery, the research considered classes of individuals based on fatality, hospitalization, and super-spreaders. The basic reproduction number was computed to be 0.945, less than 1. So, the disease-free equilibrium was found to be stable. The sensitivity index of each of the parameters was calculated and the model was compared with the real data sets. The predicted model fits with the actual data of daily confirmed deaths.

The impact of social distancing and lockdown measures were studied in the research20 where a compartmental SEIR model was proposed. The research recommended that the total cases can be reduced by 90% if proper countermeasures are carried out. The dynamic behavior of the disease is studied in21 by developing a mathematical model by including isolation class. As per the research findings, the main cause of the disease spread is the contact between people. So, isolation of infected people is highly recommended to reduce the spread.

In this work, we suggest a new compartmental model that extends the classical SIR model by incorporating various infectious stage of the COVID-19 epidemic in the Sultanate of Oman for 145 days. As of September 11, 2020, out of 88,337 confirmed cases in the Sultanate of Oman, 4250 are active, 83,325 have recovered, and 762 are dead8.

Materials and methods

In this research, we formulate the transmission mechanism of COVID-19 using a compartmental model which is deterministic in nature. We have collected patient wise demographic data including symptoms from Royal hospital, Oman after taking formal ethical approval. The data highlighted the number of patients admitted in ICU, admitted in the hospital, and not required admission in the hospital. Their duration of stay in the hospital (1 to 30 days) is also given in the data depending on the severity of the disease. Also, we have studied various symptoms, along with the severity of the diseases which leads to arrive at different compartments. We have made a detailed study on the various stages from mild to severe that COVID-19 patient is undergoing while they are under treatment. These studies prompted us to make a compartment model that incorporates mild, moderate, critical, and severe cases separately instead of taking all together as an infected case.

To formulate the mathematical model, the total population is grouped into eight mutually exclusive compartments based on their disease status. The class of Susceptible individuals (S) are those who have never been infected with and thus have no immunity against COVID-19. Susceptible individuals become exposed once they are infected with the disease. The Exposed individuals (E) are those who are in the infected stage, but not yet infectious to others. The class (A) of infected individuals are those with no symptom or mild symptom developed. These individuals may have symptoms like fever and cough but with normal chest X-ray result. These individuals may either improve or progress to the Moderate stage of the disease. The Moderate class (M) of individuals suffers from a moderate infection symptom like fever and cough and may even have mild pneumonia but do not need hospitalization. In this stage, they are likely to show symptoms of fever and cough and with chest X-ray result that indicate major bilateral abnormality, pneumonia, or infiltrations/patchy shadowing. These individuals may either improve or progress to the severe stage of the disease.

The hospitalized individuals (H) suffer from a severe infection and have severe pneumonia and need hospitalization. These people show indications of serious pneumonia that prompts dyspnea, blood oxygen saturation that is less than or equal to 93%, respiratory frequency which is more than or equivalent to 30 breaths/min at rest, the ratio of the partial pressure of arterial oxygen to fraction of inspired oxygen being less than or equal to 300 mmHg, and/or lung infiltration that is more than 50% within 24 to 48 hours. Such cases require immediate hospitalization and supplemental oxygen. These individuals may either recover or progress to the critical stage of the disease. The class of critical (C) individuals are affected by a critical infection like a failure in the respiratory system, septic shock, and/or dysfunction in multiple organs and require treatment in an Intensive care unit (ICU), often with the requirement of mechanical ventilation. These individuals may either recover or die suffering from the disease during the time. The Recovered individuals (R) are those who have recovered and are expected to be immune to future infection with COVID-19. The class of individuals (D) are those who have died because of COVID-19. Depending on the severity of diseases like mild, moderate, severe, and critical, the Infected people are sent to appropriate COVID care centers or at home isolation. The authorities are monitoring their progress daily and taking appropriate actions22.

Model and equations

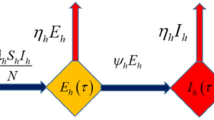
Figure 1 depicts the various stages of the proposed compartment model.

Figure 1
figure 1

The different stages of the compartment model.

Full size image

At any time, t, total population N (t) = S (t) + E (t) + A(t) + M (t) + H(t) + C (t) + R(t) + D(t). These 8 compartments are governed by 8 dynamic system of non-linear differential equations that vary with time, and nature of the solution and the stability of the system is investigated. Figure 2 depicts the diagram of the overview of the model. The corresponding equations and the description of the various parameters involved are given in Eq. (1). The compartment C is completely isolated to strict preventive measures and proper care in ICU. Hence the transmission from C is considered as negligibly small.

$$S^{\prime}(t) = - S(t)\left[ {\beta A(t) + \gamma M(t) + \delta H(t)} \right]$$
$$E^{\prime}(t) = S(t)\left[ {\beta A(t) + \gamma M(t) + \delta H(t)} \right] - \lambda (\theta_{1} + \theta_{2} + \theta_{3} )E(t)$$
$$A^{\prime}(t) = \lambda \theta_{1} E(t) - \left( {\sigma + r_{1} } \right)A(t)$$
$$M^{\prime}(t) = \lambda \theta_{2} E(t) + \sigma A(t) - \left( {\mu + r_{2} } \right)M(t)$$
(1)
$$H^{\prime}(t) = \lambda \theta_{3} E(t) + \mu M(t) - \left( {\rho + r_{3} } \right)H(t)$$
$$C^{\prime}(t) = \rho H(t) - (\tau + r_{4} )C(t)$$
$$R^{\prime}(t) = r_{1} A(t) + r_{2} M(t) + r_{3} H(t) + r_{4} C(t)$$
$$D^{\prime}(t) = \tau C(t)$$
Figure 2
figure 2

The overview of the model.

Full size image

We choose \(\theta_{3} = 1 - (\theta_{1} + \theta_{2} )\).

Table 1 provides the description the parameter.

Table 1 Description of the parameter.
Full size table

Analysis of the model

Nonnegativity of solutions

The model (1) represents a bilinear system consists of 8 differential equations. The system is considered positive when all the compartmental variables assume non-negative values for \(t \ge 0\). \(R(t)\) and \(D(t)\) are cumulative variables.

Proposition 1

Consider a system F(t) = (S, E, A, M, H, C, R, D) with the initial conditions \(F(0) \ge 0\), then the solutions of (1) are non-negative for all \(t \ge 0\).

Proof

The integrating factor of first equation in (1) is \(e^{{\int\limits_{0}^{t} {\left( {\beta A(\phi ) + \gamma M(\phi ) + \delta H(\phi } \right))d\phi } }}\).

So, the solution is \(S(t){\kern 1pt} {\kern 1pt} e^{{\int\limits_{0}^{t} {\left( {\beta A(\phi ) + \gamma M(\phi ) + \delta H(\phi } \right))d\phi } }} = S(0)\)

$$S(t){\kern 1pt} = S(0){\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {e^{{ - \int\limits_{0}^{t} {\left( {\beta A(\phi ) + \gamma M(\phi ) + \delta H(\phi } \right))d\phi } }} } \right) \ge 0$$

Similarly, we can establish other variables also. Thus \(F\left( t \right) \ge 0\) for all \(t \ge 0\).

The compartmental system satisfies mass conservative property, and it can be verified easily from (1) that \(S^{\prime}(t) + E^{\prime}(t) + A^{\prime}(t) + M^{\prime}(t) + H^{\prime}(t) + C^{\prime}(t) + R^{\prime}(t) + D^{\prime}(t) = 0\). Hence the total population is a constant. When we consider each variable as the fraction of population, we can assume \(S(t) + E(t) + A(t) + M(t) + H(t) + C(t) + R(t) + D(t) = 1\), where 1 represents the total population.

Assuming an initial condition \(S(0)\), \(E(0)\), \(A(0)\),\(M(0)\), \(H(0)\), \(C(0)\), \(R(0)\), \(D(0)\) summing to 1, it is possible to prove that the variables converge to an equilibrium \(\overline{S} \ge 0\), \(\overline{E} = 0\), \(\overline{A} = 0\),\(\overline{M} = 0\), \(\overline{H} = 0\), \(\overline{C} = 0\), \(\overline{R} \ge 0\), \(\overline{D} \ge 0\) with \(\overline{S} + \overline{R} + \overline{D} = 1\). So only the susceptible, recovered and dead populations are eventually present. This means that the epidemic phenomenon has come to an end. All the possible equilibria are given by \((\overline{S},0,0,0,0,0,\overline{R},\overline{D})\) with \(\overline{S} + \overline{R} + \overline{D} = 1\). In our model (1) the rate of the transmission parameter values \(\beta ,\gamma\) is to be reduced by strict social measures. Also, the rate of the main transition parameters \(\sigma\),\(\mu\) depends on the strictness of the home isolation and quarantine process. Even if the strict procedure is adopted in hospital admission, there is always a chance for the disease to spread from the hospital. This is because long-time exposure to huge numbers of infected patients directly increments the risk of infection among healthcare workers. In addition to this, inadequate personal protection of healthcare workers, shortage of personal protective equipment (PPE), as well as lack of organized training, practice, professional administration, and guidance also may aid the spread the disease. The increase in awareness of personal protection, availability of sufficient personal protection equipment (PPE), and proper awareness would play a significant role in reducing the risk of infection among healthcare workers23. Hence by considering all these factors, we incorporated compartment class H in our model in determining the spread of the disease, specifically in calculating the basic reproduction number.

The model has mainly three subsystems: The first subsystem is the susceptible individuals (S), the second subsystem is the infected and exposed individuals (\(E\), \(A\), \(M\), \(H\), \(C\)) which are non-zero in the transmission state , the third subsystem includes the recovered and removed individuals (\(R\),\(D\)). The second subsystem is more important in the epidemic study. When this subsystem is zero the remaining variables are at equilibrium. The variables \(R\), \(D\), are monotonically increasing and converge to the values \(\overline{R}\), \(\overline{D}\), respectively and \(S\) is monotonically decreasing and converges to \(\overline{S}\) if and only if the second subsystem converges to zero.

Basic reproduction number (R0)

It is not possible to predict the endemicity of the disease based on the increase or decrease in the number of cases alone. We need to find equilibria and linearization about each equilibrium to determine whether the disease is pandemic or not. If an equilibrium is unstable with all susceptible population, then it is an epidemic, and if it is asymptotically stable, then it is the end of the pandemic. To get a meaningful realization of the situation, the basic reproduction number (R0) is calculated, and this determines whether there is an epidemic or not. The basic reproduction number (R0) is debatably the most significant quantity in infectious disease epidemiology. It is among the quantities most critically evaluated for evolving infectious diseases in epidemic states, and its value delivers insight when scheduling control interventions for conventional infections. It can be found easily whether the disease-free equilibrium of the system exists and is calculated from this system of the equation after converting to next-generation matrix (NGM).

If R0 < 1, the infection stops, and if R0 > 1, there is an epidemic. The basic reproduction number (R0) is characterized as the number of secondary diseases brought about by a single infected individual from a susceptible population and is an indicator of the severity of the disease. Diekmann et al.1 and Van den Driessche and Watmough2 proposed a generalized approach to determine the basic reproduction number using the next generation matrix approach. The linearization of (1) the disease-free equilibrium is of the form \((\overline{S},0,0,0,0,0,\overline{R},\overline{D})\). The infectious sub-system from (1) can be written as

$$E^{\prime}(t) = S(t)\left[ {\beta A(t) + \gamma M(t) + \delta H(t)} \right] - \lambda (\theta_{1} + \theta_{2} + \theta_{3} )E(t)$$
$$A^{\prime}(t) = \lambda \theta_{1} E(t) - \left( {\sigma + r_{1} } \right)A(t)$$
$$M^{\prime}(t) = \lambda \theta_{2} E(t) + \sigma A(t) - \left( {\mu + r_{2} } \right)M(t)$$
(2)
$$H^{\prime}(t) = \lambda \theta_{3} E(t) + \mu M(t) - \left( {\rho + r_{3} } \right)H(t)$$

The Jacobian matrix from (2) is

$$J_{I} = \left[ {\begin{array}{*{20}c} { - p_{1} } & \beta & \gamma & \delta \\ {{\lambda}\theta_{1} } & { - p_{2} } & 0 & 0 \\ {{\lambda}\theta_{2} } & \sigma & { - p_{3} } & 0 \\ {{\lambda}\theta_{3} } & 0 & \mu & { - p_{4} } \\ \end{array} } \right]$$

where \(p_{1} = \lambda \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) = \lambda\), \(p_{2} = \sigma + r_{1}\), \(p_{3} = \mu + r_{2}\), \(p_{4} = \rho + r_{3}\),

Now the Jacobian matrix is decomposed into two matrices (transmission matrix and Transition matrix).

\(T = \left[ {\begin{array}{*{20}c} 0 & \beta & \gamma & \delta \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]\) \(\Sigma = \left[ {\begin{array}{*{20}c} { - p_{1} } & 0 & 0 & 0 \\ {\lambda \theta_{1} } & { - p_{2} } & 0 & 0 \\ {\lambda \theta_{2} } & \sigma & { - p_{3} } & 0 \\ {\lambda \theta_{3} } & 0 & \mu & { - p_{4} } \\ \end{array} } \right]\) The NGM with classical domain is denoted by DC. Here, we assume an auxiliary matrix E of K is of the form: \(K = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]\).

Now.

\(D_{C} = - K^{\prime}T\Sigma^{ - 1} K = \left[ {\begin{array}{*{20}c} {\frac{{\beta \theta_{1} }}{{p_{2} }} + \frac{{\gamma \sigma \theta_{1} }}{{p_{2} p_{3} }} + \frac{{\gamma \theta_{2} }}{{p_{3} }} + \frac{{\delta \sigma \mu \theta_{1} }}{{p_{2} p_{3} p_{4} }} + \frac{{\delta \mu \theta_{2} }}{{p_{3} p_{4} }} + \frac{{\delta \theta_{3} }}{{p_{4} }}} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]\).

From this, the basic reproduction number by considering the classical domain matrix is the spectral radius of the NGM.

$$R_{0} = trace(D_{C} ) = \frac{{\beta \theta_{1} }}{{p_{2} }} + \frac{{\gamma \theta_{2} }}{{p_{3} }} + \frac{{\delta \theta_{3} }}{{p_{4} }} + \frac{{\gamma \sigma \theta_{1} }}{{p_{2} p_{3} }} + \frac{{\delta \mu \theta_{2} }}{{p_{3} p_{4} }} + \frac{{\delta \sigma \mu \theta_{1} }}{{p_{2} p_{3} p_{4} }}$$
(3)

Steady state analysis

Proposition 2

The disease-free equilibrium is unstable for \(R_{0} > 1\) , and stable for \(R_{0} < 1\).

Proof

The dynamical matrix of the linearized system around the equilibrium \((\overline{S},0,0,0,0,0,\overline{R},\overline{D})\) is.

$$J = \left[ {\begin{array}{*{20}c} 0 & 0 & { - \beta \overline{S}} & { - \gamma \overline{S}} & { - \delta \overline{S}} & 0 & 0 & 0 \\ 0 & {p_{1} } & {\beta \overline{S}} & {\gamma \overline{S}} & {\delta \overline{S}} & 0 & 0 & 0 \\ 0 & {\lambda \theta_{1} } & { - p_{2} } & 0 & 0 & 0 & 0 & 0 \\ 0 & {\lambda \theta_{2} } & \sigma & { - p_{3} } & 0 & 0 & 0 & 0 \\ 0 & {\lambda \theta_{3} } & 0 & \mu & { - p_{4} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \rho & { - p_{5} } & 0 & 0 \\ 0 & 0 & {r_{1} } & {r_{2} } & {r_{3} } & {r_{4} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \tau & 0 & 0 \\ \end{array} } \right]$$
(4)

The matrix (4) has three null eigenvalues and five eigenvalues which are the roots of the equation.

$$\begin{aligned} P(s) & \equiv \frac{{\beta \lambda \theta_{1} }}{{\left( {s + p_{1} } \right)\left( {s + p_{2} } \right)}} + \frac{{\gamma \sigma \lambda \theta_{1} }}{{\left( {s + p_{1} } \right)\left( {s + p_{2} } \right)\left( {s + p_{3} } \right)}} + \frac{{\gamma \lambda \theta_{2} }}{{\left( {s + p_{1} } \right)\left( {s + p_{3} } \right)}} \\ & \quad + \frac{{\delta \sigma \mu \lambda \theta_{1} }}{{(s + p_{1} )(s + p_{2} )(s + p_{3} )(s + p_{4} )}} + \frac{{\delta \mu \lambda \theta_{2} }}{{(s + p_{1} )(s + p_{3} )(s + p_{4} )}} + \frac{{\delta \lambda \theta_{3} }}{{(s + p_{1} )(s + p_{4} )}} - 1 = 0 \\ \end{aligned}$$

Then \(P(0) = R_{0} - 1\), because \(p_{1} = \lambda \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) = \lambda\).

Now consider the following cases

Case 1

Suppose \(R_{0} > 1\). Then \(P(0) > 0\). Also \(P(s) \to - 1\) as \(s \to \infty\). Since \(P(s)\) is a continuous function of \(s\), hence by Bolzano theorem on continuous function implies that \(P(s_{i} ) = 0\) for some \(s_{i} > 0\), at least one eigenvalue must be positive. So, in this case, the equilibrium is unstable.

Case II

Suppose \(R_{0} < 1\). Then \(P(0) < 0\).

Assume that \(P(s) = 0\) has a root of the form \(x + iy\) where \(x,y \in R\) and \(x \ge 0\). Then \(P(x + iy) = 0\).

Now

$$\begin{aligned} \left| {P(x + iy) + 1} \right| & \le \frac{{\beta \lambda \theta_{1} }}{{\left| {\left( {s + p_{1} } \right)} \right|\left| {\left( {s + p_{2} } \right)} \right|}} + \frac{{\gamma \sigma \lambda \theta_{1} }}{{\left| {\left( {s + p_{1} } \right)} \right|\left| {\left( {s + p_{2} } \right)} \right|\left| {\left( {s + p_{3} } \right)} \right|}} + \frac{{\gamma \lambda \theta_{2} }}{{\left| {\left( {s + p_{1} } \right)} \right|\left| {\left( {s + p_{3} } \right)} \right|}} \\ & \quad + \frac{{\delta \sigma \mu \lambda \theta_{1} }}{{\left| {(s + p_{1} )} \right|\left| {(s + p_{2} )} \right|\left| {(s + p_{3} )} \right|\left| {(s + p_{4} )} \right|}} + \frac{{\delta \mu \lambda \theta_{2} }}{{\left| {(s + p_{1} )} \right|\left| {(s + p_{3} )} \right|\left| {(s + p_{4} )} \right|}} + \frac{{\delta \lambda \theta_{3} }}{{\left| {(s + p_{1} )} \right|\left| {(s + p_{4} )} \right|}} \\ & \quad \le \frac{{\beta \lambda \theta_{1} }}{{\left( {x + p_{1} } \right)\left( {x + p_{2} } \right)}} + \frac{{\gamma \sigma \lambda \theta_{1} }}{{\left( {x + p_{1} } \right)\left( {x + p_{2} } \right)\left( {x + p_{3} } \right)}} + \frac{{\gamma \lambda \theta_{2} }}{{\left( {x + p_{1} } \right)\left( {x + p_{3} } \right)}} \\ & \quad + \frac{{\delta \sigma \mu \lambda \theta_{1} }}{{(x + p_{1} )(x + p_{2} )(x + p_{3} )(x + p_{4} )}} + \frac{{\delta \mu \lambda \theta_{2} }}{{(x + p_{1} )(x + p_{3} )(x + p_{4} )}} + \frac{{\delta \lambda \theta_{3} }}{{(x + p_{1} )(x + p_{4} )}} \\ & \quad \le \frac{{\beta \lambda \theta_{1} }}{{p_{1} p_{2} }} + \frac{{\gamma \sigma \lambda \theta_{1} }}{{p_{1} p_{2} p_{3} }} + \frac{{\gamma \lambda \theta_{2} }}{{p_{1} p_{3} }} + \frac{{\delta \sigma \mu \lambda \theta_{1} }}{{p_{1} p_{2} p_{3} p_{4} }} + \frac{{\delta \mu \lambda \theta_{2} }}{{p_{1} p_{3} p_{4} }} + \frac{{\delta \lambda \theta_{3} }}{{p_{1} p_{4} }} = R_{0} < 1 \\ \end{aligned}$$

This shows \(1 < 1\), clearly a contradiction. Hence all roots of the equation \(P(s) = 0\) have the form \(x + iy\) where \(x,y \in R\) and \(x < 0\). Thus, all eigenvalues of the coefficient matrix have negative real part and this case equilibrium is stable, the solution of (1) die out exponentially9.

Final pandemic size relations

Proposition 3

The limit values \(\overline{S} = \mathop {\lim }\limits_{t \to \infty } S(t)\) , \(\overline{R} = \mathop {\lim }\limits_{t \to \infty } R(t)\) and \(\overline{D} = \mathop {\lim }\limits_{t \to \infty } D(t)\) or positive initial conditions, are given by.

$$l_{0} + R_{0} \left( {S(0) - \overline{S}} \right) = \log \left( {\frac{S(0)}{{\overline{S}}}} \right)$$
(5)
$$\overline{R} = R(0) + l_{R} + R_{R} \left( {S(0) - \overline{S}} \right)$$
(6)
$$\overline{D} = D(0) + f_{D} + R_{D} \left( {S(0) - \overline{S}} \right)$$
(7)

where \(l_{0} = - a^{T} B^{ - 1} x(0)\) , \(l_{R} = - b^{T} B^{ - 1} x(0)\), \(R_{R} = - b^{T} B^{ - 1} D\), \(l_{D} = - c^{T} B^{ - 1} x(0)\) and \(R_{D} = - c^{T} B^{ - 1} D\).

Proof

Define \(x = [E,A,M,H,C]^{T}\), we can write the subsystem as.

$$x^{\prime}(t) = B{\kern 1pt} x(t) + D{\kern 1pt} u(t) = \left[ {\begin{array}{*{20}c} { - p_{1} } & 0 & 0 & 0 & 0 \\ {\lambda \theta_{1} } & { - p_{2} } & 0 & 0 & 0 \\ {\lambda \theta_{2} } & \sigma & { - p_{3} } & 0 & 0 \\ {\lambda \theta_{3} } & 0 & \mu & { - p_{4} } & 0 \\ 0 & 0 & 0 & \rho & { - p_{5} } \\ \end{array} } \right]x(t) + \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]u(t)$$
(8)
$$y_{S} (t) = a^{T} x(t) = \left[ {\begin{array}{*{20}c} 0 & \beta & \gamma & \delta & 0 \\ \end{array} } \right]x(t)$$
(9)
$$y_{R} (t) = b^{T} x(t) = \left[ {\begin{array}{*{20}c} 0 & {r_{1} } & {r_{2} } & {r_{3} } & {r_{4} } \\ \end{array} } \right]x(t)$$
(10)
$$y_{D} (t) = c^{T} x(t) = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & \tau \\ \end{array} } \right]x(t)$$
(11)
$$u(t) = S(t)y_{S} (t)$$
(12)

where \(p_{1} = \lambda (\theta_{1} + \theta_{2} + \theta_{3} )\), \(p_{2} = \sigma + r_{1}\), \(p_{3} = \mu + r_{2}\), \(p_{4} = \rho + r_{3}\), \(p_{5} = \tau + r_{4}\).

and the other variables in the differential Eq. (1) can be written as

$$S^{\prime}(t) = - S(t){\kern 1pt} {\kern 1pt} y_{S} (t)$$
(13)
$$R^{\prime}(t) = {\kern 1pt} {\kern 1pt} y_{R} (t)$$
(14)
$$D^{\prime}(t) = {\kern 1pt} y_{D} (t)$$
(15)

The number of infectives always approaches zero and the number of susceptible always approaches a positive limit as \(t \to \infty\).

From (8)

$$\begin{gathered} S^{\prime}(t) = - S(t){\kern 1pt} {\kern 1pt} y_{S} (t) \hfill \\ - \frac{S^{\prime}(t)}{{S(t){\kern 1pt} }} = {\kern 1pt} y_{S} (t) \Rightarrow - \int\limits_{0}^{\infty } {\frac{S^{\prime}(t)}{{S(t){\kern 1pt} }}} = \int\limits_{0}^{\infty } {{\kern 1pt} y_{S} (t)} \hfill \\ \Rightarrow \int\limits_{0}^{\infty } {{\kern 1pt} y_{S} (t)} = \log \left( {\frac{S(0)}{{\overline{S}}}} \right) \hfill \\ \end{gathered}$$
(16)

From (7)

$$\begin{gathered} \int\limits_{0}^{\infty } {x^{\prime}(\phi )d\phi } = B\int\limits_{0}^{\infty } {{\kern 1pt} x(\phi )} d\phi + D\int\limits_{0}^{\infty } {{\kern 1pt} u(\phi )d\phi } \hfill \\ x(\infty ) - x(0) = B\int\limits_{0}^{\infty } {{\kern 1pt} x(\phi )} d\phi + D\int\limits_{0}^{\infty } {{\kern 1pt} S(\phi )y_{S} (\phi )d\phi } \hfill \\ \end{gathered}$$

from (12).

Since \(x(\infty ) = 0\)

$$- x(0) = B\int\limits_{0}^{\infty } {{\kern 1pt} x(\phi )} d\phi - D\int\limits_{0}^{\infty } {{\kern 1pt} S^{\prime}(\phi )d\phi }$$

from (13)

$$- x(0) = B\int\limits_{0}^{\infty } {{\kern 1pt} x(\phi )} d\phi - D\left( {\overline{S} - S(0)} \right)$$
(17)

Pre multiply by \(a^{T} B^{ - 1}\) and using (9) we have

$$- a^{T} B^{ - 1} x(0) = a^{T} B^{ - 1} B\int\limits_{0}^{\infty } {{\kern 1pt} x(\phi )} d\phi - a^{T} B^{ - 1} D\left( {\overline{S} - S(0)} \right)$$
$$- a^{T} B^{ - 1} x(0) = \int\limits_{0}^{\infty } {{\kern 1pt} y_{S} (\phi )} d\phi - a^{T} B^{ - 1} D\left( {\overline{S} - S(0)} \right)$$
$$l_{0} = \log \left( {\frac{S(0)}{{\overline{S}}}} \right) + R_{0} \left( {\overline{S} - S(0)} \right)$$

from (16)

where \(l_{0} = - a^{T} B^{ - 1} x(0)\) and it is easy to show that \(R_{0} = - a^{T} B^{ - 1} D\). So

$$l_{0} + R_{0} \left( {S(0) - \overline{S}} \right) = \log \left( {\frac{S(0)}{{\overline{S}}}} \right)$$

The expressions (6) and (7) can be proved easily by pre-multiplying (17) by \(b^{T} B^{ - 1}\) and \(c^{T} B^{ - 1}\) respectively.

Note that with an initial condition \([E(0) > 0,A(0) = M(0) = H(0) = C(0) = 0]\),we can compute \(l_{0}\) as \(l_{0} = R_{0} E(0)\) and for long term prediction it has to be adjusted by considering \(l_{0} = - a^{T} B^{ - 1} x(t_{0} )\) where B includes new parameter values. In (5) also, it is adjusted accordingly by \(S(t_{0} )\).

Extension of the model by including exposed period

The study on COVID-19 reveals the fact that transmission of disease happens in various stages, namely symptomatic transmission, pre-symptomatic transmission, and asymptomatic transmission. In the case of a symptomatic transmission, the infected persons develop signs and symptoms compatible with COVID-19 virus infection and transfers to the contacted person(s). Specifically, symptomatic transmission denotes the transmission from a person while they are suffering from the symptoms and this transmission takes place through respiratory droplets or by contact with the contaminated objects and surfaces5,30,31,32,33,34. Research studies on virus infection reveal that flaking of COVID-19 virus is peak in the upper respiratory tract (nose and throat) early during the disease, which is, within the first three days from the start of symptoms24,25,26. Preliminary data proposes that people may be more infectious around the time of the beginning of the symptoms as compared to the later stages of the disease35,36,37.

In the case of pre-symptomatic transmission, there is an incubation period (on average 5–6 days and can be extended up to 14 days) which is the duration between the first day of infection and symptom onset, is, however, can be up to 14 days. During this period, some infected persons can be contagious. Therefore, transmission from a pre-symptomatic case can occur up to a certain extent before symptom onset. Various studies24,25,26,27,28,29 reveal that people can be tested positive for COVID-19 from 1 to 3 days before the development of symptoms. Thus, it is probable that infected people could transmit the disease before the onset of any visible symptoms. It is very significant to understand that pre-symptomatic transmission still needs the virus to be spread through infectious droplets or through touching contaminated surfaces.

While in asymptomatic transmission, a person is infected with COVID-19, but no visible symptoms. Asymptomatic transmission refers to the transmission of the infection from an infected individual who does not show any symptoms. Even though there is no solid report on asymptomatic transmission, we cannot avoid the possibility that it may occur. In some countries, asymptomatic cases have been reported through an effective contact tracing mechanism. WHO frequently monitors all evolving evidence about this and is delivering updates whenever more information becomes available. So in our model (1), the exposed classes are divided into two separate classes namely \(E_{N}\) defines no symptom or transmission and \(E_{T}\) with no symptom but can transmit the virus (“pre-symptomatic transmission”), based on the various studies24,25,26,27,28,29 about COVID-19 pre-symptomatic infection. The rate of exit from \(E_{N}\) is \(\varepsilon\) and from \(E_{T}\) is \(\upsilon\). Accordingly, the modified diagram by expanding exposed case is given in Fig. 3. The modified equation of (1) is also given in (18).

$$S^{\prime}(t) = - S(t)\left[ {\alpha E_{T} + \beta A(t) + \gamma M(t) + \delta H(t)} \right]$$
$$E_{N} ^{\prime}(t) = S(t)\left[ {\alpha E_{T} + \beta A(t) + \gamma M(t) + \delta H(t)} \right] - \varepsilon E_{N} (t)$$
$$E_{T} ^{\prime}(t) = \varepsilon E_{N} (t) - \upsilon (\theta_{1} + \theta_{2} + \theta_{3} )E_{T} (t)$$
$$A^{\prime}(t) = \upsilon \theta_{1} E{}_{T}(t) - \left( {\sigma + r_{1} } \right)A(t)$$
$$M^{\prime}(t) = \upsilon \theta_{2} E_{T} (t) + \sigma A(t) - \left( {\mu + r_{2} } \right)M(t)$$
(18)
$$H^{\prime}(t) = \upsilon \theta_{3} E_{T} (t) + \mu M(t) - \left( {\rho + r_{3} } \right)H(t)$$
$$C^{\prime}(t) = \rho H(t) - (\tau + r_{4} )C(t)$$
$$R^{\prime}(t) = r_{1} A(t) + r_{2} M(t) + r_{3} H(t) + r_{4} C(t)$$
$$D^{\prime}(t) = \tau C(t)$$
Figure 3
figure 3

Extension of the model by including exposed period.

Full size image

We choose \(\theta_{3} = 1 - (\theta_{1} + \theta_{2} )\).

Accordingly, the basic reproduction number using next generation matrix can be written as

$$R_{0} = \frac{\alpha }{{p_{1} }} + \frac{{\beta \theta_{1} }}{{p_{2} }} + \frac{{\gamma \theta_{2} }}{{p_{3} }} + \frac{{\delta \theta_{3} }}{{p_{4} }} + \frac{{\gamma \sigma \theta_{1} }}{{p_{2} p_{3} }} + \frac{{\delta \mu \theta_{2} }}{{p_{3} p_{4} }} + \frac{{\delta \sigma \mu \theta_{1} }}{{p_{2} p_{3} p_{4} }}$$
(19)

where \(p_{1} = \upsilon (\theta_{1} + \theta_{2} + \theta_{3} ) = \upsilon\), \(p_{2} = \sigma + r_{1}\), \(p_{3} = \mu + r_{2}\), \(p_{4} = \rho + r_{3}\), \(p_{5} = \tau + r_{4}\).

The model including exposed period was implemented in MATLAB and findings are depicted in “Results” section.

Results

The simulation of the extended model is implemented in MATLAB. The data for this study has been taken from the official Tarassud Plus application, Ministry of Health, Oman38 and the sources38,39. The data of Oman during the period June 4th, 2020 to July 30th, 2020 (about 57 days) has been used for this study. During this period, the country has undergone lockdown, partial lockdown and relaxation. The given data is categorized into 9 compartments (S, \(E_{N}\), \(E_{T}\),, A, M, H, C, R, D) as mentioned in the methodology Section 2.1. The data for the study is given in Table 2.

Table 2 Oman Dataset.
Full size table

We investigated the model parameters and corresponding effective reproduction number R0 during the period from June 4th to July 30th when the country has undergone various intervened measures to control the disease.

Parameter estimation

Mathematical models are useful in capturing patterns in data, thereby predicting the nature of a pandemic to take the right policy to control it. Hence it is very essential to find out the best-fit parameters that give the closest correspondence between model predictions and data. The parameter estimation is done based on parameterized nonlinear functions which solve the \(\min \left( {\sum {\left\| {F(x_{i} - y_{i} } \right\|^{2} } } \right),\) where \(F(x_{i} )\) is a nonlinear function and \({y}_{i}\) is data. The parameters for each period are chosen in such a way that it gives the minimum value for R0.

Figure 4 shows the R0 over a different period, and active cases versus R0. Figure 5 shows the various transmission parameters over a period from June to August based on the fitted data’.

Figure 4
figure 4

R0 and active case versus time.

Full size image
Figure 5
figure 5

The transmission parameters versus time.

Full size image

  • Period 1 (4th June—15th June 2020)

    The estimated parameters from the model are, α = 0.0934, β = 0.0027, γ = 0.1115, δ = 0.0034, σ = 0.0439, µ =0.0363, ρ = 0.0249, τ = 0.0100, r1 = 0.0745, r2 = 0.0364, r3 = 0.0281, r4 = 0.0227, θ1 = 0.4032, θ2 = 0.9101, θ3 = 0.0352. The corresponding reproduction number is R0 = 1.5802.

  • Period 2 (16th June—27th June 2020)

    The estimated parameters from the model in the given period are: α = 0.0655, β = 3.12e-06, γ = 0.1217, δ = 0.0515, σ = 0.10449, µ = 0.0516, ρ = 0.0267, τ = 0.00999, r1 = 0.04296, r2 = 0.0809, r3 = 0.02769, r4 = 0.0155,1 = 0.313, θ2 = 0.855, θ3 = 0.0126. The corresponding reproduction number is R0 = 1.4811.

  • Period 3(28th June—10th July 2020)

    The estimated parameters are from the model are: α = 0.0770, β = 0.00858, γ = 0.11738, δ = 0.00866, σ = 0.0805, µ = 0.0276, ρ = 0.0260, τ = 0.00304, r1 = 0.04538, r2 = 0.0689, r3 = 0.02557, r4 = 02.53e-05, θ1 = 0.2984, θ2 = 0.739, θ3 = 0. 000341. The corresponding reproduction number is Rv = 1.3071.

  • Period 4 (11th July—20th July 2020)

    During the period, the resulting parameter value estimates are: α = 0.0818, β = 0.000969, γ = 0.1121, δ = 0.00112, σ = 0.00952, µ = 0.0109, ρ = 0.02679, τ = 0.00999, r1 =0.0591, r2 = 0.05591, r3 = 0.02823, r4 = 0.00089, θ1 = 0.2278, θ2 = 0.7479, θ3 = 9.59e-05. The corresponding R0 is 1.4392.

  • Period 5 (21st July—30th July 2020)

    At the end of this period, the estimates are α = 0.07597, β = 0.000893, γ = 0.10960, δ = 0.00205, σ = 0.03988, µ = 0.01678, ρ = 0.02577, τ = 0.00999, r1 =0.0455, r2 = 0.09789, r3 = 0.02673, r4 = 2.571e-08, θ1 = 0.2661, θ2 = 0.7753, θ3 = 0.01952.The corresponding R0 is 0.9761.

Prediction of pandemic size

The data from June 4th to July 30th (57 days) is fitted using 9 differential equations as given in (1.18) and the corresponding parameters are estimated. Figure 6a depicts the projection of infected case, recovered case and deaths, and Fig. 6b depicts that of mild, moderate and altogether.

Figure 6
figure 6

(a) The pandemic size of different clinical stage versus time—infected case, the recovered case and death case. (b) The pandemic size of different clinical stage versus time—mild, moderate and all the cases together.

Full size image

Based on the parameters obtained during Period 5 (21st July–30th July 2020), with the assumption that the policy remains the same, we predicted the susceptible, infected and recovered cases and these are presented in Fig. 7. It is observed that even after 150 days from June 4, 95% of the total population will remain susceptible (i.e.,not get infected) and 0.4% are infected provided we can keep basic reproduction number \({R}_{0}\) less than 1 by ensuring social distancing.

Figure 7
figure 7

The prediction of susceptible, recovered cases and cases of deaths.

Full size image

Sensitivity analysis of the model with respect to varying parameters

We analyzed the sensitivity of the model on infected and, recovered cases and cases of death cases concerning transmission parameters, which would help the policymakers to plan appropriate strategies to mitigate the spread of the disease.

Figure 8 depicts ‘how infected case changes with respect to transmitting parameters. Figure 8a-d illustrates how the nature of pandemic changes along with R0 based on the transmitting parameters, α, β, γ, δ. The parameters are scaled using scaling factors 0.5, 0.8, 1.4, 1.8 and 2,2 on their current value during period 5.

Figure 8
figure 8figure 8

(a-d) The infected and R0 versus scale factor of α, β, γ and δ.

Full size image

Figure 9 shows the sensitivity of transmission parameters with respect to the recovered cases.

Figure 9
figure 9

The sensitivity of transmission parameters over recovered case.

Full size image

Figure 10 shows the sensitivity of transmission parameters with respect to the death cases.

Figure 10
figure 10

The sensitivity of transmission parameters over death cases.

Full size image

Discussion

Based on the public data38,39, the situation in Oman at the end of May was not very severe. Muscat governorate reported more cases compared to other governorates. From the beginning itself, the Oman government has imposed strict measurements to control the disease. Oman Supreme committee has taken a good decision to close the main containment zone, Muscat governorate by April 10 which resulted in the reduction of the transmission rate. By April 29, 2020, the government lifted the restriction on travel inside the governorate except in and out of the Muscat governorate. More number of random tests were conducted in the main containment zones of Muscat governorate such as Muttrah, Seeb, Muscat Province and Al Amerat. It was made compulsory to wear masks in public places and thermal imaging was also done while entering majority of shops in Muscat. The entry to shops was restricted to people with a temperature of more than 37.5 °C, and children of age less than 12 years of old were also not permitted. These decisions were a part of several measures broadcasted by the Municipality as per decision number 199/2020, which lists out 15 safety measures to be practiced by the commercial establishments. Fines were also imposed on those who violates the rule. Lockdown in Muscat province, including the capital Muscat, was lifted entirely on Friday, May 29, as the government began easing the containment measures in place, nationwide. Additionally, at the end of May 2020, the government announced that at least 50 percent of public sector employees could resume working from their offices from Sunday, May 31.

In this research, the significant 15 parameters mentioned in the proposed model is calculated during the said period (Period 1–Period 5) mentioned in Sect. 3, where significant change is observed in the data. The corresponding basic reproduction number R0 is calculated and this depicts the nature of the pandemic with respect to the the spread of the disease.

During Period 1, a partial lifting of the restrictions was observed after a 2-month lockdown period. The value of R0 is found to be 1.5802. During Period 2, the ministry ensured strict social measures to stop the spreading of the disease. Timely instruction is given through official social media account39, such as the importance of washing hands, social distancing etc. At the same time, authorities took necessary care to convey the people not to be panic so that they can reduce the overstress in this situation. Otherwise, ultimately it will affect the living conditions and the business and working environments. More tests were conducted to avoid panic in people. As a result, a slight change resulted in social parameters like \(\alpha\), \(\beta\) and the new reproduction number becomes R0 = 1.4811.

During Period 3, isolation and quarantine policies were made stricter during the period from 28th June-10th July 2020. Anyone who enters the Sultanate was subjected to quarantine for 14 days. The Omani residents were not permitted to go outside the Sultanate. The land and air borders were closed. Because of this strict isolation and quarantine process, and basic social distancing measures among people (such as washing hands often, not touching one’s face, avoiding handshakes etc.) the value of R0 became 1.3071. During the period 11th July–20th July 2020, due to the lack of strict lockdown and an increase in the number of random tests in the containment zones, more infected cases were reported. The Supreme Committee in Oman advised the public to wear face masks in public places, and for business establishments to ensure that the visitors also followed the required safety measures. The spread of the disease was little more during this period, which resulted in R0 value of 1.4392.

From 21st July–30th July, a nationwide lockdown came into effect. Travel between the governorates was not allowed. The emergency services such as ambulances, service vehicles that provide electricity and water maintenance, and vehicles belonging to the police and Armed Forces, were exempted from this ban. People remained indoors between 7 P.M. and 6 A.M. It was not permitted at all to go outside after 7 P.M., either on foot or in a vehicle. Such incidents were imposed with proper fines. Royal Oman Police set several checkpoints on the roads that connect diverse areas of the Sultanate, to ensure domestic travel restrictions. Working was no longer a valid reason for going out of the house; progressively non-indispensable activities were also stopped. As a result, at the end of July, R0 value became 0.9761. It shows that the restriction of the contact with each other in various form significantly brings down the value of R0, thereby decreasing the spread of the disease.

Based on the parameters obtained during period 5 (21st July–30th July 2020) and with the assumption that the policy will remain the same, we predicted the infected size, recovery size and death cases up to 150 days. It is expected to have the number of cumulative infected cases as 236,436, the number of recovery cases as 207,839 and no of deaths as 9234 at the end of 150 days starting from June 04, 2020, provided no change in the policy decisions as on during period 5.

The sensitivity of the model is also analyzed on infected, recovered and death cases concerning transmission parameters as given in “Results” section. The sensitivity analysis on infected case shows that the transmission parameters alpha and gamma are very much sensitive to the spread of the disease. The reason for the high sensitivity of gamma is due to the fact that Moderate category people (M) have a higher probability rate of transmitting the disease as they are in the infectious stage and they are only isolated to their homes and, not admitted in the hospital. The people in the exposed (E) category have a higher rate of a chance of contact with other people as at this stage disease is not diagnosed, and it is infectious to a certain extent which results in higher sensitivity of alpha parameter. The lockdown and social distancing measures such as wearing a mask, avoiding gathering, closing schools and mosques etc. will help significantly reducing the value of these parameters.

The sensitivity analysis on recovered case shows that as the value of transmission parameters increases the number of recovered cases also increases. This is because the infected cases increase with the rise in parameters, and accordingly the number of recovered cases also rise due to the dedicated service of our health centers. In sensitivity analysis of death cases, as parameter value increases, the number of death case may also increase. But due to our medical service, the rise in the value may not be alarming. So, in addition to fineness in our medical field, it is a vital role to frame an appropriate policy to reduce the value of the parameter to control the disease like COVID-19 due to the absence of a specific vaccine for the disease.

It is observed that the transmission parameters are very much influenced by various remedial measures such as lockdown, social distancing and quarantine. This would reduce/increase the basic reproduction number which is the probability of disease transmission in a single contact multiplied by the average number of contacts per person. Since the transmission rate α is due to the contacts between susceptible and exposed (Et), its rate can be reduced through contact tracing and isolate them from the contact of others. The mass random test will also help to identify this category of exposed population (Et) who transmits the disease without showing any symptoms.

Conclusion and future

In this work, we have developed a mathematical model to analyze the nature of the pandemic COVID-19 meaningfully on the data of the Sultanate of Oman. The model is an extension of SEIR where we expanded the infected compartments into mild (A), moderate (M), severe (H) and critical (C), based on the clinical stages of infection. The exposed category is also extended to EN and ET where ET is an infectious stage. The parameters are estimated by fitting the data of Oman on the differential equations, and R0 is computed. The proof for the computation of R0, steady-state analysis and final pandemic size equations are also shown to validate the model. The parameter value is justified with the effective actions taken by the government to lessen the spread of the disease. The sensitivity of the transmitting parameters is also identified which is a direct indicator of the impact of the strict or weak lockdown measures on the spread of the disease. It is observed that the transmitting parameters alpha and gamma are sensitive to the number of infected cases, and their value can be reduced by proper contact tracing mechanism and effective social distancing measures. In conclusion in Oman, there is no need for any complete lockdown as per the present situation. This research can be extended by analyzing the data of Oman by taking Wilayat wise or governorate wise data in Oman. This can also be done for any country by considering the different factors such as population, culture, age distribution, regulations etc. Also, the model can be extended by incorporating the impact of suitable vaccination once it is discovered.