Modeling for COVID-19 with the contacting distance

Abstract

COVID-19 is a public health emergency for human beings and brings some very harmful consequences in social and economic fields. In order to model COVID-19 and develop the effective control measures, this paper proposes an SEIR-type epidemic model with the contacting distance between the healthy individuals and the asymptomatic or symptomatic infected individuals, and the immigration rate of the healthy individuals since the contacting distance and the immigration rate are two critical factors which determine the transmission of COVID-19. Firstly, the threshold values of the contacting distance and the immigration rate are obtained to analyze the presented model. Secondly, based on the data from January 10, 2020, to March 18, 2020, for Wuhan city, all parameters are estimated. Finally, based on the estimated parameters, the sensitivity analysis and the numerical study are conducted. The results show that the contacting distance and the immigration rate play an important role in controlling COVID-19. Meanwhile, the extinct lag decreases as the contacting distance increases and/or the immigration rate decreases. Our study could give some reasonable suggestions for the health officials and the public and provide a theoretical issue for globally controlling the COVID-19 pandemic.

1 Background

Coronaviruses are the enveloped, single-stranded, positive-sense RNA viruses and belong to the family of Coronaviridae [1, 2]. They could induce wildly respiratory infections, even though are accompanied by the relatively low mortality. Since their discovery and first characterization by the UK in 1965 [3], two large-scale outbreaks have occurred and induced the public health events. For examples, the Severe Acute Respiratory Syndrome (SARS) in 2003 in mainland China [4], and the Middle East Respiratory Syndrome (MERS) in 2012 in Saudi Arabia [5,6,7]. These outbreaks have resulted in more than 8000 and 2200 confirmed SARS and MERS cases, respectively [1, 8].

At the end of 2019, a third bigger outbreak occurred in the whole world. On December 29th 2019, four cases were reported by the Wuhan Municipal Health Commission (WMHC) and all confirmed cases are seemingly linked to the Huanan (Southern China) Seafood Wholesale Market (HSWM) [9,10,11,12]. These reported cases were firstly identified as the novel coronavirus-infected pneumonia, and then the World Health Organization (WHO) named this infectious disease as the coronavirus disease 2019, being simplified as COVID-19, on February 11th, 2020 [10, 13]. On January 20th, 2020, the Chinese government revised the law provisions about COVID-19 and defined it as class B agent. Public health officials announced a further revision to classify it as class A agent. Some non-pharmaceutical interventions, including the intensive contact tracing followed by quarantine of individuals potentially exposed to the infected peoples, the isolation of the symptomatic infected individuals and so all, were subsequently adopted, and then gave some positive effect on control of COVID-19.

COVID-19 has already caused a huge economic loss due to national lockdowns, travel restrictions, and global distractions of trade and manufacturing chains, and a large number of deaths due to the shortage of medical resources. Therefore, COVID-19 is a seriously public health emergency for the whole world and brings some very harmful consequences in social and economic fields [8,9,10,11,12, 14]. In order to prevent and control COVID-19 effectively, lots of researchers have conducted to study COVID-19 based on medicine, epidemiology, biology and mathematics [2, 9,10,11,12]. Li et al. [10] collected the confirmed information on demographic characteristics, exposure history and illness timelines of laboratory-confirmed cases that had been reported on January 22th, 2020. They described characteristics of the cases and estimated the key epidemiologic time-delay distributions (the 95th percentile of the distribution at 12.5 days), the epidemic doubling time (DT = 7.4 days) and the basic reproductive number ($R_0=2.2$ (95$\%$ CI, 1.4–3.9)). Fortunately, in the early period, this research has successfully characterized and predicted some critical properties of COVID-19. However, as the development of COVID-19 and the adoptions of some effective prevention and control measures, COVID-19 should be re-estimated. Tang et al. [2] presented a general SEIR-type epidemiological model and estimated the basic reproduction number by means of mathematical modeling. Their results showed that the control reproduction number might be as high as 6.47 (95$\%$ CI, 5.71–7.23). As recognized by the World Health Organization (WHO), the mathematical models, which are employed to describe COVID-19, play an important role for the disease prevention and control, and the policy formation.

The published researches have shown that the main transmission route of the COVID-19, including all epidemic diseases induced by the coronaviruses, is the respiratory transmission [2,3,4, 15, 16]. Hence, keeping the essential contacting distance between the healthy groups and the infected groups is very important for controlling COVID-19. Contacting distance refers to the extent to which people experience a sense of familiarity (nearness and intimacy) or unfamiliarity (fairness and difference) between themselves and people belonging to different social, ethnic, occupational and religious groups from their own [17,18,19,20,21]. The contacting distance describes the distance between different groups, and this notion includes all differences such as social class, race/ethnicity or sexuality, but also the fact that the different groups do not mix [17, 18]. Therefore, in the mathematically modeling processes, the contacting distance between the healthy groups and the symptomatic infected ones is a critical parameter which determines the control measures for COVID-19. Motivated by these, this paper will present an SEIR-type model incorporating the contacting distance between the healthy groups and the infected groups and mainly focus on exploiting the control measures for the COVID-19 based on the contacting distance. This paper will determine the threshold contacting distance between the healthy groups and the infected groups, and COVID-19 will be ultimately controlled when the contacting distance between the healthy groups and the infected groups is larger than this threshold contacting distance. Otherwise, COVID-19 may not be extinct. Here, the threshold contacting distance is a critical value, and COVID-19 will be extinct under this threshold contacting distance and COVID-19 may be endemic above this threshold contacting distance.

2 Method

In this section, an epidemic SEIR-type model with the contacting distance between the healthy groups and the symptomatic infected groups are presented to describe the spread of COVID-19 based on the following two steps.

Step 1.:

Proposing an SEIR-type epidemic model for COVID-19 with the incidence rate which will be presented in the later step 2.

($A_{11}$):

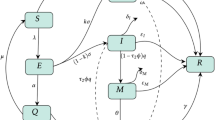
Based on the spreading mechanism of COVID-19, the total populations are divided into five subclasses: the susceptible subpopulation (S(t)), the incubation subpopulation (E(t)), the asymptomatic infected subpopulation ($I_A(t)$), the symptomatic infected subpopulation (I(t)) and the recovered subpopulation (R(t)).

($A_{12}$):

The mean migrating rate of susceptible population for a local region, which describes the local outdoor movements of the susceptible individuals during the spread of COVID-19, is a constant recruitment A, which is defined in the interval $[0, +\infty )$. If the mean migrating rate is larger than zero and smaller than one, it means that individuals can only immigrate into the objective streets from their own home in their own local region. If the mean migrating rate is larger than one, it implies that some parts of individuals immigrate to the objective streets of the local region from the other regions.

($A_{13}$):

The natural death rates of all subpopulation are proportional to their existing densities, and the proportional coefficient is $\mu$. The death rates of the asymptomatic infected subpopulation and symptomatic infected subpopulation are proportional to their existing densities, and the proportional coefficients are $\mu _{21}$ and $\mu _{22}$, respectively. The death rates of the incubation subpopulation could be omitted according to the report of the National Health Commission of the People’s Republic of China (NHCPRC) and the World Health Organization (WHO).

($A_{14}$):

The conversion rates from the incubation subpopulation to the asymptomatic infected subpopulation and the symptomatic infected subpopulation are proportional to the former’s density and the proportional coefficients are $\gamma _{11}$ and $\gamma _{12}$, respectively. These conversion rates are mainly determined by the incubation period of COVID-19.

($A_{15}$):

The recovery rate of the asymptomatic infected subpopulation and symptomatic infected subpopulation is proportional to their densities, and the proportional coefficients are $\gamma _{21}$ and $\gamma _{22}$, respectively. These are mainly determined by their autoimmunity and the medical level of the local hospitals. At present, the recovery rate of the symptomatic infected individuals prominently increases under the effective medical measures being adopted by the local government.

($A_{16}$):

The conversion rates from the susceptible subpopulation to the asymptomatic infected subpopulation and the asymptomatic infected subpopulation are defined as the incidence rate which are proposed in the following step 2.

Step 2.:

According to our published work [19] which was done by some authors of this paper, we present the two incidence functions with the contacting distance explicitly for the asymptomatic and symptomatic infected populations induced by COVID-19 as the following form, respectively.

($\mathrm{IF}(I_A)$):

The incidence functions with the contacting distance explicitly for the asymptomatic infected populations

$$\begin{aligned} \begin{array}{l} \mathrm{IF}(I_A)=\dfrac{\beta _1(1-d)S I_A}{1+\beta _1(1-d)h_1I_A}, \end{array} \end{aligned}$$

(2.1)

where $\beta _1$ is the natural infectious rate of the asymptomatic infected individuals who are carrying the coronavirus-2019, $h_1$ is the average effective contacting time of each asymptomatic infected individual carrying the coronavirus-2019.

Again, the term $\beta _1(1-d)I_A$ measures the positive infection force of COVID-19 for each susceptible individual, and the term $\dfrac{1}{1+\beta _1(1-d)h_1 I_A}$ describes the inhibition effect when the number of the asymptomatic infected individuals increases. At present, this inhibition effect for COVID-19 is always existing since peoples are wearing the gauze masks and staying away from the crowds as far as possible under the media effect and fear effect for COVID-19. It is obtained that the term $\lim _{I_A \rightarrow +\infty }\dfrac{N(I_A)}{T}=\dfrac{1}{h_1}$ is constant, in other words, the infectious ability of COVID-19 will be saturated when the number of the asymptomatic infected individuals is large enough since the asymptomatic infected individuals are quarantined.

($\mathrm{IF}(I)$):

The incidence functions with the contacting distance explicitly for the symptomatic infected populations

$$\begin{aligned} \begin{array}{l} \mathrm{IF}(I)=\dfrac{\beta _2(1-d)S I}{1+\beta (1-d)h_2I}, \end{array} \end{aligned}$$

(2.2)

where $\beta _2$ is the intrinsically infectious rate of the symptomatic individuals infected by COVID-19, $h_2$ is the average outdoor time of each symptomatic individuals infected by COVID-19.

Table 1 The epidemiological meanings of parameters in model (2.3)

It is reasonable to assume that $\beta _1<\beta _2$ and $h_1<h_2$.

Based on the above two steps, the epidemic model for COVID-19 incorporating the contacting distance is presented as the following form:

$$\begin{aligned} \begin{array}{l} {\dot{S}}(t)=A-\dfrac{\beta _1(1-d)SI_A}{1+\beta _1(1-d)h_1I_A}\\ \qquad \qquad \qquad -\dfrac{\beta _2(1-d)SI}{1+\beta _2(1-d)h_2I}-\mu S,\\ {\dot{E}}(t)=\dfrac{\beta _1(1-d)SI_A}{1+\beta _1(1-d)h_1I_A}+\dfrac{\beta _2(1-d)SI}{1+\beta _2(1-d)h_2I}\\ \qquad \qquad -\mu E-\mu _1 E-\gamma _{11}E-\gamma _{12}E,\\ \dot{I_A}(t)=\gamma _{11}E-\mu I_A-\mu _{21} I_A-\gamma _{21} I_A,\\ {\dot{I}}(t)=\gamma _{12}E-\mu I-\mu _{22} I-\gamma _{22} I,\\ {\dot{R}}(t)=\mu _1 E+ \gamma _{21} I_A+\gamma _{22} I-\mu R,\\ \nonumber \end{array}\\ \end{aligned}$$

(2.3)

with the initial conditions:

$$\begin{aligned} \begin{array}{l} S(0) \ge 0,~~E(0) \ge 0,~~I_A(0) \ge 0,\\ I(0) \ge 0,~~R(0) \ge 0. \end{array} \end{aligned}$$

(2.4)

The epidemiological meanings of all parameters of model (2.3) are listed in the following Table 1.

Note that the recover variable R(t) does not appear in the first four equations of model (2.3), this paper focuses on the following subsystem which mainly determines the dynamical behaviors of the original model system:

$$\begin{aligned} \begin{array}{l} {\dot{S}}(t)=A-\dfrac{\beta _1(1-d)SI_A}{1+\beta _1(1-d)h_1I_A}\\ \qquad \qquad \qquad -\dfrac{\beta _2(1-d)SI}{1+\beta _2(1-d)h_2I}-\mu S,\\ {\dot{E}}(t)=\dfrac{\beta _1(1-d)SI_A}{1+\beta _1(1-d)h_1I_A}+\dfrac{\beta _2(1-d)SI}{1+\beta _2(1-d)h_2I}\\ \qquad \qquad -\mu E-\mu _1 E-\gamma _{11}E-\gamma _{12}E,\\ \dot{I_A}(t)=\gamma _{11}E-\mu I_A-\mu _{21} I_A-\gamma _{21} I_A,\\ {\dot{I}}(t)=\gamma _{12}E-\mu I-\mu _{22} I-\gamma _{22} I,\\ \nonumber \end{array}\\ \end{aligned}$$

(2.5)

with the initial conditions:

$$\begin{aligned} \begin{array}{l} S(0) \ge 0,~~E(0) \ge 0,~~I_A(0) \ge 0,~~I(0) \ge 0. \end{array} \end{aligned}$$

(2.6)

3 Results

3.1 Basic property

In order to guarantee the ecologically and epidemically realistic meanings of model (2.5) and model (2.6) with their own initial conditions, the positivity and boundness of all solutions of model (2.5) and model (2.6) with their own initial conditions should be validated.

Proposition 3.1.1

All solutions (S(t), E(t), $I_A(t)$, I(t), R(t)) of model (2.5) with the initial conditions (2.6) are positive on the finite region for all $t>0$.

Proposition 3.1.2

All solutions (S(t), E(t), $I_A(t)$, I(t), R(t)) of model (2.5) with the initial conditions (2.6) are bounded on the finite region in the following set $\Omega$, where

$$\begin{aligned} \Omega= & {} \{(S(t), E(t), I_A(t), I(t)), R(t))\in R^5_+~ \mid \\&\quad ~0<S(t)+E(t)+I_A(t)+I(t))+ R(t)\\\le & {} \dfrac{A}{\mu }\}. \end{aligned}$$

Based on the above theorems, the presented model (2.5) with the initial conditions (2.6) is mathematically well-behaviored, and has its own epidemiological and ecological meanings. Hence, the realistic aspects and properties of model (2.5) with the initial conditions (2.6) are also guaranteed. Next, this paper focuses on the dynamical behaviors of model (2.5) with the initial conditions (2.6) and the theoretically controlling methods for the epidemic diseases.

3.2 The basic reproduction number

In order to describe the expected number of secondary cases produced by a typical infective individual while considering the intervention strategies, the reproduction number $R_0$ of model (2.5) is defined by the theory of the next-generation matrix [21]

$$\begin{aligned} R_0=\rho ((DF\mid _{P_0}) \bullet (DV\mid _{P_0})^{-1}), \end{aligned}$$

in which F is the regeneration matrix matrix and V is the transition matrix of model (2.5).

In order to compute the reproduction number $R_0$ of model (2.5), let

$$\begin{aligned} F= \left( \begin{array}{c} \dfrac{\beta _1(1-d)S I_A}{1+\beta _1(1-d)h_1 I_A}+ \dfrac{\beta _2(1-d)S I}{1+\beta _2(1-d)h_2 I}\\ 0 \\ 0\\ 0\\ 0 \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} V= \left( \begin{array}{c} \dfrac{\beta _1(1-d)S I_A}{1+\beta _1(1-d)h_1 I_A}+ \dfrac{\beta _2(1-d)S I}{1+\beta _2(1-d)h_2 I}\\ (\mu +\mu _1+\gamma _{11}+\gamma _{12})E \\ (\mu +\mu _{21}+\gamma _{21}) I_A-\gamma _{11}E\\ \mu R-\mu _1 E+ \gamma _{21} I_A-\gamma _{22} I\\ \dfrac{\beta _1(1-d)SI_A}{1+\beta _1(1-d)h_1I_A}+\dfrac{\beta _2(1-d)SI}{1+\beta _2(1-d)h_2I}+\mu S-A \end{array}\right) . \end{aligned}$$

Hence, it is obtained that

$$\begin{aligned} \mathrm{DF}\mid _{P_0}= \left( \begin{array}{ccccc} 0 &{} \dfrac{\beta _1(1-d)A}{\mu } &{} \dfrac{\beta _2(1-d)A}{\mu } &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} \mathrm{DV}\mid _{P_0}= \left( \begin{array}{ccccc} \mu +\mu _1+\gamma _{11}+\gamma _{12} &{} 0 &{} 0 &{} 0 &{} 0 \\ -\gamma _{11} &{} \mu +\mu _{21}+\gamma _{21} &{} 0 &{} 0 &{} 0\\ -\gamma _{12}&{} 0 &{} \mu +\mu _{22}+\gamma _{22}&{} 0 &{} 0\\ -\mu _1 &{} -\gamma _{21} &{} -\gamma _{22} &{} \mu &{} 0\\ 0 &{} \dfrac{\beta _1(1-d)A}{\mu } &{} \dfrac{\beta _2(1-d)A}{\mu } &{} 0 &{} \mu \end{array}\right) . \end{aligned}$$

Thus, we have

$$\begin{aligned} (\mathrm{DV}\mid _{P_0})^{-1}= \left( \begin{array}{ccccc} \dfrac{1}{\mu +\mu _1+\gamma _{11}+\gamma _{12}} &{} 0 &{} 0 &{} 0 &{} 0 \\ \dfrac{1}{(\mu +\mu _1+\gamma _{11}+\gamma _{12})(\mu +\mu _{21}+\gamma _{21})} &{} \dfrac{1}{\mu +\mu _{21}+\gamma _{21}} &{} 0 &{} 0 &{} 0\\ \dfrac{1}{(\mu +\mu _1+\gamma _{11}+\gamma _{12})(\mu +\mu _{22}+\gamma _{22})} &{} 0 &{} \dfrac{1}{\mu +\mu _{22}+\gamma _{22}}&{} 0 &{} 0\\ a_{41} &{} \dfrac{\gamma _{21}}{\mu (\mu +\mu _{21}+\gamma _{21})} &{} \dfrac{\gamma _{22}}{\mu (\mu +\mu _{22}+\gamma _{22})} &{} \dfrac{1}{\mu } &{} 0\\ a_{51} &{} \dfrac{\beta _1(1-d)A}{\mu (\mu +\mu _{21}+\gamma _{21})} &{} \dfrac{\beta _2(1-d)A}{\mu (\mu +\mu _{22}+\gamma _{22})} &{} 0 &{} \dfrac{1}{\mu } \end{array}\right) , \end{aligned}$$

in which

$$\begin{aligned} {\left\{ \begin{array}{ll} a_{41}=\dfrac{\mu \mu _1 (\mu +\mu _{21}+\gamma _{21})(\mu +\mu _{22}+\gamma _{22})+ \mu \gamma _{11} \gamma _{21} (\mu +\mu _{22}+\gamma _{22}) +\mu \gamma _{12} \gamma _{22} (\mu +\mu _{21}+\gamma _{21})}{|\mathrm{DV}|}>0,\\ a_{51}=-\dfrac{ \beta _1(1-d) A \gamma _{11} (\mu +\mu _{22}+\gamma _{22})+ \beta _2(1-d) A \gamma _{12} (\mu +\mu _{21}+\gamma _{21})}{ |\mathrm{DV}|}<0. \end{array}\right. } \end{aligned}$$

(3.1)

Therefore, the basic reproduction number is

$$\begin{aligned} R_0= & {} \rho ((\mathrm{DF}\mid _{P_0}) \bullet (\mathrm{DV}\mid _{P_0})^{-1})\nonumber \\= & {} \dfrac{(1-d) A}{\mu (\mu +\mu _1+\gamma _{11}+\gamma _{12})}\nonumber \\&\left( \dfrac{ \beta _1 \gamma _{11}}{\mu +\mu _{21}+\gamma _{21}}+\dfrac{ \beta _2 \gamma _{12}}{\mu +\mu _{22}+\gamma _{22}}\right) . \end{aligned}$$

(3.2)

3.3 The extinct threshold value

In this section, the importantly interesting thing is to consider the dynamical behavior of the disease-free equilibrium since the main focus is to develop the controlling methods for COVID-19.

Clearly, the disease-free equilibrium point of model (2.5) $P_0$ is $(\dfrac{A}{\mu },0,0,0)$, and we mainly consider the dynamical behavior of the disease-free equilibrium point $E_0$.

The Jacobia matrix of model (2.5) at the disease-free equilibrium point $P_0$ is as follows

$$\begin{aligned} J_{P_0}= \left( \begin{array}{cccc} -\mu &{}0 &{} - \dfrac{A_4(1-d)}{\gamma _{11}} &{} -\dfrac{A_5(1-d)}{\gamma _{12}} \\ 0 &{} -A_1 &{} \dfrac{A_4(1-d)}{\gamma _{11}} &{} \dfrac{A_5(1-d)}{\gamma _{12}}\\ 0 &{} \gamma _{11} &{} -A_2 &{} 0\\ 0 &{} \gamma _{12} &{} 0 &{} -A_3 \end{array}\right) . \end{aligned}$$

where

$$\begin{aligned} {\left\{ \begin{array}{ll} A_1=\mu +\mu _1+\gamma _{11}+\gamma _{12}>0,\\ A_2=\mu +\mu _{21}+\gamma _{21}>0,\\ A_3=\mu +\mu _{22}+\gamma _{22}>0,\\ A_4=\dfrac{\beta _1 \gamma _{11}A}{\mu }>0,\\ A_5=\dfrac{\beta _2 \gamma _{12}A}{\mu }>0. \end{array}\right. } \end{aligned}$$

(3.3)

Therefore, the characteristic equation of model (2.5) at the disease-free equilibrium point $P_0$ is presented by the following form:

$$\begin{aligned} \begin{array}{l} (\lambda +\mu )(\lambda ^3+B_1\lambda ^2+B_2\lambda +B_3)=0, \end{array} \end{aligned}$$

(3.4)

in which

$$\begin{aligned} {\left\{ \begin{array}{ll} B_1=A_1+A_2+A_3>0,\\ B_2=A_1A_2+A_1A_3+A_2A_3\\ \qquad \qquad -A_4(1-d)-A_5(1-d),\\ B_3=A_1A_2A_3-A_3A_4(1-d)-A_2A_5(1-d). \end{array}\right. } \end{aligned}$$

(3.5)

According to Routh–Hurwitz rule, the disease-free equilibrium point is $P_0(\frac{A}{\mu },0,0,0)$ is locally asymptotically stable if and only if

$$\begin{aligned} {\left\{ \begin{array}{ll} B_1>0,~B_3>0,\\ B_1B_2-B_3>0. \end{array}\right. } \end{aligned}$$

(3.6)

Next, two cases are considered:

$$\begin{aligned} \begin{array}{l} B_3>0 \\ \Leftrightarrow A_1A_2A_3-(A_3A_4+A_2A_5)(1-d)>0\\ \Leftrightarrow \dfrac{1-d}{A_1}(\dfrac{A_4}{A_2}+\dfrac{A_5}{A_3})<1\\ \Leftrightarrow \dfrac{(1-d) A}{\mu (\mu +\mu _1+\gamma _{11}+\gamma _{12})}\\ \left( \dfrac{ \beta _1 \gamma _{11}}{\mu +\mu _{21}+\gamma _{21}}+\dfrac{ \beta _2 \gamma _{12}}{\mu +\mu _{22}+\gamma _{22}}\right)<1\\ \Leftrightarrow R_0<1. \end{array} \end{aligned}$$

(3.7)

Again, we have

$$\begin{aligned} \begin{array}{l} B_1B_2-B_3>0\\ \Leftrightarrow (A_1+A_2+A_3) (A_1A_3+A_2A_3\\ \quad +A_1A_2-A_4(1-d)-A_5(1-d))\\ \quad -(A_1A_2A_3-A_3A_4(1-d)-A_2A_5(1-d))>0\\ \Leftrightarrow A_1^2A_3+2A_1A_2A_3+A_1^2A\\ \quad +A_2^2A_3+A_1A_2^2+A_1A_3^2+A_2A_3^2\\ \quad -[(A_1+A_2)A_4+(A_1+A_3)A_5](1-d)>0\\ \Leftrightarrow (A_1+A_3)(A_1A_3+A_2(A_1+A_2+A_3))\\ \quad -[(A_1+A_2)A_4+(A_1+A_3)A_5](1-d)>0\\ \Leftrightarrow 2A_1A_2A_3+A_1A_3^2+A_2^2A_3+A_2A_3^2+A_1A_2^2\\ \quad -(A_1A_4(1-d)+A_1A_5(1-d))\\ \quad -(A_2A_4(1-d)+A_3A_5(1-d))>0.\nonumber \end{array}\!\!\!\!\!\!\!\!\\ \end{aligned}$$

(3.8)

If $R_0<1$, then we have

$$\begin{aligned} \begin{array}{l} 2A_1A_2A_3+A_1A_3^2+A_2^2A_3+A_2A_3^2+A_1A_2^2\\ \qquad -(A_1A_4(1-d)+A_1A_5(1-d))\\ \qquad -(A_2A_4(1-d)+A_3A_5(1-d))\\ \quad>(A_1+A_2)(A_1+A+3)>0.\nonumber \end{array}\\ \end{aligned}$$

(3.9)

Therefore, the disease-free equilibrium point is $P_0(\frac{A}{\mu },0,0,0)$ is locally asymptotically stable if and only if

$$\begin{aligned} \begin{array}{l} R_0<1 \Leftrightarrow d>1\\ -\dfrac{\mu (\mu +\mu _1+\gamma _{11}+\gamma _{12})(\mu +\mu _{22}+\gamma _{22})(\mu +\mu _{21}+\gamma _{21})}{\beta _1 \gamma _{11}A(\mu +\mu _{22}+\gamma _{22})+\beta _2 \gamma _{12}A(\mu +\mu _{21}+\gamma _{21})}>0.\nonumber \end{array}\!\!\!\!\!\!\!\\ \end{aligned}$$

(3.10)

Based on the above analysis, we obtain the following results.

Proposition 3.3.1

Suppose that $\beta _1 \gamma _{11}A(\mu +\mu _{22}+\gamma _{22})+\beta _2 \gamma _{12}A(\mu +\mu _{21}+\gamma _{21})>\mu (\mu +\mu _1+\gamma _{11}+\gamma _{12})(\mu +\mu _{22}+\gamma _{22})(\mu +\mu _{21}+\gamma _{21})$, we have

• (1) If $R_0>1$ or $d<1-\frac{\mu (\mu +\mu _1+\gamma _{11}+\gamma _{12})(\mu +\mu _{22}+\gamma _{22})(\mu +\mu _{21}+\gamma _{21})}{\beta _1 \gamma _{11}A(\mu +\mu _{22}+\gamma _{22})+\beta _2 \gamma _{12}A(\mu +\mu _{21}+\gamma _{21})}$, then the disease-free equilibrium point $P_0$ is unstable,

• (2) If $R_0<1$ or $d>1-\frac{\mu (\mu +\mu _1+\gamma _{11}+\gamma _{12})(\mu +\mu _{22}+\gamma _{22})(\mu +\mu _{21}+\gamma _{21})}{\beta _1 \gamma _{11}A(\mu +\mu _{22}+\gamma _{22})+\beta _2 \gamma _{12}A(\mu +\mu _{21}+\gamma _{21})}$, then the disease-free equilibrium point $P_0$ is locally asymptotically stable.

Proposition 3.3.1 reveals that COVID-19 can be controlled while the contacting distance between the healthy individuals and the symptomatic infected individuals is larger than the threshold value $d^*=1-\frac{\mu (\mu +\mu _1+\gamma _{11}+\gamma _{12})(\mu +\mu _{22}+\gamma _{22})(\mu +\mu _{21}+\gamma _{21})}{\beta _1 \gamma _{11}A(\mu +\mu _{22}+\gamma _{22})+\beta _2 \gamma _{12}A(\mu +\mu _{21}+\gamma _{21})}$. This threshold value decreases with the decrease in the immigration rate of susceptible population.

3.4 Model (2.5) without the asymptomatic infected population

If the asymptomatic infected population is omitted since it is difficult to be found and the infection probability of the asymptomatic individuals is very small, then the model (2.5) will become the following forms

$$\begin{aligned} {\dot{S}}(t)= & {} A-\dfrac{\beta _2(1-d)SI}{1+\beta _2(1-d)h_2I}-\mu S, \nonumber \\ {\dot{E}}(t)= & {} \dfrac{\beta _2(1-d)SI}{1+\beta _2(1-d)h_2I}-\mu E-\mu _1 E-\gamma _{12}E, \nonumber \\ {\dot{I}}(t)= & {} \gamma _{12}E-\mu I-\mu _{22} I-\gamma _{22} I, \end{aligned}$$

(3.11)

with the initial conditions:

$$\begin{aligned} \begin{array}{l} S(0) \ge 0,~~E(0) \ge 0,~~I(0) \ge 0. \end{array} \end{aligned}$$

(3.12)

According to Propositions 3.1.1 and 3.1.2, all solutions of model (3.11) with the initial conditions (3.12) are positive and bounded.

According to the computation of the basic reproduction number of model (2.5) ${\tilde{R}}_0$, the basic reproduction number of model (3.11) is

$$\begin{aligned} \begin{array}{l} \bar{R_0} =\dfrac{\beta _2 \gamma _{12} A (1-d) }{\mu (\mu +\mu _1+\gamma _{12})(\mu +\mu _{22}+\gamma _{22})}. \end{array} \end{aligned}$$

(3.13)

By simple computation, the disease-free equilibrium point of model (3.11) is ${\tilde{P}}_0 (\dfrac{A}{\mu },0,0)$ and the corresponding endemic equilibrium point is ${\tilde{P}}({\tilde{S}}, {\tilde{E}}, {\tilde{I}})$, where

$$\begin{aligned} {\left\{ \begin{array}{ll} {\tilde{S}}=\dfrac{\beta _2 \gamma _{12}(1-d)+\mu (\mu +\mu _1+\gamma _{12})(\mu +\mu _{22}+\gamma _{22})}{\beta _2 \gamma _{12}(1-d)(\mu h_2+1)},\\ {\tilde{E}}=\dfrac{\beta _2 \gamma _{12}(1-d)-\mu (\mu +\mu _1+\gamma _{12})(\mu +\mu _{22}+\gamma _{22})}{\beta _2 \gamma _{12}(1-d)(\mu h_2+1)(\mu +\mu _1+\gamma _{12})},\\ {\tilde{I}}=\dfrac{\beta _2 \gamma _{12}(1-d)-\mu (\mu +\mu _1+\gamma _{12})(\mu +\mu _{22}+\gamma _{22})}{\beta _2 \gamma _{12}(1-d)(\mu h_2+1)(\mu +\mu _1+\gamma _{12})(\mu +\mu _{22}+\gamma _{22})}.\nonumber \end{array}\right. }\!\!\!\!\!\!\!\\ \end{aligned}$$

(3.14)

Clearly, the endemic equilibrium point ${\tilde{P}}$ is positive if and only if ${\bar{R}}_0>1$.

Next, the stability properties of the disease-free equilibrium point ${\tilde{P}}_0$ and the endemic equilibrium point ${\tilde{P}}$ are considered.

Firstly, the Jacobia matrix of model (3.11) at the disease-free equilibrium point ${\tilde{P}}_0$ is as follows

$$\begin{aligned} J_{{\tilde{P}}_0 }= \left( \begin{array}{ccc} -\mu &{} 0 &{} -\dfrac{\beta _2 A (1-d)}{\mu }\\ 0 &{} -A_1 &{} \dfrac{\beta _2 A (1-d)}{\mu }\\ 0 &{}\gamma _{12}&{} -A_3 \end{array}\right) . \end{aligned}$$

The corresponding characteristic equation of model (3.11) at the disease-free equilibrium point ${\tilde{P}}_0$ is

$$\begin{aligned} \begin{array}{l} (\lambda +\mu )(\lambda ^2+(A_1+A_3)\lambda +A_1A_3-A_5(1-d)), \end{array} \end{aligned}$$

(3.15)

Therefore, according to $Routh--Hurwitz$ rule, the disease-free equilibrium point is ${\tilde{P}}_0$ is locally asymptotically stable if and only if

$$\begin{aligned} \begin{array}{l} A_1A_3-A_5(1-d)>0\\ \Leftrightarrow \dfrac{A_5(1-d)}{A_1A_3}<1\\ \Leftrightarrow {\bar{R}}_0<1\\ \Leftrightarrow d>1-\dfrac{\mu (\mu +\mu _1 +\gamma _{12})(\mu +\mu _{22}+\gamma _{22})}{\beta _2 A \gamma _{12}}>0. \end{array} \end{aligned}$$

(3.16)

Secondly, the Jacobia matrix of model (3.11) at the endemic equilibrium point ${\tilde{P}}$ is as follows

$$\begin{aligned} J_{{\tilde{P}}}= \left( \begin{array}{ccc} -\mu -\dfrac{\beta _2 A (1-d){\tilde{I}}}{1+\beta _2 (1-d)h_2 {\tilde{I}}} &{} 0 &{} \dfrac{\beta _2 (1-d)((\mu +\mu _1 +\gamma _{12})(\mu +\mu _{22}+\gamma _{22})-\gamma _{12}A) }{\mu \gamma _{12}(1+\beta _2 (1-d)h_2 {\tilde{I}})^2}\\ \dfrac{\beta _2 A (1-d){\tilde{I}}}{1+\beta _2 (1-d)h_2 {\tilde{I}}} &{} -(\mu +\mu _1 +\gamma _{12}) &{} \dfrac{\beta _2 (1-d)(\gamma _{12}A-(\mu +\mu _1 +\gamma _{12})(\mu +\mu _{22}+\gamma _{22})) }{\mu \gamma _{12}(1+\beta _2 (1-d)h_2 {\tilde{I}})^2}\\ 0 &{}\gamma _{12}&{} -(\mu +\mu _{22}+\gamma _{22}) \end{array}\right) . \end{aligned}$$

The corresponding characteristic equation of model (3.11) at the endemic equilibrium point ${\tilde{P}}$ is

$$\begin{aligned} \begin{array}{l} \lambda ^3+{\tilde{B}}_1\lambda ^2+{\tilde{B}}_2\lambda +{\tilde{B}}_3, \end{array} \end{aligned}$$

(3.17)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} {\tilde{B}}_1=\dfrac{\beta _2 \gamma _{12}A(1-d)(\mu h_2+1)}{\beta _2 \gamma _{12} h_2 (1-d)+A_1A_2}+A_1+A_2,\\ {\tilde{B}}_2=\dfrac{A_1A_2 h_2(\beta _2 \gamma _{12}A(1-d)-\mu A_1A_2)+\beta _2 \gamma _{12}A(1-d)(\mu h_2+1)(A_1+A_2)}{\beta _2 \gamma _{12} h_2 (1-d)+A_1A_2},\\ {\tilde{B}}_3=\dfrac{A_1A_2 (\mu h_2+1)(\beta _2 \gamma _{12}A(1-d)-\mu A_1A_2)}{\beta _2 \gamma _{12} h_2 (1-d)+A_1A_2}. \end{array}\right. } \end{aligned}$$

(3.18)

According to $Routh--Hurwitz$ rule, the endemic equilibrium point ${\tilde{P}}$ is locally asymptotically stable if and only if

$$\begin{aligned} {\left\{ \begin{array}{ll} {\tilde{B}}_1>0,~{\tilde{B}}_3>0,\\ {\tilde{B}}_1{\tilde{B}}_2-{\tilde{B}}_3>0. \end{array}\right. } \end{aligned}$$

(3.19)

Clearly, the terms ${\tilde{B}}_1>0$ and ${\tilde{B}}_3>0$ hold if ${\tilde{R}}_0>1$ or $d<1-\dfrac{\mu (\mu +\mu _1 +\gamma _{12})(\mu +\mu _{22}+\gamma _{22})}{\beta _2 A \gamma _{12}}$.

Again, we have

$$\begin{aligned} \begin{array}{l} {\tilde{B}}_1{\tilde{B}}_2-{\tilde{B}}_3>0\\ \Leftrightarrow \dfrac{\beta _2 \gamma _{12}A(1-d)(\mu h_2+1)(A_1+A_2)^2}{\beta _2 \gamma _{12}A h_2 (1-d)+A_1A_2}\\ -\dfrac{A_1A_2 h_2(\beta _2 \gamma _{12}A(1-d)-\mu A_1A_2)}{\beta _2 \gamma _{12} A h_2 (1-d)+A_1A_2}>0\\ \Leftrightarrow \dfrac{(\mu h_2+1)(\gamma _{12}A(1-d)(A_1^2+A_2^2+A_1A_2)+\mu A_1^2A_2^2)}{\beta _2 \gamma _{12}A h_2 (1-d)+A_1A_2}>0.\nonumber \end{array}\!\!\!\!\!\!\!\\ \end{aligned}$$

(3.20)

Based on the above analysis, we obtain the following results.

Proposition 3.4.1

Suppose that $\beta _2 A \gamma _{12}>\mu (\mu +\mu _1 +\gamma _{12})(\mu +\mu _{22}+\gamma _{22})$, we have

• (1). If ${\bar{R}}_0>1$ or $d<1-\frac{\mu (\mu +\mu _1 +\gamma _{12})(\mu +\mu _{22}+\gamma _{22})}{\beta _2 A \gamma _{12}}$, then the endemic equilibrium point ${\tilde{P}}$ is locally asymptotically stable,

• (2). If ${\bar{R}}_0<1$ or $d>1-\frac{\mu (\mu +\mu _1 +\gamma _{12})(\mu +\mu _{22}+\gamma _{22})}{\beta _2 A \gamma _{12}}$, then the disease-free equilibrium point ${\tilde{P}}_0$ is locally asymptotically stable.

Proposition 3.4.1 reveals that COVID-19, which incorporates the relatively high infection rate, can be controlled while the contacting distance between the healthy individuals and the symptomatic infected individuals is larger than the threshold value $\bar{d^*}=1-\dfrac{\mu (\mu +\mu _1 +\gamma _{12})(\mu +\mu _{22}+\gamma _{22})}{\beta _2 A \gamma _{12}}$. This threshold value decreases with the decrease in the immigration rate of susceptible population. That is to say, the contacting distance could be shortened in the locations with the low population density. The equivalent results of Proposition 3.4.1, which take the immigration rate of susceptible population as the controlling parameter, can also be proposed as follows.

Proposition 3.4.2

We have the following conclusions

• (1) If $0<A<\dfrac{\mu (\mu +\mu _1+ \gamma _{12})(\mu +\mu _{22}+\gamma _{22})}{\beta _2 \gamma _{12} (1-d)}$, then the disease-free equilibrium point ${\tilde{P}}_0$ is locally asymptotically stable,

• (2). If $\dfrac{\mu (\mu +\mu _1 +\gamma _{12})(\mu +\mu _{22}+\gamma _{22})}{\beta _2 \gamma _{12} (1-d)}<A<1$, then the endemic equilibrium point ${\tilde{P}}$ is locally asymptotically stable.

Proposition 3.4.2 reveals that the COVID-19 can be controlled while the immigration rate of susceptible population is smaller than the threshold value $\bar{A^*}=\dfrac{\mu (\mu +\mu _1+\gamma _{12})(\mu +\mu _{22}+\gamma _{22})}{\beta _2 \gamma _{12} (1-d)}$, and this threshold value increases with the increase in the contacting distance between the healthy individuals and the symptomatic infected individuals. That is to say, only if the contacting distance is large enough, the relatively large immigration of local peoples cannot induce the second outbreak of the COVID-19.

4 A case study

Since from January 20, 2020, all data (including information on new cases, cumulative cases, suspected cases, recovered cases and death cases) were provided by National Health Commission of the People’s Republic of China (NHPRC). As for Wuhan city in which the first case was reported, the corresponding data were restricted by many factors, such as the awareness of the epidemiological characteristics of the new coronavirus, the severe lack of medical resources, the processing and fusion capabilities of reported data and insufficient nucleic acid detection capabilities. However, the Wuhan Municipal Government revised some of the final statistical data April 17, 2020 the daily case data have not been revised.

Noting the specific characteristics of the reported data in Wuhan city, data of daily new cases from January 1, 2020, to March 18, 2020, were reported based on the data confirmed by laboratory calculation and testing in the government’s statutory epidemic information reporting system [2, 10, 12]. The results in Hao et al. [22] showed that the diagnosis rate of COVID-19 in Wuhan during this period was 0.13. In this paper, based on the statistic factors such as the calculation and detection capabilities, and the authenticity of data before January 1, 2020, the data from January 1, 2020 to March 18, 2020, are adopted.

Fig. 1

The change tendency of $\bar{R_0}$ with d and A

Fig. 2

Estimation and surveillance of the new infected cases

By the method of Approximate Bayesian Computation Sequential Monte Carlo (ABC-SMC) to fit model (3.11), all parameters are estimated in Table 1. According to the formula (3.13) and the technically selected parameter values, the threshold value of the contacting distance ${\bar{d}}^*$ is 0.8582 and the threshold value of the influx of the susceptible subpopulation ${\bar{A}}^*$ is 0.4396. The basic reproduction number of COVID-19 decreases with increase in the contacting distance between the susceptible individuals, and the asymptomatic infected individuals increases and decreases in the influx of the susceptible subpopulation. The specific distribution is shown in Fig. 1. Figure 1 shows that the basic reproduction number ${\bar{R}}_0$ is less than one if the contacting distance is larger than its threshold 0.8582 and/or the threshold value of the influx of the susceptible subpopulation is less than its threshold 0.4396. Therefore, COVID-19 will be theoretically controlled if the contacting distance is larger than 0.8582 and/or the influx of the susceptible subpopulation is less than 0.4396.

For Wuhan city, before January 23, 2020, the basic reproduction number is 3.52 which is larger than one, this means that COVID-19 will be endemic disease if any control measures are not implemented. However, after January 23, 2020, the initial government interventions including keeping the contacting distance and prohibiting into/out Wuhan City are adopted, then the basic reproduction number is 0.31 which is less than one. Two periods of COVID-19 in Wuhan city are evidently revealed and the specific distribution is clearly shown in Fig. 2. The initial government intervention period from January 8 to January 22, 2020, is shown in the left in Fig. 2. The lockdown period and the pharmaceutical interventions stage from January 23 to March 18, 2020, is shown in the right in Fig. 2. Therefore, the effective measures, such as decrease in the influx of the susceptible subpopulation and increase in the contacting distance between the susceptible individuals and the asymptomatic infected individuals, are important to control COVID-19.

The following sensitivity analysis and numerical simulation show that these two control measures are the effective measures for preventing the transmission of COVID-19.

Table 2 The estimated values of parameters in model (3.11)

4.1 Sensitivity analysis

In this section, the sensitivity analysis for model (3.11) is conducted based on the reported cases of the COVID-19 in Wuhan city and the estimated parameters in Table 1.

In order to identify the key factors which affect the change of the infectious cases, this paper applies Latin Hypercube Sampling (LHS) for parameter sampling and Paranoid Rank Correlation Coefficient (PRCC) method for sensitivity analysis of the parameters in model (3.11). When performing parameter sampling, we choose uniform distribution as the prior distribution, sampling times $N=1000$, the reference values of the parameters of model (3.11) are given in Table 1, and the value range is $20\%$ up and down the reference value. The parameters with p value greater than 0.01 are considered to have no effect on the model.

Fig. 3

PRCC values of parameters in E(t) and I(t) at $t=4000$

Fig. 4

Scatter plot of PRCC value for each parameter in E(t)

Fig. 5

Scatter plot of PRCC value for each parameter in I(t)

Figure 3a and Table 4 show that the parameters A and E(t) are positively correlated, that is, the population of E(t) subgroups will increase as parameter A increases. The parameters $\mu$, $\mu _1$, $\mu _{22}$, $\gamma _{12}$, $\gamma _{22}$ and d are negatively correlated with E(t), that is, increasing $\mu$, $\mu _1$, $\mu _{22}$, $\gamma _{12}$, $\gamma _{22}$ and d will cause E(t) to decrease. Figure 3 shows that the monotonicity of the parameters A, $\mu$, $\mu _1$, $\gamma _{22}$ and d is the most significant and E(t) is mainly affected by these important parameters. Figure 3b and Table 4 show that that the parameters A and $\gamma _{12}$ are positively correlated with I(t), that is, I(t) will increase as A and $\gamma _{12}$ increase. The parameters $\mu$, $\mu _1$, $\mu _{22}$, $\gamma _{22}$, d and I(t) are negatively correlated, that is, the population of I(t) will decrease as the parameters $\mu$, $\mu _1$, $\mu _{22}$, $\gamma _{22}$ and d increase. Furthermore, Fig. 4 reveals that the monotonicity of the parameters A, $\mu$, $\mu _1$, $\mu _{22}$, $\gamma _{12}$, $\gamma _{22}$ and d is the most significant and I(t) is mainly affected by these parameters.

Figure 5 reveals that the PRCC value of each parameter changes significantly in the early stage of the outbreak. Meanwhile, Fig. 5b shows that the parameters A, $\mu$, $\mu _1$, $\gamma _{12}$, $\gamma _{22}$ and d have undergone significant changes being related to I(t). The PRCC values of the parameters A and d show a trend of first increasing, then decreasing and finally increasing again. This is induced by the rapid increase in the number of patients after the outbreak, and the susceptible subpopulation S(t) is more likely to be infected under the small contacting distance with the initial outbreak. At this time, the contacting distance will have a greater impact on the number of patients. With the improvement of people’s awareness of the prevention of epidemics and medical conditions, people’s behavior of reducing the outdoor time and using masks will lead to less and less impact of d on I(t). According to the phased results of the epidemic prevention work, people’s awareness of epidemic prevention will become weaker than before. At this time, the influence of the parameters A and d on I(t) will increase.

Table 3 PRCC value and P value of each parameter in E(t)

Table 4 PRCC value and P value of each parameter in I(t)

Table 5 PRCC value and P value of each parameter in $R_0$

Fig. 6

PRCC values of each parameter in $R_0$

Fig. 7

PRCC value of each parameter over time

Figure 6 and Table 5 show the influence of each parameter on the basic reproduction number $R_0$. The parameters A, $\beta _2$ and $R_0$ are positively correlated, and the parameter A has a greater impact on $R_0$. $R_0$ will increase rapidly as the parameter A increases, and more susceptible people will be infected. The parameters $\mu$, $\mu _1$, $\gamma _{22}$ and d are negatively correlated with $R_0$. Most importantly, $R_0$ will decrease rapidly as the parameter d increases, and the maximum value of PRCCs is $|PRCC(d)| = 0.6973$ which indicates that d has the greatest impact on $R_0$. In other words, as long as d is controlled within a certain range, $R_0$ can be clearly minimized. The changing tendency of the PRCC value of each parameter over time is shown in Fig. 7. Figure 7 reveals that the sensitivity is convergent, and thus the robustness and stability of the sensitivity analysis are guaranteed.

Fig. 8

The disease-free equilibrium point is asymptotically stable with $d=0.91$

Fig. 9

The COVID-19 will be vanished while the contacting distances is larger than the threshold value 0.8582

4.2 Numerical simulation

Figures 8, 9 and 10 show that COVID-19 will be ultimately controlled when the contacting distance is larger than the threshold value 0.8582. Figure 8 selects the contacting distance between the susceptible individuals and the symptomatic infected individuals as 0.91 which is larger than the threshold value 0.8582, and hence COVID-19 will be vanished. Since the parameter d is normalized in the modeling processes, the COVID-19 will be completely controlled only if the susceptible individuals and the symptomatic infected individuals keep their contacting distance to be larger than $0.8582 \times D$, where D is the spreading distance of the coronavirus of COVID-19 when people are breathing and/or sneezing under certain environment. The World Health Organization (WHO) claimed that the spreading distance of the coronavirus of COVID-19 is more than 2 meters and even 4.5 meters under some certain environmental conditions. Hence, individuals should be required to keep away at least 1.7 meters rather than 1.5 meters which is adopted by many disease control departments of some countries. Figure 9 reveals that COVID-19 will be vanished as long as the contacting distance is larger than the threshold value 0.8582, and the extinct lag of COVID-19 closely relates to the contacting distance after January $23^th$, 2020. Furthermore, Fig. 9 shows that the extinct lags decrease of the incubation infected individuals and the symptomatic infected individuals as the contacting distance increase. Figure 9a and b reveals that the minimum extinct lag of the incubation infected individuals is larger than that of the symptomatic infected individuals. Figure 10 reveals that COVID-19 will be vanished when the contacting distance is larger than its threshold value although the immigration rates are less than the threshold value 0.4396, and the extinct lag of COVID-19 has the close relationship with the people’s immigration to Whan city. Furthermore, the extinct lag decreases with the people’s immigrating number to the streets of Wuhan city decreasing. Figure 10a and b shows that the minimum extinct lag of the incubation and the symptomatic infected individuals is smaller than that of the symptomatic infected individuals when the people’s immigrating number to the streets from their own home to Wuhan city is $10\%$ of the resident populations of Wuhan city after January 23, 2020. Moreover, the extinct lag of COVID-19 will become longer when the immigration rate increases. Most interestingly, if the active individuals of the residents of Wuhan city keep the safe contacting distance, their outdoor time of has no influence on the extinction of COVID-19. This implies that some individuals could move outdoors as long as they do not gather and can keep just far enough. Therefore, it is reasonable to suggest that the necessary and safe outdoor activities of the healthy individuals could not induce COVID-19 to be endemic again. Actually, this suggestion is effectively adopted by many countries.

Fig. 10

The COVID-19 will be vanished with $d=0.9$ although the immigration rates are smaller than the threshold value 0.4396

Figures 11, 12 and 13 show that COVID-19 may become endemic disease when the contacting distance is smaller than the threshold value 0.8582. Figure 11 reveals that COVID-19 will become endemic when the contacting distance is smaller than the threshold value 0.8582. Figure 12 reveals that the endemic lag decreases as the contacting distance decreases. Hence, the contacting distance should be increased in order to delay the outbreak of COVID-19. Moreover, Fig. 12a and b shows the minimum endemic lag of the symptomatic infected individuals larger than that of the incubation and symptomatic infected individuals. This means that the symptomatic infected individuals should be exactly and completely treated by the non-pharmaceutical interventions or the pharmaceutical interventions. Figure 13a and b shows that, although the immigrating individuals to the streets from their own home in Wuhan city is smaller than $43.96\%$ of the residents of Wuhan city, COVID-19 may become endemic disease after 28 like-days (two incubation lags) while the contacting distance is 40 percent of the spreading distance of COVID-19.

Fig. 11

The endemic equilibrium point is asymptotically stable with $d=0.5$

Fig. 12

The COVID-19 will be endemic while the contacting distances are smaller than the threshold value 0.8582

Fig. 13

The COVID-19 will be endemic with $d=0.4$ although the immigration rates are smaller than the threshold value 0.4396

5 Discussion and conclusion

In this paper, an SEIR-type epidemic model for COVID-19 incorporating the contacting distance between the susceptible and asymptomatic/symptomatic infected individuals and the influx of the susceptible subpopulation is presented. The contacting distance and the influx of the susceptible subpopulation are explicitly incorporated into the incidence function to consider its influences on the spread of COVID-19. Our results show that the contacting distance and the influx of the susceptible subpopulation play an important role in controlling COVID-19. Furthermore, the corresponding threshold values of the contacting distance and the influx of the susceptible subpopulation, which could induce COVID-19 to be extinct or endemic, are obtained by mathematical analysis based on the ordinary differential equation. Meanwhile, all parameters of the presented model are estimated based on the data of Wuhan city, and the threshold values of the contacting distance and the immigration rate are obtained. The theoretical and numerical conclusions show that COVID-19 will be completely controlled when the contacting distance is larger than the corresponding threshold value ${\bar{d}}^*=1-\frac{\mu (\mu +\mu _1 +\gamma _{12})(\mu +\mu _{22}+\gamma _{22})}{\beta _2 A \gamma _{12}}=0.8582$ and/or the immigration rate is smaller than the corresponding threshold value ${\bar{A}}^*=\frac{\mu (\mu +\mu _1+\gamma _{12})(\mu +\mu _{22}+\gamma _{22})}{\beta _2 (1-d)}=0.4396$. Moreover, the sensitivity analysis reveals that the contacting distance and the influx of the susceptible subpopulation are most sensitive to the transmission of COVID-19.

Our study gives some non-pharmaceutical interventions to control COVID-19 and some reasonable suggestions for the policy-makers. However, our paper uses the average contacting distance in the modeling processes and does not consider the temporal and spatial effects in the contacting distance. Maybe the variable contacting distance with the temporal and spatial factors is more realistic and useful. Meanwhile, our model considers the respiratory transmission and the contacting transmission in the modeling processes only and does not take into account the aerosol transmission. These will be open issues and should be generally considered in the future work.

Appendix

Proof of Proposition 3.1.1

According to differential and integral theory, we have

$$\begin{aligned}&\dfrac{\mathrm{d}}{\mathrm{d}t}\left[ S(t)\exp \left\{ \int ^t_0\dfrac{\beta (1-d(\tau ))E(\tau )}{1+\beta (1-d(\tau ))hE(\tau )}\mathrm{d}\tau +\mu t \right\} \right] \\&\quad =A\exp \left\{ \int ^t_0\dfrac{\beta (1-d(\tau ))E(\tau )}{1+\beta (1-d(\tau ))h E(\tau )}\mathrm{d}\tau +\mu t \right\} . \end{aligned}$$

That is,

$$\begin{aligned}&S(t)\exp \left\{ \int ^t_0\dfrac{\beta (1-d(\tau ))E(\tau )}{1+\beta (1-d(\tau ))h E(\tau )}\mathrm{d}\tau +\mu t \right\} -S(0)\\&\quad =\int ^t_0\left[ A\exp \left\{ \int ^t_0\dfrac{\beta (1-d(\tau ))E(\tau )}{1+\beta (1-d(\tau ))h E(\tau )}\mathrm{d}\tau +\mu t \right\} \right] \mathrm{d}t. \end{aligned}$$

Hence,

$$\begin{aligned} S(t)= & {} \Bigg \{S(0)+\int ^t_0\Bigg [A\exp \Bigg \{\int ^t_0\dfrac{\beta (1-d(\tau ))E(\tau )}{1+\beta (1-d(\tau ))h E(\tau )}\mathrm{d}\tau \\&+\mu t \Bigg \} \Bigg ]\mathrm{d}t \Bigg \}\\&\times \exp \Bigg \{-\int ^t_0\dfrac{\beta (1-d(\tau ))E(\tau )}{1+\beta (1-d(\tau ))h E(\tau )}\mathrm{d}\tau +\mu t \Bigg \}>0. \end{aligned}$$

Similarly, the positivity of the other solutions E(t), $I_A(t)$, I(t) and R(t) can be shown.

Thus, the solution (S(t), E(t), $I_A(t)$, I(t), R(t)) of model (2.5) with the initial conditions (2.6) are positive on the finite region for all $t>0$.

Therefore, the positivity of all solutions of model (2.7) with the initial conditions (2.8) is also guaranteed since model (2.7) is a special case of model (2.5).

Proof of Proposition 3.1.2

Define $N(t)=S(t)+E(t)+I_A(t)+I(t)+ R(t)$ and add all equations of model (2.5), it is obtained that

$$\begin{aligned} \dfrac{\mathrm{d}N}{\mathrm{d}t}=A-\mu N-\mu _1E--\mu _{21}I_A -\mu _{22}I \le A-\mu N. \end{aligned}$$

By comparison theorem, it follows that

$$\begin{aligned} 0 \le N(t) \le \dfrac{A}{\mu }+N(0)e^{-dt}. \end{aligned}$$

Thus,

$$\begin{aligned} \limsup _{t\rightarrow +\infty }N(t) \le \dfrac{A}{\mu }. \end{aligned}$$

Hence, all solutions (S(t), E(t), $I_A(t)$, I(t), R(t)) of model (2.3) with the initial conditions (2.4) are bounded on the finite region and the set $\Omega$ is a positively invariant set for model (2.3) with the initial conditions (2.4).

Therefore, the boundness of all solutions of model (2.5) with the initial conditions (2.6) is also guaranteed since model (2.5) is a special case of model (2.3). $\square$

Proof of Proposition 3.3.1

We will prove the globally asymptotical stability of the disease-free equilibrium point $E_0$. Define the following matrices:

$$\begin{aligned}&\!\!\!W= \left( \begin{array}{lll} S\\ E\\ I \end{array}\right) ,\\&\!\!\!J_{E_0}= \left( \begin{array}{ccc} -\mu &{} 0 &{} -\dfrac{\beta _2 A (1-d)}{\mu }\\ 0 &{} -(\mu +\mu _1+\gamma _{12}) &{} \dfrac{\beta _2 A (1-d)}{\mu }\\ 0 &{}\gamma _{12}&{} -(\mu +\mu _{22}+\gamma _{22}) \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} J^1_{E_0}= \left( \begin{array}{ccc} A-\dfrac{\beta _2 (1-d)SI}{1+\beta _2 (1-d)h_2 I}+\dfrac{\beta _2 A (1-d)E}{\mu }\\ \dfrac{\beta _2 (1-d)SI}{1+\beta (1-d)h_2 }-\dfrac{\beta _2 A (1-d)E}{\mu }\\ 0 \end{array}\right) . \end{aligned}$$

Based on the above definitions and notations, model (2.5) nearing the disease-free equilibrium point $E_0$ can be rewritten as:

$$\begin{aligned} \begin{array}{l} \dfrac{\mathrm{d} W}{\mathrm{d}t}=J_{E_0}W+J^1_{E_0}. \end{array} \end{aligned}$$

(5.1)

By simple computation, the vector $J^1_{E_0}$ is non-positive in the set $\Omega =\{(S,I)|S>0,~I\ge 0 \}$.

Hence, combining Eq. (5.1) with the non-positivity of the vector $J^1_{E_0}$ in the set $\Omega =\{(S,I)|S>0,~I\ge 0 \}$ , we have

$$\begin{aligned} \begin{array}{l} \dfrac{\mathrm{d} W}{\mathrm{d}t}\le J_{E_0}W. \end{array} \end{aligned}$$

(5.2)

According to the local stability of the disease-free equilibrium point, $E_0$ and all characteristic roots of matrix $J_{E_0}$ have negative real parts.

Therefore, the disease-free equilibrium point $E_0$ is globally stable by the theory of the ordinary differential equation.