1 INTRODUCTION

Mathematical models of infection spreading are of particular importance in the case of global pandemics. Even though unable to reproduce entire picture of the pandemic, they provide qualitative predictions of its development and reveal the specific dynamic patterns, which may be helpful in optimal planning of social preventive measures that would allow a certain degree of controlling the situation. These measures are the subject of heated debate, as they significantly change the daily life of people and have large economic consequences. Note, for example, that the effectiveness of social distancing to reduce the peak incidence was demonstrated as long ago as during the Spanish flu pandemic in 1918–1919 [1]. Novel forecasting tools based on mathematical modelling provide an arguable advantage to facilitate the adapting and adjusting process, by promoting efficient resource management at individual and institutional levels.

The attempts of mathematical modeling of infections have a long history of more than a hundred years [2–4]. Later Kermack and McKendrick [5] considered the progress of an epidemic in a closed homogeneous population assuming that complete immunity is conferred by a single attack, and that an individual is not infective at the moment at which he receives infection. With these assumptions, the problem was finally reduced to a Volterra-type integro-differential equation the analysis of which allowed such conclusions as the existence of threshold population density below which no epidemic can occur, the crucial role of small changes of the infectivity rate, and the end of an epidemic before the susceptible population has been exhausted. The model was generalized [6] by considering the effect of the continuous introduction of fresh susceptible individuals into the population (birth, immigration, etc.). Similar results were indicated when the transmission of infection was through an intermediate host [5].

Naturally, the COVID-19 pandemic stimulated a burst of interest to developing prediction tools based on mathematical modelling. Particular aims and approaches of different research teams are rather different. For example, Uhlig et al. [7], based on deterministic compartment models proposed an empirical top-down modeling approach to provide epidemic forecasts and risk calculations for (local) outbreaks. Based on initial results, the authors of [7] foresee a statistical framework of the proposed type to drive web-based automatic platforms to democratize the dissemination of prognosis results.

For operative estimations, simpler models are desirable. The easiest approach is curve fitting of available data. In [8] the number of cumulative diagnosed positive COVID-19 cases \(P(t)\) was assumed to be an error function. This is true if the number of daily new cases \(P'(t)\) can be described by a Gaussian distribution, which is typically not the case [9]. Köhler-Rieper et al. [9] proposed a deterministic forecast model for COVID-19 epidemic in which the model dynamics is expressed by a single prognostic variable \(\kappa (t)\), entering an integro-differential equation as a time-dependent coefficient. The model [9] shows similarities to classic compartmental models, such as SIR [10], and the variable \(\kappa (t)\) can be interpreted as the effective reproduction number. The authors of [9] consider it a principal advantage, since the model is formulated with the most trustable statistical data variable: the number of cumulative diagnosed positive cases of COVID-19. They have applied the model to more than 15 countries and results are available via a web-based platform [11].

As an alternative to integro-differential equation, in the present paper we use an approach based on retarded differential equations [12], a particular case of functional differential equations. Such delay models follow the strategy of modelling the removal process not with a separate variable but with a time shift in the function describing the number of cumulative cases. Dell’Anna [13] presented an example of application of a delay model to COVID-19 problem. The equivalence of integro-differential and retarded differential equations can be demonstrated, e.g., the authors of [9] show that the basic equation of their model is identical to the retarded differential equation in [7] provided the appropriate choice of the integration weighting function.

Our model equation is analogous to the general model of [5, 13], however, the subsequent analysis in [13] is carried out with a simplified equation neglecting the so-called logistic factor (see below), i.e. in a particular case of negligibly small number of infected individuals compared to the population, which is valid globally, but questionable in small populations The interrelation between our model and the SIR model will be analyzed below

2 BASIC DEFINITIONS

\({{N}_{{\max}}}\) is the population size.

\(N(t)\) is the number of infected individuals at the moment of time \(t\).

\(\tau \) is the time, during which the infection can be spread by a single virus carrier. It can be either the natural disease duration, or the time interval from the moment of contamination to the moment of the carrier isolation from communicating with other individuals. In the present consideration, \(\tau \) is a model parameter.

\(N(t - \tau )\) is the number of subjects still ill, but already not virus carriers. Obviously, at \(t - \tau < 0\) it is zero, \(N(t - \tau ) = 0\).

\(N(t) - N(t - \tau )\) is the number of virus carriers at the moment of time \(t\).

\({{N}_{{\max}}} - N(t)\) is the non-infected population size.

\((N(t) - N(t - \tau )){\text{/}}{{N}_{{\max}}}\) is the density of virus carriers in the population.

\(\alpha \) is the probability of contamination of a healthy individual as a result of a contact with a virus carrier per unit time (e.g., per day). This probability is defined as the probability of contamination in a single contact with a virus carrier multiplied by the number of contacts of a individual with all population members per unit time. In the present consideration, \(\alpha \) is a model parameter.

\(P = \alpha \Delta t(N(t) - N(t - \tau )){\text{/}}{{N}_{{\max}}}\) is the probability of contamination during a time interval \(\Delta t\), e.g., during a day, for one individual at a given density of infection carriers.

Then the number of infected during unit time

$$\Delta N = P({{N}_{{\max}}} - N(t)) = ({{N}_{{\max}}} - N(t))\alpha \frac{{(N(t) - N(t - \tau ))}}{{{{N}_{{\max}}}}}\Delta t,$$
(1)

determines an equation for time dependence of the infected individuals number. Thus, we get an equation for the change of the infected individuals number with time:

$$\frac{{\Delta N}}{{\Delta t}} = \alpha ({{N}_{{\max}}} - N(t))\frac{{(N(t) - N(t - \tau ))}}{{{{N}_{{\max}}}}},$$
(2)

or its continuous analog:

$$\frac{{dN(t)}}{{dt}} = \alpha ({{N}_{{\max}}} - N(t))\frac{{(N(t) - N(t - \tau ))}}{{{{N}_{{\max}}}}}.$$
(3)

It is seen that in the model we can use the notion of density rather than the number of population members. Introducing the notation \(N(t){\text{/}}{{N}_{{\max}}} = x(t)\), we rewrite (3) in the form

$$\frac{{dx(t)}}{{dt}} = \alpha (1 - x(t))(x(t) - x(t - \tau )),$$
(4)

independent of the number of population members and applicable to the description of any community (country, city, etc.).

In Eq. (4) there are two model parameters \(\alpha \) and \(\tau \). By merely introducing a “universal time scale” \(\zeta \) in the units of \(\tau \), \(t = \zeta \tau \), Eq. (4) can be rewritten in the form

$$\frac{{dx}}{{d\zeta }} = \alpha \tau (1 - x(\zeta ))(x(\zeta ) - x(\zeta - 1)),$$
(5)

with a single parameter \(\alpha \tau \), which within the definition (see above) represents the number of newly infected population members by one earlier infected individual. It is intuitively clear that if \(\alpha \tau < 1\), then the number of infected individuals in the population will decrease, and if \(\alpha \tau > 1\) it will increase, in full analogy with the kinetics of chain (nuclear) reaction. Note that in [13] the so called logistic factor \((1 - x(\zeta ))\) is set to be 1, which is true only when \(x(\zeta ) \ll 1\).

One more note should be made. Equation (5), as well as Eqs. (4) and (3), in our setting possess an analytical solution. To demonstrate it more clearly, let us introduce the notations

$$x(t) = \left\{ \begin{gathered} {{x}_{0}}(t) = 0,\quad t < 0, \hfill \\ {{x}_{1}}(t),\quad 0 \leqslant t < \tau , \hfill \\ {{x}_{2}}(t),\quad \tau \leqslant t < 2\tau , \hfill \\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \hfill \\ {{x}_{n}}(t),\quad (n - 1)\tau \leqslant t < n\tau . \hfill \\ \end{gathered} \right.$$

Since in such discretization procedure

$${{x}_{n}}(t - \tau ) = {{x}_{{n - 1}}}(t),$$

the equation for \(x(t)\) yields a chain of equations

$$\begin{gathered} \frac{{d{{x}_{1}}}}{{dt}} = \alpha (1 - {{x}_{1}}(t))({{x}_{1}}(t) - 0),\quad {{x}_{1}}(0) = {\text{const}},\quad 0 \leqslant t < \tau , \\ \frac{{d{{x}_{2}}}}{{dt}} = \alpha (1 - {{x}_{2}}(t))({{x}_{2}}(t) - {{x}_{1}}(t)),\quad {{x}_{2}}(\tau ) = {{x}_{1}}(\tau ),\quad \tau \leqslant t < 2\tau , \\ \frac{{d{{x}_{3}}}}{{dt}} = \alpha (1 - {{x}_{3}}(t))({{x}_{3}}(t) - {{x}_{2}}(t)),\quad {{x}_{3}}(2\tau ) = {{x}_{2}}(2\tau ),\quad 2\tau \leqslant t < 3\tau , \\ ......................................................................................... \\ \end{gathered} $$

The equation for \({{x}_{1}}(t)\) involves no time-shifted terms and can be solved explicitly:

$${{x}_{1}}(t) = \frac{{{{x}_{1}}(0)}}{{{{e}^{{ - \alpha t}}} + {{x}_{1}}(0) - {{x}_{1}}(0){{e}^{{ - \alpha t}}}}}.$$

Hence, the equation for \({{x}_{2}}(t)\):

$$\frac{{d{{x}_{2}}}}{{dt}} = \alpha (1 - {{x}_{2}}(t))({{x}_{2}}(t) - {{x}_{1}}(t))$$

belongs to equations of the type

$$\frac{{dy}}{{dt}} = \alpha (1 - y(t))(y(t) - F(t))$$

with known function \(F(t)\), which have analytical solutions. In particular, the solution that satisfies the initial condition \(y({{t}_{0}}) = {{y}_{0}}\), can be written as:

$$y(t) = 1 + \frac{{\exp\left( { - \alpha \int\limits_{{{t}_{0}}}^t {\left( {1 - F(t')} \right)dt'} } \right)}}{{\tfrac{1}{{{{y}_{0}} - 1}} + \alpha \int\limits_{{{t}_{0}}}^t {\exp\left( { - \alpha \int\limits_{{{t}_{0}}}^{t'} {\left( {1 - F(t'')} \right)dt''} } \right)} {\kern 1pt} {\kern 1pt} dt'}}.$$

The analytical solutions presented above are applicable to complete analysis of the pandemic development within the proposed model, but it requires operation with too cumbersome expressions. Without the analysis of a general solution, the only useful feature of this consideration is the following. If the function \(x(t)\), defined piecewise by the solutions on intervals with the duration \(\tau \) is continuous, the derivative \(dx(t){\text{/}}dt\) will be continuous as well, except a single point \(t = \tau \). At this point \(x(t - \tau ) = x(0)\) cannot be zero (for such initial conditions only a trivial solution \(x = 0\) exists), and the derivative, determined by Eqs. (4) or (5), will always have a discontinuity.

Having discussed the possibilities of the analytical solution, then, at this stage of consideration, we will not use it because of its complexity. We will investigate the rather obvious properties of solutions in the linear approximation or analyze the numerical solutions of Eqs. (4) and (5).

3 PRELIMINARY STUDY

3.1 Initial Stage

It is seen that Eq. (4) is nonlinear and nonlocal due to the time-shifted term. However, at the initial stage when only a small part of the population is infected and \(x(t) \ll 1\), Eq. (4) can be analyzed in the linear approximation

$$\frac{{dx}}{{dt}} = \alpha (x(t) - x(t - \tau )).$$
(6)

We start from the beginning of infection, when \(x(t - \tau ) = 0\). In this case Eq. (6) has an exponential solution

$$x(t) = x(0){{e}^{{\alpha t}}}$$
(7)

with the relative increment of the number of infected individuals (e.g., per day, \(dt \approx \Delta t = 1\) day)

$$\frac{{dx}}{x} = \alpha dt\quad {\text{or}}\quad \frac{{\Delta x(t)}}{{x(t)}} = \alpha .$$
(8)

Thus, the coefficient \(\alpha \) determines the relative growth of the number of infected individuals in the beginning of pandemic. Its values amount to \(0.3{-} 0.2\) (see data for any country according to the Hopkins Institute). With the introduction of (self) isolation regime, the coefficient \(\alpha \) decreases and becomes close to \(0.15{-} 0.1\) (Hopkins Institute data again). To understand further change of infection rage it is necessary to analyze Eq. (6) with the retarded term taken into account. Note that the solution

$$x = {{x}_{0}}{{e}^{{\beta t}}}$$
(9)

satisfies Eq. (6), if \(\beta \) satisfies transcendental equations

$$\beta = \alpha (1 - {{e}^{{ - \beta \tau }}}),$$
(10)

which is easily rewritten into an equation for \(z = \beta \tau \):

$$z = \alpha \tau (1 - {{e}^{{ - z}}}).$$
(11)

Therefore, generally, the relative number of infected during a day a few weeks after the beginning of the pandemic will be determined by the parameter \(\beta \):

$$\frac{{\Delta x(t)}}{{x(t)}} = \beta ,$$
(12)

which, in turn, is determined by Eq. (11). For \(\alpha \tau \gg 1\) Eqs. (10) and (11) have solutions \(\beta \approx \alpha \), i.e., the solutions of Eqs. (7) and (9) coincide. Note that at \(\alpha \tau = 3\), \(\beta \approx 0.94\alpha \), and at \(\alpha \tau = 2.6\), \(\beta \approx 0.9\alpha \), i.e., \(\beta \) practically equals \(\alpha \) (within commonly available data from Wikipedia) already at \(\alpha \tau = 2.5\). The second obvious solution of Eq. (10), \(\beta = 0\), gives rise to a constant contribution that can be neglected in the region of the solution exponential growth, except the case, when there is only one solution of Eqs. (10) and (11). The latter takes place when \(\alpha \tau \leqslant 1\). In this case the solution \(\beta = 0\) is unique, and the possibility to stop pandemic at the stage before global infection arises.

3.2 Final Stage

The solution \(x(t) = 1\), i.e., “everybody is infected” satisfies Eq. (4). Moreover, any constant satisfies Eq. (4). Therefore the solution of Eq. (4) may tend to any constant, including those smaller than 1, i.e., the pandemic can be terminated at incomplete infection of the population.

A simple approximation allows estimating the peak of diseases, that is, finding the conditions under which

$$\frac{{{{d}^{2}}x}}{{d{{t}^{2}}}} = 0.$$

For this purpose in Eq. (4) we expand \(x(t - \tau )\) in a Taylor series in terms of \(\tau \):

$$x(t) - x(t - \tau ) \approx \frac{{dx}}{{dt}}\tau - \frac{1}{2}\frac{{{{d}^{2}}x}}{{d{{t}^{2}}}}{{\tau }^{2}},$$

and under the condition of zero second derivative, obtain from Eq. (4) an equation for the peak number of infected individuals \({{x}_{m}}(t)\):

$$1 = \alpha \tau (1 - {{x}_{m}}(t))$$
(13)

or

$${{x}_{m}} = \frac{{\alpha \tau - 1}}{{\alpha \tau }}.$$
(14)

Below, when demonstrating the behavior of \(x(t)\) and \(x'(t)\)), we will see good agreement of \({{x}_{m}}\) from Eq. (14) with realistic calculations, in spite of using rather rough estimate (13). Moreover, noting that the equation for the variable\(y\): \(x = {{x}_{0}} + (1 - {{x}_{0}})y\)

$$\frac{{dy}}{{dt}} = \alpha (1 - {{x}_{0}})(1 - y(t))(y(t) - y(t - \tau )),$$
(15)

coincides with Eq. (4) with the new effective \({{\alpha }_{{{\text{eff}}}}} = \alpha (1 - {{x}_{0}})\), we will consider \(y\) small compared to \(1\), so that the analysis considered above with the solution of the type

$$y = {{y}_{0}}{{e}^{{\beta t}}}$$
(16)

is acceptable. We substitute (16) into (15) and get for \(\beta \) instead of Eq. (11) an equation with the effective \({{\alpha }_{{{\text{eff}}}}}\), i.e.,

$$\beta \tau = \alpha \tau (1 - {{x}_{0}})(1 - {{e}^{{ - \beta \tau }}}),$$
(17)

which at \(\alpha \tau (1 - {{x}_{0}}) \leqslant 1\) has a trivial solution \(\beta = 0\).

Comparing with the condition (13) of passing the peak of diseases, i.e., assuming \({{x}_{0}} = {{x}_{m}}\), the growth of the epidemic can be described by the following scenario: with an increase in the number of cases, the effective constant \(\alpha \tau (1 - {{x}_{0}})\) decreases and reaches \(1\). At this point, the rate of increase in the number of cases reaches a maximum. Further, the epidemic is declining. It is very likely that this stage can be called the inertial period.

4 EXAMPLES OF NUMERICAL SOLUTIONS

4.1 Solutions with \(\alpha \tau > 1\)

For numerical analysis, Eq. (4) was solved using the Euler method with a step of 1 day. Figure 1 shows numerical solutions for the “free flight” situation, when \(\alpha \tau = 2.8 > 1\). This example can illustrate the policy of full immunization of the society because of its total infection. The initial conditions are chosen to equal one millionth of the population (320 for the USA, 140 for Russia, 12 for Moscow, 2.5 for Almaty, etc.). The infection time was taken 14 days, although it may be more reasonable to take 20–30 days.

Fig. 1.
figure 1

(a) Density of the number of infected individuals \(x(t)\) versus time \(t\) (days), (b) absolute growth rate of the infected number density \(dx{\text{/}}dt\), (c) relative growth rate of the infected number density \((dx{\text{/}}dt){\text{/}}x\) at \(\alpha = 0.2\), \(\tau = 14\) days, \(\alpha \tau = 2.8\), \(x(0) = {{10}^{{ - 6}}}\).

Full size image

As a result, the pandemic lasts about 100 days, the peak of morbidity falls on 80–90 days and reaches 40 individuals per 1000 population. Since there are no such number of hospital beds anywhere (according to the WHO [14] website, the number of hospital beds does not exceed 8 per 1000 population even for developed countries), a large number of denials in medical care (and, therefore, multiple lethal outcomes) accompanies this scheme. It is interesting that the relative increment is accompanied by a jump, when on the 14-th day the dependence switches from solution (7) to solution (9), i.e., by a small difference of \(\alpha \) from \(\beta \) (see above about the discontinuity of derivatives at this point).

Note that at \(\alpha \tau = 2.8\), Eq. (14) yields the infection peak at \({{x}_{m}} = 0.64\), i.e., according to Fig. 1a, on the 86-th day of epidemic development. This conclusion is confirmed by Fig. 1b, where the peak occurs on the 82-th day.

4.2 Solutions with \(\alpha \tau < 1\)

To demonstrate the regime of pandemic fading away at \(\alpha \tau < 1\), when a unique solution \(\beta = 0\) of Eq. (10) exists, we present Fig. 2 illustrating the solution of Eq. (4) at \(\alpha = 0.05\), \(\tau = 14\) days, i.e., \(\alpha \tau = 0.7 < 1\). The initial value was chosen \(x(0) = {{10}^{{ - 5}}}\), i.e., 10 times greater than for the calculations shown in Fig. 1. This was done for the convenience of the analysis, since the growth of the number of infected individuals is small. The growth of the number of infected individuals is seen to tend to a constant (nearly 3.5 times) not achieving unity. In other words, it is possible to stop pandemic without total infection of the population. For this purpose, the product \(\alpha \tau \) must be less than one, as discussed above. In this regime, the derivative has a noticeable jump, since \(\alpha \) and \(\beta \) differ considerably. For this example, the pandemic lasts nearly 100 days, which is close to the example shown in Fig. 1. It is an accidental coincidence. Choosing a greater probability of infection, e.g., \(\alpha = 0.07\), we get significantly longer time of pandemic development (about 1500 days) in the \(\alpha \tau < 1\) regime. The number of infected individuals in this case increases by nearly 50 times, i.e., the solution will again tend to a constant different from 1, but during much longer time.

Fig. 2.
figure 2

(a) Density of the number of infected individuals \(x(t)\) versus time \(t\) (days), (b) absolute growth rate of the infected number density \(dx{\text{/}}dt\), (c) relative growth rate of the infected number density \((dx{\text{/}}dt){\text{/}}x\) at \(\alpha = 0.05\), \(\tau = 14\) days, \(\alpha \tau = 0.7\), \(x(0) = {{10}^{{ - 5}}}\).

Full size image

4.3 Dependence of Solutions on the Parameter \(\alpha \tau \)

The considered examples of numerical solutions do not contradict the analysis of Eq. (4) in linear approximation. Moreover, they confirm the basic conclusions. However, it is still unclear how the solution goes to a constant at large times for \(\alpha \tau > 1\). In this case, it is impossible to use the linear approximation for the analysis, and numerical approach should be applied. Since Eq. (5) depends on the only parameter \(\alpha \tau \), below we present numerical solutions at different values of this constant. The correct scheme of displaying the density of infected individuals as a function of the variable \(\zeta \) is not demonstrative, so below we use the time axis in days with \(\tau = 14\) days. For other values of \(\tau \) the quantity \(\tau {\text{/}}14\) is a scaling factor. For example, 100 days at \(\tau = 14\) will become 200 days at \(\tau = 28\). In all calculations, \(x(0) = {{10}^{{ - 6}}}\).

Figure 3 illustrates the kinetics of infection density and its derivative with respect to time \(t\) at different values of \(\alpha \tau < 1\). As seen from Fig. 3a, in the case of \(\alpha \tau < 1\), namely, at \(\alpha \tau = 0.5,\;0.9,\;0.99\), the pandemic stops at small amount of infected individuals (not exceeding 0.01% of the population) but the time of its development is rather long and increases as \(\alpha \tau \) approaches 1. For large \(\alpha \tau \) = 1.5, 2, 3, 5 the fraction of infected population changes from 60 to 100% during rather short times of infection development. Figure 3 also presents solutions at \(\alpha \tau \) slightly exceeding 1. Thus, at \(\alpha \tau = 1.01\) the solution becomes stabilized at a constant level during a long time (years). At \(\alpha \tau = 1.1\) the time of achieving a plateau is shorter, but the proportion of infected will amount to 18%. From Fig. 3b it is seen that at \(\alpha \tau > 1\) the derivative \(dx{\text{/}}dt\) increases in a certain interval at \(t > \tau \), which is not the case at \(\alpha \tau \leqslant 1\). Note that to dateFootnote 1 the number of infected individuals in Russia is 0.13%, in Germany 0.20% in the USA 0.36%, i.e., in these countries the \(\alpha \tau > 1\) scenario takes place.

Fig. 3.
figure 3

Numerical solutions \(x = x(t)\) of Eq. (5) and their derivatives \(dx{\text{/}}dt\) versus \(t\) measured in the units of \(\tau {\text{/}}14\) at different values of \(\alpha \tau \): 0.5, 0.9, 0.99, 1.01, 1.1, 1.5, 2, 3, 5.

Full size image

4.4 Epidemic Waves

The above reasoning shows that for a given constant \(\alpha \tau \), the peak of the disease is determined by Eq. (13), and is the only one. However, if the parameter \(\alpha \tau \) can be controlled, two or even three peaks can be observed. To demonstrate this statement, we introduce a control of the parameter \(\alpha \) with a sharp change in its value:

$$\alpha = {{\alpha }_{0}}(1 + \varepsilon - \varepsilon {{e}^{{ - {{{(t/T)}}^{6}}}}}).$$
(18)

To choose the value of \(\varepsilon \), one can rely on the values of the effective constant \(\alpha \tau (1 - {{x}_{0}})\), which must be greater than 1, and the asymptotic value of \({{x}_{\infty }}\), e.g., from Fig. 3, at \({{x}_{0}} = {{x}_{\infty }}\). Figure 4 illustrates the calculations with the appearance of two or even three peaks. It can be seen that for the selected value of \({{\alpha }_{0}}\tau \) near 1, a small jump in \(\alpha \) by 20% (Figs. 4a, 4b) leads to the appearance of a second peak (Fig. 4b), and in order for them to be observed, the switching time of the parameter \(\alpha \) is \(T = 1500\) days (compare Figs. 4a, 4b). For the third peak to appear, the jump in \(\alpha \) must be greater. In the given example (Fig. 4c), \(\alpha \) increases by 3 times.

Fig. 4.
figure 4

Absolute growth rate \(dx{\text{/}}dt\) of the infected number density versus time \(t\) measured in the units of \(\tau \): (a) for \(T = 1100\) days and \(\alpha = {{\alpha }_{0}}(1.2 - 0.2\exp( - {{(t{\text{/}}T)}^{6}}))\), (b) for \(T = 1500\) days and \(\alpha = {{\alpha }_{0}}(1.2 - 0.2\exp( - {{(t{\text{/}}T)}^{6}}))\), (c) for \(T = 1500\) days and \(\alpha = {{\alpha }_{0}}(3 - 2\exp( - {{(t{\text{/}}T)}^{6}}))\) , \({{\alpha }_{0}}\tau = 1.1\), \(\tau = 14\) days, \(x(0) = {{10}^{{ - 6}}}\).

Full size image

The choice of the transition function in the form (18) is rather arbitrary, and it is possible to study functions with a faster degree of switching of the value of \(\alpha \tau \), thus compressing the time scale for the emergence of new peaks of the disease. It is for this behavior that society’s response to the pandemic is responsible.

Thus, the answer to the question of whether we can expect two or more peaks in the rates of the disease can be formulated so: “The number of peaks can reach at least three, and is determined by the amplitude and rate of change in the parameter α”.

4.5 Infection Transport

Considering the development of a pandemic within the framework of Eqs. (4)–(5), i.e., within the scheme “an infected patient charges others”, we did not take into account the influx of infected patients from the outside. While for large communities, this growth mechanism of infected number may turn out to be insignificant, for small cities the influx of ill individuals from outside can have a significant impact on the dynamics of infection development. In order to include the flow of infected in Eqs. (4) or (5), one can simply add the term \(j\) to the derivative \(\tfrac{{dx}}{{dt}}\):

$$\frac{{dx}}{{dt}} = \alpha (1 - x(t))(x(t) - x(t - \tau )) + j,$$
(19)

where \(j\) is the relative number of infected individuals arriving at the community per unit time, e.g., per day. Generally, the flux of infected individuals \(j\) is a function of time and can be easily changed due to social efforts up to complete isolation (\(j = 0\)).

When considering the infection development with Eq. (19), the initial condition \(x(t = 0)\) can be zero, if we remove the discontinuity of derivative at \(t = \tau \) mentioned above. The schemes used for analyzing Eq. (4) are also applicable to Eq. (19). Instead of repeating them, we present an example of a numerical solution of Eq. (19), displayed in Fig. 5 at relatively small values of \(\alpha \tau \) and \(j\). The chosen value \(j = {{10}^{{ - 6}}}\) means that one infected individual arrives at a city with a population of 100 000 during 10 days. As seen from Fig. 5, even such insignificant inflow of infected individuals leads to a burst of infection that develops faster than when the initial number of infected individuals is set. This can be seen from comparison of Fig. 5 with the curve for \(\alpha \tau = 1.1\) in Fig. 3a.

Fig. 5.
figure 5

(a) Infected number density \(x(t)\) versus time \(t\) measured in the units of \(\tau \), and (b) the absolute growth rate \(dx{\text{/}}dt\) of the infected number density at \(\alpha \tau = 1.1\), \(\tau = 14\) days, \(x(0) = 0\), \(j = {{10}^{{ - 6}}}\).

Full size image

A characteristic feature of the dynamics of diseases in the case of an external influx of infection carriers is an “extending tail”, which, in principle, allows seeing the source of diseases in the external influx of carriers of the infection.

5 COMPARISON OF THE CURRENT MODEL WITH THE SIR MODEL

As noted above, the Spanish flu pandemic provoked the need to create a pandemic forecast based on, albeit simplified, but mathematical models. In particular, it was then that the still used SIR model was created [5]. At present, this model has been significantly expanded, but its equations are still basic, and it is with them that we will compare the present model.

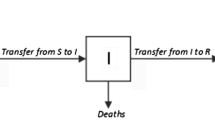
The model name is an abbreviation for three model variables: \(S\)—Susceptible (the number of people who can become infected), \(I\)—Infectious (the number of carriers of the infection), R—removed (the number of people not able to become infected (immune or dead)). The system of differential equations, dating back to [5], is written in the form:

$$\frac{{dS}}{{dt}} = - \frac{{\alpha IS}}{{{{N}_{{\max}}}}},$$
(20)
$$\frac{{dI}}{{dt}} = \frac{{\alpha IS}}{{{{N}_{{\max}}}}} - \gamma I,$$
(21)
$$\frac{{dR}}{{dt}} = \gamma I.$$
(22)

Here, \({{N}_{{\max}}}\) is the number of population members, \(\alpha \) and \(\gamma \) are the model parameters. The system of equations (20)–(22) preserves the total number of population members in time, i.e., \(S + I + R = {{N}_{{\max}}}\). To compare our model with the SIR model, let us express the SIR variables in our notation. Thus, our \(N(t)\) is the number of infected, then \(S = {{N}_{{\max}}} - N(t)\), \(R = N(t - \tau )\), \(I = N(t) - N(t - \tau )\). Substituting thus expressed variables \(S\), \(I\), and \(R\) into Eqs. (20)–(22) we get:

$$\frac{{d({{N}_{{\max}}} - N(t))}}{{dt}} = - \frac{{\alpha ({{N}_{{\max}}} - N(t))(N(t) - N(t - \tau ))}}{{{{N}_{{\max}}}}},$$
(23)
$$\frac{{d(N(t) - N(t - \tau ))}}{{dt}} = \frac{{\alpha ({{N}_{{\max}}} - N(t))(N(t) - N(t - \tau ))}}{{{{N}_{{\max}}}}} - \gamma (N(t) - N(t - \tau )),$$
(24)
$$\frac{{dN(t - \tau )}}{{dt}} = \gamma (N(t) - N(t - \tau )).$$
(25)

Evidently, Eq. (23) is exactly Eq. (3) of our model, and when using densities, Eq. (4). Equation (24) with Eq. (25) taken into account also yields Eq. (3). Since Eq. (3) and following from it Eqs. (4) and (5) have unique solutions, formally Eqs. (22) and (25) serve only to relate parameters \(\gamma \) and \(\tau \). Naturally, parameter \(\gamma \) can in this case be a function of time, which does not contradict neither the SIR model, nor the condition \(\tfrac{{dS}}{{dt}} + \tfrac{{dI}}{{dt}} + \tfrac{{dR}}{{dt}} = 0\).

Thus, the equation of our model does not contradict the SIR model, being its implementation with a  functional relationship between the numbers of ill individuals and carriers of infection \(I = N(t) - N(t - \tau )\).

6 ANALYSIS OF THE CURRENT SITUATION

Now it is accepted that the COVID-19 antibodies appear in virtually all patients in 20–24 days after infection. Therefore, in this analysis we assume the infection time \(\tau \) to be 21 days in a society, where the anti-infection measures do not allow its radical reduction (“free regime”). With the assumed probability of contamination in the (self) isolation regime \(\alpha = 0.1{-} 0.15\), we get \(\alpha \tau = 2.2{-} 3.15\), which yields (see Fig. 3 for \(\alpha \tau = 2,\;3\)) the time of population infection of about 150 days with the natural pandemic (February-June) termination in late June–July 2020 in virtually all countries after the first infective episode in China. If the community will manage to reduce the infection time \(\tau \) by 2–3 times, the duration of pandemic will increase to a few years with a “bonus” of lower number of ill individuals.

Naturally, the protection measures aimed at reducing \(\alpha \tau \) will make it necessary to solve Eqs. (4) with variable \(\alpha \tau \), and the presented numerical solutions will not represent the situation to the full extent. In this case, for the aim of prognosis one can solve the equations “at the current moment of time”. To do so, the knowledge of \(\alpha \tau \) at the current time is necessary. Note that due to the social measures the values of \(\alpha \tau \) became closer to 1, and the observed increase of the number of infected individuals is determined by the parameter \(\beta \), i.e., the solution of Eq. (10). For \(\alpha \tau \) approaching 1, it is possible to point out a linear relation between these parameters

$$\alpha \tau \approx 1 + \beta \tau {\text{/}}2.$$
(26)

For example, in the USA, where the number of infected individuals achieved 0.4% (16.05.2020) the daily increment amounts to about 2%. For \(\tau = 21\) days \(\alpha \tau = 1.21\). In the pandemic development mode, according to Fig. 3 for \(\alpha \tau = 1.1,\;1.5\), the duration of pandemic is expected to be not less than a year. If the low increment of infection is due to the pandemic termination, the number of infected individuals should be much beyond the official statistics. In fact, the choice of pandemic development scenarios is rather limited: either the major part of the population is already infected (beyond the official statistics), or the pandemic will last a year or more.

Figure 6 presents the data from Wikipedia on the number of COVID-19-infected people in Moscow and the parameter \(\alpha \tau \equiv \alpha (t)\tau \) calculated based on these data according to Eq. (2):

$$\alpha \tau = \frac{{\tau (N(t + 1) - N(t))}}{{(1 - N(t){\text{/}}{{N}_{{\max}}})(N(t) - N(t - \tau ))}}$$
(27)

at \(\tau = 21\) days. From Fig. 6 it is seen that until mid-May \(\alpha \tau \) decreases, which is due to both the gradual introduction of restrictions and the understanding of the situation by the citizens. A jump of \(\alpha \tau \) near May 1 is caused by the fact that on April 15 checking passes at the entrance to the Moscow metro accumulated crowds of people, which gave favorable conditions for the spread of the virus. Beginning from the mid-May till the end of June \(\alpha \tau \approx 0.55{-} 0.8\) becomes constant, and there is a decrease in the daily increment in the number of infected individuals. In mid-June the restrictions in Moscow are gradually removed, and in the first two decades of July a growth of \(\alpha \tau \) is observed. From the end of July till mid-August \(\alpha \tau \approx 1.05{-} 1.1\) and the daily increment of the infected people number amounts to about 700, however, using these data for modeling yields a pessimistic result: by the end of the year, the daily increase will exceed 1000 people, and the number of cases will be 350 000.

Fig. 6.
figure 6

(a) The number of individuals infected by COVID-19 \(N(t)\), (b) the daily increment of infected people number \(\Delta N(t)\) from March 2 to August 13 in Moscow (according to the data available from Wikipedia), (c) time dependence of the parameter \(\alpha \tau \equiv \alpha (t)\tau \) from April 1 to August 13 with \(\tau = 21\) days.

Full size image

Relatively even distribution of infected people in Moscow by the beginning of the epidemic and the slow propagation, when a person infected at one end of Moscow can infect other people at another end, as well as regulations (laws) that do not depend on a particular district of Moscow, make it possible to neglect the focality and consider the entire metropolis as one population. A large number of patients minimize the probabilistic component of the error, which can be seen in the Figs. 6, 7, where the amplitude of rapid fluctuations in the daily increase in patients and the product \(\alpha \tau \) decrease with time.

Fig. 7.
figure 7

(a) Time dependence of parameter \(\alpha \tau \equiv \alpha (t)\tau \) from April 1 to August 13 for Moscow with \(\tau = 7,\;14,\;21,\;28\) days; (b) number of infected people \(N(t)\), and (c) daily increment of the infected people number \(\Delta N(t)\), obtained by extrapolating to 2021–2024.

Full size image

For illustration, Fig. 7 presents the model parameter \(\alpha \tau \equiv \alpha (t)\tau \) with \(\tau = 7,\;14,\;21,\;28\) and the forecast of the number and daily increase of infected, obtained using the average value of \(\alpha \tau \equiv \alpha (t)\tau \) from July 31st to August 13th. For all \(\alpha \tau \), there is an increase in the daily increase in infected. Moreover, for \(\tau < 14\), the jump of \(\alpha \tau \) in the vicinity of May 1 becomes inexplicable.

7 CONCLUSION. DRAWBACKS OF THE MODEL

The proposed two-parameter model of the development of infection in the form of an ordinary nonlinear differential equation of the first order with retarded time argument is actually a reduced SIR model with a functional relationship between patients and carriers of the infection \(I = N(t) - N(t - \tau )\). This reduction maintains an optimal balance between the adequacy of describing a pandemic in the SIR model and the simplicity of practical estimates. In this case, the proposed model allows solving both the direct problem, i.e., for given parameters \(\tau \) and \(\alpha \) find the dependence of the density of infected \(x(t)\) on time \(t\), and the inverse problem, i.e., for a given dependence of the density of infected on time, determine the dependence of the model parameters on time. This makes it possible to quickly predict the development of infection based on previous information on the statistics of the disease (see Fig. 7).

Note that for a given constant \(\alpha \tau \) the peak of the disease is determined by Eq. (13) and is unique. However, with the possibility of a sharp change in the parameter \(\alpha \tau \), two or even three peaks can appear, as shown in Fig. 4. Such a change in \(\alpha \tau \) due to varying \(\alpha \) may be related to a seasonal dependence of susceptibility to disease or depend on the number of contacts on weekdays, holidays, and vacations. In particular, for Russia, the minimum value of \(\alpha \tau \) fell on the spring and summer holidays and can be expected during the autumn and winter vacations. Changes in the value of \(\alpha \tau \) due to the parameter \(\tau \) are largely determined by the reaction of society to the disease. Thus, the answer to the question whether we can expect two or more peaks in disease rate can be formulated so: “The number of peaks can reach at least three, and is determined by the amplitude and rate of change of the parameter \(\alpha \tau \)”. Current information confirming the multi-peak spread of COVID-19 in megalopolises is presented, e.g., in the messages of RIA Novosti [17].

Considering the development of a pandemic in the framework of Eqs. (4), (5), that is, in the scheme “an infected patient infects others”, we did not take into account the influx of infected persons from the outside. While for large communities this mechanism may turn out to be insignificant, for small cities the influx of patients from the outside can have a significant impact on the dynamics of the infection development. In order to include the flow of infected in Eqs. (4) or (5), it is enough to add the term \(j\) (the relative proportion of infected patients arriving in the community per unit of time) to the derivative \(x(t)\) and as a result get the inhomogeneous equation (19). In the general case, the flow of infected patients \(j\) is a function of time \(t\) and can be easily changed by the efforts of society, up to complete isolation (\(j = 0\)). Figure 5 shows that even a small influx of infected people leads to a disease outbreak that proceeds faster than when imposing the initial condition on the number of patients.

A drawback of the model is description in average. Examples of incorrectness of such a description can manifest themselves in small societies, where the external feeding of infection can play a more important role than the mechanisms of development described by Eq. (4). Besides, the description is independent of coordinates, i.e., does not reflect the spatial distribution of the infection over a territory. Therefore, the subsequent infection bursts due to the leveling of the infected density over regions are beyond the model. The rest drawbacks related to the number of model parameters (e.g., division of population into groups, each having its own value of \(\alpha \tau \)), seem to be of minor importance for the description of population in whole. An essential feature of COVID-19 that makes it a somewhat unique among other infections is that the severity of disease strongly differs in individual patients from easy to mortal outcome. Moreover, in the course of the disease development there is a singular (bifurcation-like) point at which the fatal lung complications unexpectedly occur in some patients. These features are of great practical significance since the easy cases strongly underestimate the statistics (the patients do not seek medical aid and are not taken into account), while the potentially dangerous cases need special immediate care. In the present simplified model, these features, the nature of which is still far from clear [18] were not included. A challenge for future studies is to remove the above drawbacks striving to maintain the optimal balance between model adequacy and simplicity for practical evaluations.