Abstract
We use a simple general model of interactive dynamics between the COVID-19 pandemic and the economy to examine the impact of various non-pharmaceutical interventions in the form of restrictions on socio-economic activities like lockdowns, travel restrictions, etc. We mathematically demonstrate that these restrictions might be useful in preventing repeated waves of infection recurrence in the pandemic. These results are general and not dependent on choice of specific functional forms or parameter configurations. We set out briefly the implications of these results for public health interventions.
Similar content being viewed by others
1 Introduction
Using a generalized model of interactive dynamics between the epidemiological and the economic processes that results in the spread and transmission of the COVID-19 pandemic, this paper attempts to assess the efficacy of non-pharmaceutical interventions like restrictions on economic activities and travel. A broad motivation, underlying this paper, is to develop an analytical framework which does not depend on the choice of specific functional forms or estimation of the numerical parameters of the model to examine the COVID-19 pandemic.
The current COVID-19 pandemic has revived a large interest in the classical epidemiological models [1, 2, 18, 20, 28, 36], first proposed by Kermack and McKendrick [19]. An important feature of these early models, which classified the population into three categories namely susceptible, infected and recovered (SIR), is that the infected people who recover acquire lasting immunity. In other words, the section of population which has recovered can no longer move back to the infected group. It is possible, therefore, in this class of models for the pandemic to converge to zero infection, even in the absence of public health policy intervention, when a substantial proportion of population acquires immunity through infection. In other words, the population, under certain circumstances, acquires spontaneous herd immunity, though this might come at the cost of a high death toll.
For COVID-19, however, re-infections have been common either because immunity based on antibodies (among the previously infected) fades with time or because antibodies acquired during recovery against one variant of SARS-CoV-2 may not be effective (either wholly or partially) against other variants. Hence, till the vaccines became widely available and are administered rapidly so that a significant proportion of the population is vaccinated (resulting in vaccine based herd immunity ahead of newer current vaccine resistant variants emerging), the policymakers have perforce relied on various non-pharmaceutical interventions in the form of restrictions on economic activities and other activities including travel in order to try and control the pandemic. Consequently, a line of literature has emerged which incorporates these non-pharmaceutical interventions in the traditional compartmental models; for instance, Ngonghala et al. [29] found that these interventions are effective in achieving the disease-free equilibrium, but early termination of these measures might lead to devastating recurrent waves of infections. These restrictions, however, in addition to influencing the spread of the pandemic, also have adverse economic impacts, often compelling the policymakers to periodically withdraw these restrictions [8, 22, 33, 37, 38], leading to a resurgence of the pandemicFootnote 1. Many traditional epidemiological models do not capture this interaction between the epidemiological and the economic processes. A new class of models came up recently which attempts to capture the joint interactive dynamics of the epidemiological and the economic processes. Eichenbaum, Rebelo, and Trabandt [10, 11] represent early examples in this direction, where representative agents from each of the different categories of the SIR model optimize the lifetime utility function of consumption and leisure in infinite horizon. More recent contributions include [16, 30]. Boucekkine et al. [4] contains a comprehensive review of the recent literature. A line of recent literature also looks at the role played by imperfect information about the pandemic from the point of view of both the policymakers and households [12,13,14, 14].

Source:World Health Organization COVID-19 Dashboard https://worldhealthorg.shinyapps.io/covid/
Multiple waves in New Cases and New Deaths.
The framework in much of this literature, however, is based on either analytical models with specific functional forms, or on numerical simulation based on estimated numerical values of the parameters of the model. This approach is, without any doubt, helpful in creating testable models which can also be used for forecasting or predicting the future course of the pandemic. The validity of these models, however, depend critically on estimation of the various functional forms as well as estimation of the parameters of these models. We adopt an alternative approach in this study, by proposing a general model of interactive dynamics between the epidemiological and economic processes. We feel that this exercise makes an important contribution to the existing literature since qualitative properties which are largely independent of parameter values (which are themselves rapidly changing during the course of the pandemic) are important to arrive at appropriate public health policy interventions. To the best of our knowledge, this is the first such attempt at providing a general framework of the interaction between the epidemiological and economic processes underlying the spread of the pandemic and the policy interventions to control it.
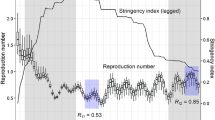
The broad stylized facts on the spread of the pandemic in many countries demonstrate, contrary to the convergence to no-infection steady state predicted by the traditional epidemiological models, that there have been multiple cycles or waves of infections. These waves are often accompanied with (and perhaps induced by) policy cycles of imposition and gradual easing of restrictions on economic activities; see, for instance, Fig. 1 for a graphical demonstration of this feature in Italy and Spain, two of the earliest sites of the outbreak; Sweden, notable for its unorthodox policy characterized by lack of strict lockdowns and other restrictions to deal with the pandemic [5]; and India which is currently in the middle of a severe second wave, even after the government publicly claimed success at controlling it after the first wave [32, 35].
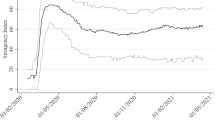
Nason [27] explored these cycles in greater detail using Bayesian spectral fusion methods, and found that many countries have already gone through at least three cycles. However, some countries seem to have escaped this kind of cyclical behavior so far. China, the first site of reported infection as well as its epidemiological spread, has not shown the waves of resurgence that we noticed in several other countries. This can be seen below in Fig. 2:
It is our contention that such persistent cyclical behavior is possible only when these cycles are generated endogenously through the interaction between the epidemiological and the economic processes in the context of the socio-economic-political regimes in these countries. The existing literature, to the best of our knowledge, does not examine this aspect in much detail. In our view, this represents a gap in the existing literature on the COVID-19 pandemic, which we attempt to address in the current study. We believe that a generalized framework, which we attempt to construct in this study, is the most appropriate to examine these questions as the results therein will not depend on specific idiosyncracies like the choice of the functional form or the numerical values of the parameters of the model.
We begin in Sect. 2 with a general model to represent the onset of the pandemic. We proceed then in Sect. 3 with a model which captures the effect of the non-pharmaceutical policy interventions.

Source:World Health Organization COVID-19 Dashboard https://worldhealthorg.shinyapps.io/covid/
China: Lack of waves in new cases and new deaths.
2 Onset of the pandemic
2.1 Basic setup
Consider a general model of a closed economy at the onset of the pandemic. The level of economic activities at time t, \(y \in \mathfrak {R}_{+} \), adjusts by standard argument of convergence in growth models to some long-run equilibrium level (which need not necessarily involve full utilization of economic resources). The arrival of the COVID-19 pandemic, however, disrupts the production process (both by affecting the health of the workers as well as inducing restriction on economic activities by the policymakers) and negatively affects this process of adjustment. We represent this with the continuously differentiable function, f, as follows:
where i is the proportion of the total population who are infected with COVID-19, and \(\alpha >0\) is a speed of adjustment parameter, representing slow adjustment of the agents as they learn about the pandemic. \({\partial f}/{\partial i}\) depends, among other things, on the policy environment. The more quickly the policymaker responds to the spread in the pandemic with restrictions on economic activities, higher will be the sensitivity of economic activities to the rate of infection (resulting in a larger negative value of \({\partial f}/{\partial i}\).)
Next, we turn our attention to the dynamics of spread of COVID-19. Much of the existing literature largely relies on some version of early epidemiological models proposed, among others, by Kermack and McKendrick [19], which divides the population into various compartments like the susceptible, the infected and the recovered. However, we seek to develop a more general framework that does not depend on specification of functional forms, and also captures the interaction between the economic and the epidemiological processes. We assume, not implausibly, that the population is divided into only two categories namely the susceptible and the infected. Further we also assume for simplicity that the population does not change in the period under consideration. Lastly, we argue that a rise in economic activity, other things remaining the same, increases the share of the infected in the population due to an increase in interaction between the (possibly asymptomatic) infected and the susceptible persons. These considerations allow us to suggest the following general form:
where g is continuously differentiable and \(\beta >0\) is a speed of adjustment parameter. \({\partial g}/{\partial y}\) is the sensitivity of the rate of infection to increase in economic activity.
Equations (1) and (2) might be considered together as a system of differential equations, representing the dynamic interaction between the economic activities and the spread of infection in the economy. The economic activities positively affect the epidemiological process of spread of the pandemic by increasing the number of interactions between the infected and the susceptible persons. The spread of infection, on the other hand, negatively affects the economic activities in two ways; firstly by affecting the health of the workers, and secondly, by inducing the policymakers to bring in various types of restrictions on economic activities. The extent of policy response will depend on various socio-economic and political factors. However, very few governments will willing to allow the pandemic to spread unchecked without bringing in any restrictions on socio-economic activities.
We should point out here that in specifying the general dynamical system in (1) and (2) we have not imposed any additional restrictions other than the ones required to describe our story of the emerging pandemic. In particular, we have neither assumed any specific functional form for f or g, nor imposed restrictions on the second and higher order derivatives of f and g so far.
2.2 Equilibria and local stability
It is easy to see that the dynamical system represented by (1) and (2) has four types of equilibria: (a) Trivial Equilibrium \(E_1: ( 0, 0 )\), where both economic activities and infections collapse to zero; (b) ‘Good Health Equilibrium’ \(E_2: ( {\bar{y}}_2, 0 )\), where economic activities can continue with no infected persons; (c) Non-Trivial Equilibrium \(E_3: ( {\bar{y}}_3, {\bar{i}}_3) \), where economic activities continue with a certain proportion of population remaining infected; and (d) ‘Bad Equilibrium’ \(E_4: ( 0, \bar{i}_4 )\), where economic activities collapse even as a certain proportion of the population remains infected.
We note that in general, multiple equilibria are possible only for the type \(E_3\). Next, we propose the following:
Lemma 1
\(f (y,i ) = 0\) as defined in (1) is downward-sloping and intersects the y-axis and the i-axis at \({\bar{y}}_2\) and \({\hat{i}}\) respectively; similarly, \(g (y,i) =0\) as defined in (2) is downward-sloping and intersects the y-axis and the i-axis at \({\hat{y}}\) and \({\bar{i}}_4\) respectively; \( \bar{y}_2, {\hat{y}}, {\bar{i}}_4, {\hat{i}} \in \mathfrak {R}_{+}\).
Proof
First, we note from (1) that \(\partial f / \partial y <0\) and \( \partial f / \partial i<0\), so it follows that along the curve \(f(y,i)=0\), we have \({di}/{dy}|_{f (y,i) =0} = -(\partial f / \partial y)/(\partial f / \partial i) < 0 \), which also gives us the slope of \(f(y,i)=0\). Similarly, we note from (2) that \(\partial g / \partial y>0\) and \(\partial g / \partial i>0\), so it follows that along the curve \({g (y,i) =0}\), we have \({di}/{dy}|_{g (y,i) =0} = - (\partial g / \partial y) / (\partial g / \partial i) <0 \), which also provides us with the slope of \({g (y,i) =0}\). Taken together, this implies that both \(f (y,i ) = 0\) and \(g (y,i)= 0\) are downward-sloping. Further, given that \(f (0,0) >0\) and \(\partial f / \partial y, \partial f / \partial i <0\), from continuous differentiability of f it follows that \(\exists \ \bar{y}_2 \in \mathfrak {R}_{+} \ni f ({\bar{y}}_2, 0) = 0\), and \(\exists \ {\hat{i}} \in \mathfrak {R}_{+} \ni f (0, {\hat{i}}) = 0\), i.e. \(f(y,i)=0 \) intersects y and i axes in the non-negative quadrant. Similarly, given that \(g (0,0) <0\) and \(\partial g / \partial y >0 \) and \(\partial g / \partial i >0\), from continuous differentiability of g it follows that \(\exists \ {\hat{y}} \in \mathfrak {R}_{+} \ni g ({\hat{y}}, 0) = 0\) and \(\exists \ {\bar{i}}_4 \in \mathfrak {R}_{+} \ni g (0, {\bar{i}}_4) = 0\), i.e. \(g(y,i)= 0 \) intersects y and i axes in the non-negative quadrant. \(\square \)
Corollary 2.1
For the dynamical system represented by (1) and (2), \(E_1\), \(E_2\) and \(E_4\) will always exist in the non-negative quadrant.
Proof
Follows from lemma 1. \(\square \)
Lemma 2
\(( {\hat{y}} - {\bar{y}}_2 ) ( {\hat{i}} - {\bar{i}}_4 ) >0\) is a sufficient condition for \(E_3 \in {\mathop {{\mathrm{int}}}} \mathfrak {R}^2 _{++} \).
Proof
\(( {\hat{y}} - {\bar{y}}_2 ) ( {\hat{i}} - {\bar{i}}_4 ) >0 \ \Leftrightarrow \) either \({\hat{y}}> {\bar{y}}_2\) and \({\hat{i}} > {\bar{i}}_4\) or \({\hat{y}}< {\bar{y}}_2\) and \({\hat{i}} < {\bar{i}}_4 \ \Leftrightarrow \) \(f (y,i ) = 0\) and \(g (y,i)= 0\) must intersect each other at least once inside the non-negative quadrant. Hence it follows that there must be at least one interior non-trivial equilibrium represented by \(E_3\). \(\square \)
Lemma 3
For the dynamical system represented by (1) and (2): (a) the Trivial Equilibrium, \(E_1\) is a saddle-point; (b) the ‘Good Health Equilibrium’, \(E_2\) is either locally stable or saddle-point; (c) any non-trivial equilibrium, \(E_3\) (if it exists in \(\mathfrak {R}_{+} \times \mathfrak {R}_{+}\)) is a saddle-point if \(f(y,i) = 0\) is steeper than \(g(y,i) = 0\) at the point of intersection at \(E_3\); and is either stable or unstable otherwise; and (d) The ‘Bad Equilibrium’, \(E_4\) is either saddle-point or locally unstable.
Proof
Let \(J_1\), \(J_2\), \(J_3\) and \(J_4\) be the jacobian of the dynamical system represented by (1) and (2) evaluated at \(E_1\), \(E_2\), \(E_3\) and \(E_4\) respectively. Next, we note the following:
-
(a)
at \(E_1\), we have the determinant, \( \det (J_1) = \alpha \beta f \left( 0, 0 \right) g \left( 0, 0 \right) < 0\). Hence \(E_1\) is always saddle-point.
-
(b)
Next, at \(E_2\), for \(0< {\bar{y}}_2< {\hat{y}} \Leftrightarrow g \left( {\bar{y}}_2,0 \right) <0\), we have the determinant \(\det (J_2) = \alpha \beta (\partial f / \partial y) {\bar{y}}_2 g \left( {\bar{y}}_2 , 0 \right) >0\) and the trace, \(\text {trace} (J_2) = \alpha (\partial f / \partial y) {\bar{y}}_2 + \beta g \left( {\bar{y}}_2, 0 \right) <0\), i.e. \(E_2\) is locally stable. For \({\bar{y}}_2> {\hat{y}}>0 \Leftrightarrow g \left( {\bar{y}}_2,0 \right) >0\), we have the determinant, \(\det (J_2)<0\), i.e. \(E_2\) is a saddle-point.
-
(c)
Next, we turn to non-trivial equilibrium, \(E_3\), when it exists inside real positive orthant, i.e. \(E_3 \in \mathfrak {R}_{+} \times \mathfrak {R}_{+}\). The determinant, \(\det (J_3) = \alpha \beta {\bar{y}}_3 \bar{i}_3 \left( \frac{\partial f}{\partial y} \frac{\partial g}{\partial i} - \frac{\partial f}{\partial i} \frac{\partial g}{\partial y} \right) <0\) for \(- \frac{\partial f / \partial y}{\partial f / \partial i }< - \frac{\partial g / \partial y}{\partial g / \partial i } \Leftrightarrow \left( di / dy \right) _{f(y,i)=0} < \left( di / dy \right) _{g(y,i)=0}\), i.e. between the two negatively sloped curves, \(f(y,i)=0\) has a higher slope than \(g(y,i) = 0\) at the point of intersection. On the other hand, if \(g(y,i) = 0\) has a higher slope than \(f(y,i)=0\) at the point of intersection, i.e. \(\det (J_3) >0\), then \(\text {trace} (J_3) = \alpha (\partial f / \partial y) {\bar{y}}_3 + \beta (\partial g / \partial i) {\bar{i}}_3 < 0 \) for \(\left( \alpha / \beta \right) > - \left[ (\partial g / \partial i) {\bar{i}}_3 \right] / \left[ (\partial f / \partial y) \bar{y}_3 \right] \). In other words, the non-trivial equilibrium is stable if the economic process adjusts faster than the adjustment of the pandemic dynamics.
-
(d)
Finally, at the ‘Bad Equilibrium’, \(E_4\), for \(0< {\bar{i}}_4 < {\hat{i}} \Leftrightarrow f \left( 0, {\bar{i}}_4 \right) > 0\), we have \(\det (J_4) = \alpha \beta (\partial g / \partial i) {\bar{i}}_4 f \left( 0, {\bar{i}}_4 \right) >0\) & \(\text {trace} (J_4) = \alpha f \left( 0, {\bar{i}}_4 \right) + \beta (\partial g / \partial i) \bar{i}_4 >0\), i.e. \(E_4\) is locally unstable. For \({\bar{i}}_4> {\hat{i}} >0 \Leftrightarrow f \left( 0, {\bar{i}}_4 \right) <0\), we have \(\det (J_4) <0\), i.e. \(E_4\) is a saddle-point.
\(\square \)
Next, we define the critical value of the adjustment parameter, \(\alpha \):
Further, we note the following:
Corollary 2.2
If the non-trivial equilibrium, \(E_3\), exists in the real positive orthant and is not saddle-point, then it undergoes non-degenerate Andronov-Hopf bifurcation at \(\alpha = {\hat{\alpha }}\), leading to emergence of limit cycles around \(E_3\).
Proof
It is clear from proof to lemma 3 that \(\alpha = {\hat{\alpha }} \Leftrightarrow \text {trace} (J_3) = 0 \); further, \(\partial \left( \text {trace} \right) / \partial \alpha = (\partial f / \partial y) {\bar{y}}_3 < 0 \ \forall \ E_3 \in \mathfrak {R}_{+} \times \mathfrak {R}_{+}\), i.e. the derivative exists, and is smooth and continuous. This completes the proof. \(\square \)
Corollary 2.3
If the non-trivial equilibrium, \(E_3\), exists in the real positive orthant and is not saddle-point, then it is locally stable for \(\alpha > {\hat{\alpha }}\).
Proof
From proof to lemma 3 and corollary 2.2, \(\alpha > {\hat{\alpha }} \Leftrightarrow \text {trace} (J_3) <0\), and \(\det (J_3) >0\), so \(E_3\) is locally stable. \(\square \)
We might note from above discussion that the ‘Good Health Equilibrium’, \(E_2\) might not always be attainable, in case the dynamics of the epidemiological process turns it into a saddle-point. In this case, the solution cannot converge to a steady state with no infection. We further note that in case the solution does not converge to the ‘Good Health Equilibrium’, the next best option might be for the solution to converge to a non-trivial equilibrium, which requires the economic processes to adjust faster than the pandemic dynamics. However, without placing any additional restrictions on the higher order derivatives, we cannot make any further conclusion about the uniqueness or stability of the interior non-trivial equilibria. This will involve, among other things, a consideration of public health policy interventions to which we now turn.
3 Pandemic dynamics with travel restrictions and lockdowns
3.1 Modified general model
When the outbreak of COVID-19 was first detected in Wuhan and other cities of the Hubei province in China, the government responded to it with an effective lockdown (in the form of restrictions on travel and economic activities) in the centers of outbreak of the epidemic, in an effort to quarantine the affected areas [34]. WHO described this lockdown as “unprecedented in public health history” [7]. Subsequently this method of containing the pandemic was sought to be replicated in many countries around the world, but with varying degrees of success. In many countries, the implementation of lockdown measures was ineffective, and associated with several kinds of policy frailties. For instance, in Italy, initial announcement of lockdown in the affected region of Lombardy resulted in large-scale movement of population before the lockdown could be fully put in place [15]. Similarly, in India, there were large-scale movement of migrant workers who lost their jobs due to the lockdown, effectively rendering the lockdown less effective [21]. As mentioned before, these problems arose due to the socio-economic-political regime within which these processes played out.
We begin by looking at how these restrictions work in controlling the pandemic. The pandemic spreads primarily through interaction (either economic or other social) between the infected and the uninfected persons who are susceptible to infection [23]. Policy restrictions on travel and certain types of economic and social activities, if effective, prevent new interactions from taking place, keeping interactions limited within various particular communities in an area. Within these particular communities, even in the absence of additional public health measures, any increase in the proportion of the infected persons, by definition, will reduce the number of susceptible persons. Thus, with an increase in the proportion of infected persons, the rate of growth of new cases of infection (which depends on the number of interactions between infected and susceptible persons) will eventually come down. In other words, a rise in infection is limited by the availability of susceptible persons within a community. This limitation could be circumvented by interaction of infected persons from this particular community with susceptible persons from other communities.Footnote 2 Imposition of restrictions on travel and non-essential economic activies are meant to effectively restrict this process, making the availability of the susceptible persons a limiting constraint on growth of new infections.
For the purpose of formal modeling of the aforementioned process, we represent the evolution of the pandemic within a quarantined community by slightly perturbing the conditions in (2); the modified version is provided below in (4).
The main difference between the formulations in (2) and (4) (and therefore, between the two models in Sects. 2 and 3) is in the sign of the partial derivative, \(\partial g / \partial i\), representing the sensitivity of the rate of change in the proportion of infected persons in the population to the proportion of infected persons in the population. The former represents a socio-economic system with no policy restrictions on socio-economic activities. The latter, on the other hand, represents a system where there are policy restrictions on socio-economic activities in the form of lockdowns and travel restrictions. If different sub-communities within a society are placed under quarantine with no interaction between these sub-communities, then even if there is an increase in the proportion of infected persons within one sub-community, the likelihood of new interactions (with persons in other sub-communities or even in one sub-community) leading to new infections will be reduced. We represent this with the negative sign of the partial derivative, \(\partial g / \partial i\). Further, we generalize the inequality condition placed earlier on g(0, 0) by removing the restrictions on its sign.
3.2 Equilibria and local stability
Next, we consider the dynamical system represented by (1) and (4). The modified conditions in (4) immediately leads us to modify lemma 1 in page 7 as follows:
Lemma 4
\(g \left( y,i \right) =0\) as defined in (4) is upward-sloping; further, it intersects the y-axis at \({\hat{y}}\) when \(g(0,0)<0\), but intersects the i-axis at \({\bar{i}}_4\) when \(g(0,0)>0\); \( {\hat{y}}, {\bar{i}}_4 \in \mathfrak {R}_{+}\).
Proof
First, we note from (4) that \(\partial g / \partial y >0\) and \(\partial g / \partial i<0\), so it follows that along the curve \(g(y,i) = 0\), we have \(di/dy|_{g (y,i) =0} = - (\partial g / \partial y) / (\partial g / \partial i) >0\), which also provides us with the slope of \(g(y,i)=0 \); i.e. \(g (y,i)= 0\) is upward-sloping. Further, given that \(\partial g / \partial y >0\), for \(g (0,0) <0\), from continuous differentiability of g it follows that \(\exists \ {\hat{y}} \in \mathfrak {R}_{+} \ni g ({\hat{y}}, 0) = 0\), i.e. \(g(y,i)= 0 \) intersects y-axis at \({\hat{y}}\) in the non-negative quadrant. Similarly, given that \(\partial g / \partial i <0\), for \(g (0,0) >0\), from continuous differentiability of g it follows that \(\exists \ {\bar{i}}_4 \in \mathfrak {R}_{+} \ni g ({\hat{y}}, 0) = 0\), i.e. \(g(y,i)= 0 \) intersects i-axis at \({\bar{i}}_4\) in the non-negative quadrant. \(\square \)
Corollary 3.1
For the dynamical system represented by (1) and (4), \(E_1\) and \(E_2\) will always exist in the non-negative quadrant.
Corollary 3.2
Further, if \(g(0,0) >0\), \(E_4\) will also exist in non-negative quadrant.
Proof
Both Corollary 3.1 and 3.2 follows from lemma 4. \(\square \)
Next, we note that with the replacement of the differential Eqs. (2) with (4), we must also modify Lemma 2 and 3 as follows:
Lemma 5
\(( {\hat{y}} - {\bar{y}}_2 ) ( {\hat{i}} - {\bar{i}}_4 ) <0\) is a sufficient condition for \(E_3 \in \mathfrak {R}_{+} \times \mathfrak {R}_{+}\).
Proof
We prove this for two separate cases. First, consider when \(g (0,0) <0\). In this case, we have already shown from lemma 4 that \(\exists \ {\hat{y}} \in \mathfrak {R}_{+} \ni g ({\hat{y}}, 0) = 0\), i.e. \(g(y,i)= 0 \) intersects y-axis at \({\hat{y}}\) in the non-negative quadrant. Further, \(\partial g / \partial i<0 \ \Rightarrow \exists \ {\bar{i}}_4 \le 0 \) such that \( {\bar{i}}_4 \notin \mathfrak {R}_{+} \times \mathfrak {R}_{+} \ \& \ g(0, {\bar{i}}_4) = 0\). If \({\hat{y}} < {\bar{y}}_2\), since \(f({\bar{y}}_2,0) = 0\), from \(\partial f / \partial y<0\) it follows that \(f({\hat{y}},0)>0\). Hence, from the signs of the partial derivatives \(\partial f / \partial y, \partial f / \partial i, \partial g / \partial y, \partial g / \partial i\) it follows that \(\exists \ {\bar{y}}_3 \in [{\hat{y}}, {\bar{y}}_2]\) and \({\bar{i}}_3 \in [0, {\hat{i}}]\) such that \(f ({\bar{y}}_3, {\bar{i}}_3) = 0 = g ({\bar{y}}_3, \bar{i}_3)\). In other words, \(({\bar{y}}_3, {\bar{i}}_3) \in \mathfrak {R}_{+} \times \mathfrak {R}_{+}\) is the interior non-trivial equilibrium, \(E_3\), with \( 0< {\hat{y}} < {\bar{y}}_2\) and \( {\hat{i}}> 0 > {\bar{i}}_4\). Next, we can similarly show for \(g(0,0)>0\), \({\bar{y}}_2>0> {\hat{y}}\) and \({\hat{i}}> {\bar{i}}_4 >0\) is a sufficient condition for the non-trivial equilibrium to exist inside positive orthant. Hence, \(( {\hat{y}} - {\bar{y}}_2 ) ( {\hat{i}} - {\bar{i}}_4 ) <0\) is a sufficient condition for \(E_3 \in \mathfrak {R}_{+} \times \mathfrak {R}_{+}\). \(\square \)
Lemma 6
For the dynamical system represented by (1) and (4):
-
(a)
The Trivial Equilibrium, \(E_1\) is either saddle-point or locally unstable;
-
(b)
The ‘Good Health Equilibrium’, \(E_2\) is saddle-point when \(E_3\) exists in positive orthant and is locally stable otherwise;
-
(c)
The non-trivial equilibrium, \(E_3\) is always locally stable whenever it exists in real positive orthant; and
-
(d)
The ‘Bad Equilibrium’, \(E_4\) is saddle-point.
Proof
Let \(J_1\), \(J_2\), \(J_3\) and \(J_4\) be the jacobian of the dynamical system represented by (1) and (4) evaluated at \(E_1\), \(E_2\), \(E_3\) and \(E_4\) respectively. Next, we note the following:
-
(a)
It would be clear that \(g(0,0)< 0 \ \Leftrightarrow \ \det (J_1) < 0\), i.e. \(E_1\) is saddle point; on the other hand, \(g(0,0) \ge 0 \ \Leftrightarrow \ \det (J_1) >0\) and \(\text {trace}(J_1) >0\), i.e. \(E_1\) is unstable.
-
(b)
Next, with regard to \(E_2\), \(\det (J_2) = \alpha \beta (\partial f / \partial y) g ({\bar{y}}_2, 0 ) {\bar{y}}_2\). We know that \(\partial f / \partial y >0\) from (1); further, if \( {\bar{y}}_2> {\hat{y}}> 0 \Rightarrow g ({\bar{y}}_2, 0) > 0 \ \Rightarrow \det (J_2) <0 \), i.e. \(E_2\) is a saddle-point. On the other hand, \({\bar{y}}_2 \le {\hat{y}} \ \Rightarrow g ({\bar{y}}_2, 0) \le 0 \ \Rightarrow \det (J_2) \ge 0\), and \(\text {trace} (J_2) = \alpha (\partial f / \partial y) \bar{y}_2 + \beta g ({\bar{y}}_2 , 0 ) <0\), i.e. \(E_2\) is locally stable.
-
(c)
Next, we turn to \(E_3\), and note that whenever \(E_3 \in {\mathop {{\mathrm{int}}}} \mathfrak {R}^2 _{++} \), we have, from the signs of partial derivatives in (1) and (4), \( \det (J_3) = \alpha \beta \left( \frac{\partial f}{\partial y} \frac{\partial g}{\partial i} - \frac{\partial f}{\partial i} \frac{\partial g}{\partial y} \right) {\bar{y}}_3 {\bar{i}}_3 > 0\) and \( \text {trace} (J_3) = \alpha (\partial f / \partial y) {\bar{y}}_3 + \beta (\partial g / \partial i) {\bar{i}}_3 <0\). Hence \(E_3\) is locally stable whenever it exists in real positive orthant.
-
(d)
Next, we consider \(E_4\). For \(0< {\bar{i}}_4 < {\hat{i}} \Leftrightarrow f \left( 0, {\bar{i}}_4 \right) > 0\), we have \(\det (J_4) = \alpha \beta (\partial g / \partial i) {\bar{i}}_4 f \left( 0, {\bar{i}}_4 \right) <0\), i.e. \(E_4\) is saddle-point. On the other hand, for \({\bar{i}}_4> {\hat{i}} >0 \Leftrightarrow f \left( 0, {\bar{i}}_4 \right) <0\), we have \(\det (J_4) <0\) & \(\text {trace} (J_4) = \alpha f \left( 0, {\bar{i}}_4 \right) + \beta (\partial g / \partial i) {\bar{i}}_4 <0\), i.e. \(E_4\) is locally stable.
\(\square \)
3.3 Global stability
Next, we turn to the global stability properties of the dynamical system represented by (1) and (4). For any \((y^\circ , i^\circ )\) as the initial point, let \(\Theta \left( t \right) \equiv (y\left( t \right) , i\left( t \right) ; y^\circ , i^\circ )\) be the solution to (1) and (4). We attempt to find out the behavior of this solution as \(t \rightarrow \infty \). We first note the following:
Lemma 7
\( (y^\circ , i^\circ ) \in \left\{ (y,i): y \in [0, {\bar{y}}_2], i=0 \right\} \Leftrightarrow \dot{y} \ge 0 \& \dot{i} = 0\), whereas \( (y^\circ , i^\circ ) \in \{ (y,i): y \in [{\bar{y}}_2, \infty ), i=0 \} \Leftrightarrow \dot{y} \le 0 \& \dot{i} = 0\).
Proof
First we note that since \(E_1: (0,0)\) is a steady state, \((y^\circ , i^\circ ) = (0,0) \Leftrightarrow \dot{y} = 0\). Similarly, \(E_2: (\bar{y}_2, 0)\) is a steady state, so it follows that \((y^\circ , i^\circ ) = ({\bar{y}}_2, 0) \Leftrightarrow f(y,i) = 0 \Leftrightarrow \dot{y} = 0\). Next, we recall from (1) that \(\partial f / \partial y <0\) and \(f({\bar{y}}_2, 0) = 0\), so it follows that \(f(y,0) \ge 0 \ \forall \ y \le {\bar{y}}_2\) and \(f(y,0) \le 0 \ \forall \ y \ge {\bar{y}}_2\). Further, from (4), \(i = 0 \Leftrightarrow \dot{i} = 0\). This completes the proof. \(\square \)
Lemma 8
\( (y^\circ , i^\circ ) \in \{ (y,i): y = 0, i \in [ \max [0, {\bar{i}}_4], \infty ) \} \Leftrightarrow \dot{y} = 0 \ \& \ \dot{i} \le 0\). Further, if \({\bar{i}}_4 >0\), then it follows that \( (y^\circ , i^\circ ) \in \left\{ (y,i): y = 0, i \in (0, {\bar{i}}_4 ) \right\} \Leftrightarrow \dot{y} = 0 \ \& \ \dot{i} \ge 0\).
Proof
First, we note that since \(E_1: (0,0)\) is a steady state, \((y^\circ , i^\circ ) = (0,0) \Leftrightarrow \dot{i} = 0\). Similarly, if \(\bar{i}_4 >0\), then it follows that \(E_4: (0, {\bar{i}}_4) \in \mathfrak {R}_{+} \times \mathfrak {R}_{+}\) is a steady state, so it follows that \((y^\circ , i^\circ ) = (0, {\bar{i}}_4) \Leftrightarrow g(y,i) = 0 \Leftrightarrow \dot{i} = 0\). Next, we recall from (4) that \(\partial g / \partial i <0\) and \(g(0, {\bar{i}}_4) = 0\), so it follows that \(g(0,i) \ge 0 \ \forall \ i \le {\bar{i}}_4\) and \(g(0, {\bar{i}}_4) \le 0 \ \forall \ i \ge {\bar{i}}_4\). Further, from (1), \(y = 0 \Leftrightarrow \dot{y} = 0\). This completes the proof. \(\square \)
We should note that from lemma 7 and 8 , the y and the i axes both are trajectories. Next, we note the following:
Lemma 9
\(f (y,i) \le 0 \ \forall \ \{ (y,i) : y \in \left[ {\bar{y}}_2 , \infty \right) , \ i \in \mathfrak {R}_+ \} \).
Proof
We note that \(f ( {\bar{y}}_2 , i) =0\); further, from (1), we have \(\partial f / \partial y <0 \ \forall \ y \in \mathfrak {R}_+\), so it follows that
Moreover, from (1) we also have \(\partial f / \partial i <0 \ \forall \ i \in \mathfrak {R}_+\). This, along with (5) leads us to the following:
This completes the proof. \(\square \)
Lemma 10
For any \({\tilde{y}} : {\tilde{y}} \in \left[ \max \left[ 0, {\hat{y}} \right] , \infty \right) \), \( \exists \ {\tilde{i}} = i({\tilde{y}}) : g({\tilde{y}}, i) \le 0 \ \forall \ i \in \left[ {\tilde{i}}, \infty \right) \).
Proof
We recall that \(g({\hat{y}}, 0) = 0\). Further from lemma 4, \(g(y,i) =0\) is upward-sloping \(\forall \ (y,i) \in \mathfrak {R}_{+} \times \mathfrak {R}_{+}\). Hence, choosing any arbitrary \({\tilde{y}} : {\tilde{y}} \in \left[ \max \left[ 0, {\hat{y}} \right] , \infty \right) \), we can solve for \(g(y,i)=0\) to yield \({\tilde{i}} = i({\tilde{y}})\) such that \(g({\tilde{y}}, {\tilde{i}}) = 0\). Hence, from (4), we have \(\partial g / \partial y>0\) and \(\partial g / \partial i <0\) so that \(g({\tilde{y}}, i) \le 0 \ \forall \ i \in \left[ {\tilde{i}}, \infty \right) \). This holds true \(\forall \ y \in \left[ \max \left[ 0, {\hat{y}} \right] , \infty \right) \). \(\square \)
Next, we consider \(i \left( {\bar{y}}_2 \right) \) such that \(g \left( {\bar{y}}_2 , i \left( {\bar{y}}_2 \right) \right) = 0\) and \(y ( {\hat{i}} )\) such that \(g ( y ( {\hat{i}} ), {\hat{i}} ) = 0 \).Footnote 3 We define
and
Now, consider the rectangle Q made up of the points: \((0,0), (y^\star , 0), (y^\star , i^\star ), (0, i^\star ) \). This is shown under three possible cases in Fig. 3. Next, we note the following.
Lemma 11
The set \(Q : \{ (y,i): y \in [0, y^\star ], i \in [0, i^\star ] \}\) is invariant for solution to (1) and (4).
Proof
We first note that Q is a rectangular region made up of the area enclosed by the points (0, 0), \((y^\star , 0)\), \((y^\star , i^\star )\) and \((0,i^\star )\). We begin by considering the boundary of the region, \(Q_B \subseteq Q\), where
Note that \(E_1:(0,0)\) and \(E_2:({\bar{y}}_2,0)\) are equilibria which lie on \(Q_B\); further, if \({\bar{i}}_4 \in \mathfrak {R}_{+}\), \(E_4:(0, \bar{i}_4)\) also lies on \(Q_B\). Hence, if the initial point is one of these three points, the solution stays there. Further, from lemma 7 and 8 , any solution with the initial point on either y or i axis but not on one of the equilibria approaches along the axes to one of these equilibria. So these solutions remain in the boundary. Finally, we note that
In other words, if the initial point is on one of the remaining sections of the boundary \(Q_B\), then the solution gets pushed inside the set Q (see Fig. 3). In other words, any solution with initial point on the boundary \(Q_B\) either remains in the boundary or enters Q. Since \(Q \subseteq \mathfrak {R}_{+} \times \mathfrak {R}_{+}\), i.e. is in a plane, any solution starting from inside Q cannot escape Q without crossing \(Q_B\). Thus, the set Q is invariant. \(\square \)
Lemma 12
For any \((y^\circ , i^\circ ) \in \mathfrak {R}_{+} \times \mathfrak {R}_{+}\), the solution \(\Theta \left( t \right) \) must enter Q and either approaches a steady state or is a limit cycle around a steady state in Q.
Proof
First, recall that the axes are trajectories, so for any initial point on the axes, the solution will move along the axes to either \(E_1\), or \(E_2\) or \(E_3\) (if it exists). Next, consider \((y^\circ , i^\circ ) \in \mathop \mathrm{int} Q\). From lemma 11, Q is invariant, so all such solutions remain inside Q. Finally, for \((y^\circ , i^\circ ) \in \left( \mathfrak {R}_{+} \times \mathfrak {R}_{+} \setminus Q \right) \), by construction the solution will eventually hit \(Q_B\) and enter Q. Once a solution enters Q, by Poincaré-Bendixson TheoremFootnote 4 it either approaches one of the equilibria or is a limit cycle around it. \(\square \)
Theorem 1 For the dynamical system represented by (1) and (4), there exists no cyclical or periodic trajectory in \(\mathfrak {R}_{+} \times \mathfrak {R}_{+}\). All trajectories with initial point in \(\mathfrak {R}_{+} \times \mathfrak {R}_{+}\) converges to one of the equilibria.
Proof
Consider the following function:
Next, note that \(\theta (y,i)\) is continuously differentiable in \(\mathfrak {R}_{+} \times \mathfrak {R}_{+} \), and hence in the invariant set, Q. Further,
The expression in (13) has the same sign throughout the connected region Q and hence, satisfies all the criteria for Dulac function, and satisfies Dulac’s criterion for the dynamical system represented by (1) and (4).Footnote 5 Therefore, from Dulac’s criterion, there exists no cyclical or periodic trajectory in \(\mathfrak {R}_{+} \times \mathfrak {R}_{+}\). All trajectories with initial point in \(\mathfrak {R}_{+} \times \mathfrak {R}_{+}\) converges to one of the equilibria. \(\square \)
This result may be stated informally as follows: an effective lockdown strategy involving restrictions on travel and economic activities will rule out the possibilities of waves or cyclical recurrence of infections. We should add, albeit cautiously (given that the simplicity of our model might have come at the cost of ignoring several complexities), that the relative success experienced by China in avoiding waves of infection following a strict lockdown (as seen in Fig. 2) might be an empirical confirmation of our argument above.
4 An example
Let us construct an example to illustrate the results discussed in Sects. 2 and 3 . Consider a dynamical system consisting of linear versions of f(y, i) and g(y, i) as follows:
First, let us consider the onset of pandemic, where the asymptomatic as well as the mildly symptomatic infected individuals continue to have new economic and non-economic interactions with uninfected (susceptible) population, so that the rate of growth of infected proportion of population is a direct function of the existing proportion of infected persons. Let the parameter values be as follows:Footnote 6\( \psi = 1; \eta = 1.2; \kappa = 10; \beta = 1; \theta = 1.5; \gamma = 1.3; \phi = 1 \). The equilibria will then be at \(E_1: (0,0)\), \(E_2: (0.8333, 0)\), \(E_3: (0.6473, 0.0223)\) and \(E_4: (0, 0.7692)\). Starting from an initial point of (0.8, 0.1), we find that the solution converges to the non-trivial equilibrium as long as \(\alpha > {\hat{\alpha }}\), where \({\hat{\alpha }} = 0.03735632183908\) (see Fig. 4).Footnote 7 However, at \(\alpha = {\hat{\alpha }}\) we find that \(E_3\) undergoes a non-degenerate Andronov-Hopf bifurcation and the solution starting from the same initial point, (0.8, 0.1), is a limit cycle around the interior non-trivial steady state, \(E_3\) (see Fig. 5). For \(\alpha < {\hat{\alpha }}\), the solution starting from the same initial point, (0.8, 0.1), explodes and does not converge to any attracting set (see Fig. 6).
Next, we repeat the exercise with \(\partial g / \partial i<0\). This is the case discussed in Sect. 3, with the imposition of restriction on travel and economic activities so that the infected persons do not keep having new interactions. We model this by changing the parameter values in (14), with \(\gamma = -1.3\). We note that as long as \(\theta > \eta \) (i.e. economic activities have a stronger feedback effect on the spread of pandemic by creating newer interactions than the dampening effect on itself due to its own adjustment), the solution converges to the non-trivial steady state, \(E_3\), which lies in the interior of the positive orthant (see Fig. 7). However, for a weaker feedback effect of the economic activities on the spread of pandemic, so that \(\theta < \eta \), the solution converges to the ‘Good Health Equilibrium’, \(E_2\), which signifies an end to the pandemic (see Fig. 8).
Finally, we point out that policy inconsistencies might result in regime shifts from one outcome to another. Consider, for instance, a country which has managed to control the pandemic with lockdowns and restrictions. We now subject this country to a one-time shock, say, from a single super-spreader event. We first examine the effect of this one-time shock without lifting the lockdown and restrictions on travel and economic activities (see Fig. 9a). We then repeat this exercise by again subjecting this economy to a one-time shock at \(t=1000\), this time also simultaneously lifting the lockdown and restrictions on travel and economic activities (see Fig. 9b). We find that if the one-time shock takes place in a regime of continued lockdowns and restrictions, the solution quickly returns to the long-run equilibrium, i.e. the pandemic remains under control. However, in case the one-time shock takes place along with a relaxation of lockdown and restrictions, the solution quickly turns explosive and the pandemic gets out of control.
The important point to note from the above example is the absence of cyclical possibilities when \(\partial g / \partial i <0\). In other words, if non-pharmaceutical interventions are successful in preventing new interactions, then waves of the pandemic can be avoided. Further, non-pharmaceutical interventions can also reduce the value of \(\theta \) with effective implementation of COVID protocols like use of double masks, sanitizers, physical distancing in the society etc. If \(\theta \) can be brought down sufficiently, then even the ‘Good Health Equilibrium’ might be achieved, leading to an end to the pandemic. However, even if the pandemic is brought under control within a country, as long as it continues globally in other parts of the world, a relaxation of lockdown and restrictions might again bring back the waves of infection even from a one-time shock of a single super-spreader event. We might recall, as an example, the case of India demonstrated in Fig. 1d. The Indian Minister for Health declared in early March 2021 that India was in the “endgame” of the epidemic, with many restrictions being lifted over several months. Following a series of super-spreader events like a major religious festival and huge political rallies conspicuous by lack of COVID protocols, the pandemic returned with one of the most severe waves in the world [35].
We would emphasize that, though the simulation exercise in the current Sect. 4 assumes a linear formulation of f and g as well as specific arbitrarily chosen parameter values, the broad conclusion of absence of cycles under non-pharmaceutical interventions is a general result which does not depend on these specifications.
5 Conclusions
In the previous sections, set out a general two dimensional model of interactive dynamics of economic activity and COVID-19. We were able to establish that there were four types of equilibria namely the trivial, the ‘good health’, the non-trivial and the ‘bad’. Depending on the public health policies that are followed (which in turn are partly dependent on the socio-economic-political regime in the country under question), one or the other types of equilibria may be attained in different countries. Without loss of generality it may be asserted that most countries are either converging towards the ‘Good Health’ or the non-trivial equilibria, or cycling around the non-trivial one. Even if initially a country is able to attain a Good Health type equilibrium, slips in policy may result in a regression to an equilibrium with worse outcome in terms of the health of its citizens and the economy.
By only employing restrictions on the first partial derivatives of the two processes in the dynamical system, we are able to establish the stability and cyclical possibilities in this set up. The key specification, in this context, involves the sign of the partial derivative relating the rate of growth of the share of infected persons in the population with respect to the share of the infected persons in the population, \(\partial g / \partial i\). In Sect. 2, we showed that when \(\partial g / \partial i>0\) there is the possibility of recurring cyclical waves of infections and economic activity as has been the case in most countries in the world. This is reflective of policies that have not been effective in preventing the spread of infections across different sub communities within a country. On the other hand, in Sect. 3 we show that the case when \(\partial g / \partial i<0\) represents the situation where the policy has been able to successfully prevent the transmission of infections across the various sub communities in a country with effective restrictions on travel and economic activities. In this case there are no recurrent waves of infection and economic activity but instead, the solution converges to an equilibrium of positive economic activity along with either zero infections (‘Good Health’) or a positive but stable proportion of infected persons. In the former case, the situation tends to approximate what was the case before the onset of the COVID-19 pandemic.Footnote 8 The broad stylized fact that countries like China, which were able to effectively put in place a set of restrictive measures on travel and economic activities early into the pandemic seem to have fared better at avoiding recurrent waves of infections, whereas countries like Sweden which largely avoided such measures fared much worse seem to confirm our point. However, we hasten to add that this is merely a preliminary observation which would require rigorous empirical analysis for a more robust conclusion. We leave this exercise for future research.
The model that has been set out in this paper may be extended in a number of directions of which we mention only two practically relevant ones below.
-
1.
As mentioned before, vaccinations reduce the share of susceptible in the population (at least for a while). Now a substantial ramping up of vaccinations world wide, other things remaining the same, can result in a convergence in the share of the infected in the population to zero. However this may be thwarted in two ways: firstly, the pace of vaccinations may be slow so that there those who were vaccinated in the early phase will have diminished immunity after a while resulting in the share of the susceptible being persistently nonzero (i.e. the share of infected in the population never converging to zero); secondly, the continuous diffusion of the SARS-CoV-2 virus in the population will give rise to new variants which may be resistant to the existing vaccines. Tackling this will require either the pace of vaccine administration to be more rapid than the rise of new variants or the pace of creation of new vaccines to be more rapid than that of further new variants that may emerge. Since the time required to create new vaccines is clearly bounded from below (due to issues connected to due diligence, medical experiment being necessarily temporally open ended etc.), the containment of the pandemic will require a ramping of the process of administering vaccines along with the employment of non-pharmaceutical interventions where appropriate. An incorporation of the dynamic processes of vaccine administration and the emergence of new variants into the model of this paper and the consequences thereof (including the resources required for this world wide vaccination roll out) could be a useful next step in the research direction initiated by this study.
-
2.
A key feature of the waves of infection is their temporal asymmetry. In other words, the gap between the peak and trough of each wave differs. A mathematical representation of this phenomenon as a two dimensional model is possibly involved. Now the incorporation of the share of the vaccinated among the population through a third differential equation with the two existing differential equations of the model will enable the possibility of chaotic dynamics. The latter could form part of a representation of the temporal asymmetry that waves of infection seem to exhibit.
Zhai et al. [39] present a model that incorporates vaccination into an epidemiological model. This model differs from the one presented in our paper in a number of ways of which we mention only on a few. Firstly, unlike the model of our paper, Zhai et al. [39] deal with four categories in the population namely susceptible, exposed, infected and recovered. Secondly, Zhai et al. [39] incorporate a time delay between exposure to the virus and infection. Thirdly, unlike the proposed extension of the model of our paper, the share of the vaccinated in the model is not endogenously modelled by its own differential equation but as a control. While the first two points constitute an advance by and large over the model of our paper, the third point is less so since the assumption that vaccination is a control assumes that there are no constraints on the vaccination process. We contend that vaccination is better dealt with as another differential equation, which might also bring in richer dynamical possibilities, including temporal asymmetry between the peak and the trough across different waves (for instance, in the form of complex chaotic dynamics). We plan to take it up in future extension of this study.
Data Availability Statement
Dataset generated during the simulation exercise, along with the MATLAB code are available from the corresponding author on request. Some points were illustrated using data available in the public domain at World Health Organization COVID-19 Dashboard (https://worldhealthorg.shinyapps.io/covid/).
Notes
This policy conundrum might result from a conflict between multiple policy objectives, and indicative of the socio-economic-political regime within which the policy is conducted. Hence, it might not be necessarily replicated in all countries [24, 25]. However a consideration of these issues is outside the scope of the current study.
Cooper, Mondal, and Antonopoulos [6], for instance, discussed this mechanism in the context of a SIR model. When different localized communities interact each other during periods of surge, the number of susceptible persons might actually increase with an increase in proportion of infected persons during periods of surge in the pandemic as the newly infected persons meet new persons from outside their communities. This was the case in our model in section 2, where the growth in infection, which depend on \(S \times I\) (where S and I are the total number of susceptible and infected persons respectively) rise with rise in I leading to a positive value of the partial derivative, \(\partial g / \partial i\). With lockdowns and travel restrictions, on the other hand, increase in I will be accompanied with fall in S, leading to negative value of \(\partial g / \partial i\).
We note that \({\bar{y}}_2 \gtreqless {\hat{y}} \Leftrightarrow i ({\bar{y}}_2) \gtreqless 0\) and \( {\hat{i}} \gtreqless {\bar{i}}_4 \Leftrightarrow y ({\hat{i}}) \gtreqless 0\).
Poincaré-Bendixson Theorem. A non-empty compact \(\omega \)-limit or \(\alpha \)-limit set of a planar flow, which contains no fixed point, is a closed orbit. [17], page 248-9]
Dulac’s Criterion. If there exists a \(C^1\) function \(\theta (x,y)\) such that the expression \(\frac{\partial (\theta \psi _1)}{\partial x} + \frac{\partial (\theta \psi _2)}{\partial y}\) has the same sign and is not identically zero almost everywhere in a simple connected region of the plane, than the plane autonomous system \(\dot{x} = \psi _1(x,y), \dot{y} = \psi _2(x,y)\) has no non-constant periodic solutions lying entirely within the region. (Originally established by Bendixson [3], later on further refined by Dulac [9], an application of this criterion on a similar system might be found in Mukherji [26], which uses a similar Dulac function as ours.)
We should point out here that the choice of the parameter values in the current simulation exercise is solely for the purpose of illustration of theoretical results in the previous sections. We do not attempt to calibrate either the functional forms or the parameter values with real life data. Since the objective of the current study is to present certain theoretical considerations in a generalized model, such a calibration exercise would be beyond the scope of the current study. We reserve this exercise for future research.
All numerical analyses in this study are performed using Matlab version R2018a (9.4.0.813654).
This will be the case unless economic changes in the interregnum (when the country in question had successfully encountered the pandemic) result in persistent changes in the economy itself. A theoretical discussion of such a case is provided in [31].
References
Anirudh, A.: Mathematical modeling and the transmission dynamics in predicting the Covid-19 - What next in combating the pandemic. Infect. Dis. Model. 5, 366–374 (2020)
Badr Hamada S., et al.: Association between mobility patterns and COVID- 19 transmission in the USA: a mathematical modelling study. In: The Lancet Infectious Diseases (2020)
Bendixson, I.: Sur les courbes définies par des équations différentielles. Acta Math. 24, 1–88 (1901)
Boucekkine R et al.: “The economics of epidemics and contagious diseases: an introduction”. Journal of Mathematical Economics 93. The economics of epidemics and emerging diseases, p. 102498 (2021)
Claeson, M., Hanson, S.: The Swedish COVID-19 strategy revisited. Lancet 397(10285), 1619 (2021)
Cooper, I., Mondal, A., Antonopoulos, C.G.: A SIR model assumption for the spread of COVID-19 in different communities. Chaos Solitons Fractals 139, 110057 (2020)
Crossley, G., Williams, A.: “Wuhan lockdown ‘unprecedented’, shows commitment to contain virus: WHO representative in China”. In: Reuters January 23, 2020 (2020)
Dagpunar, J.S.: Sensitivity of UK Covid-19 deaths to the timing of suppression measures and their relaxation. Infect. Dis. Model. 5, 525–535 (2020)
Dulac, H.: Recherche des cycles limites. CR Acad. Sci. Paris 204, 1703–1706 (1937)
Eichenbaum, M.S., Rebelo, S., Trabandt, M.: Epidemics in the neoclassical and New Keynesian models. Working Paper 27430. National Bureau of Economic Research, (2020)
Eichenbaum, M.S., Rebelo, S., Trabandt, M.: The macroeconomics of epidemics. Working Paper 26882. National Bureau of Economic Research, (2020)
Eichenbaum, M.S., Rebelo, S., Trabandt, M.: The Macroeconomics of Testing and Quarantining. Working Paper 27104. National Bureau of Economic Research, (2020)
Eichenbaum, M.S., et al.: How do people respond to small probability events with large, negative consequences? Working Paper 27988. National Bureau of Economic Research, (2020)
Farboodi, M., Jarosch, G., Shimer, R.: Internal and external effects of social distancing in a pandemic. Working Paper 27059. National Bureau of Economic Research, (2020)
Giuffrida, A., Tondo, O.: “Leaked coronavirus plan to quarantine 16m sparks chaos in Italy”. In: The Guardian March 8, 2020 (2020)
Goenka, A., Liu, L.: Infectious diseases and economic growth. J. Math. Econ. 50, 34–53 (2014)
Hirsch, Morris W.: Smale, Stephen: Differential Equations, Dynamical Systems, and Linear Algebra. Academic Press Inc, New York (1974)
Ivorra, B., et al.: Mathematical modeling of the spread of the coronavirus disease 2019 (COVID-19) taking into account the undetected infections. The case of China. Commun. Nonlinear Sci. Numer. Simul. 88, 105303 (2020)
Kermack, W.O., McKendrick, A.G.: “A contribution to the math- ematical theory of epidemics”. In: Proceedings of the Royal Society of London. A 115.772, pp. 700-721 (1927)
Kucharski, A.J., et al.: Early dynamics of transmission and control of COVID- 19: a mathematical modelling study. Lancet Infect. Dis. 20(5), 553–558 (2020)
Kumar, S., Choudhury, S.: Migrant workers and human rights: a critical study on India’s covid-19 lockdown policy. Soc. Sci. Humanit. Open 3(1), 100130 (2021)
Leung, K., Wu, J.T.: The gradual release exit strategy after lockdown against COVID-19. Lancet Reg Health West Pac 1 (2020)
Lewis, D.: COVID-19 rarely spreads through surfaces. So why are we still deep cleaning. Nature 590(7844), 26–28 (2021)
Macheda, F.: The structural roots of China’s effectiveness against coronavirus pandemic. Int. Crit. Thought 10(4), 605–634 (2020)
Mellish, T.I., Luzmore, N.J., Shahbaz, A.A.: Why were the UK and USA unprepared for the COVID-19 pandemic? The systemic weaknesses of neoliberalism: a comparison between the UK, USA, Germany, and South Korea. J. Glob. Faultlines 7(1), 9–45 (2020)
Mukherji, A.: The possibility of cyclical behavior in a class of dynamic models. Am. J. Appl. Sci. Special Issue, pp. 27-38 (2005)
Nason, G.P.: COVID-19 cycles and rapidly evaluating lockdown strategies using spectral analysis. Sci. Rep. 10, 1–12 (2020)
Ndaïrou, F., et al.: Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos Solitons Fractals 135, 109846 (2020)
Ngonghala, C.N., et al.: Mathematical assessment of the impact of nonpharmaceutical interventions on curtailing the 2019 novel Coronavirus. Math. Biosci. 325, 108364 (2020)
Parui, P.: A simple macro-model of COVID-19 with special reference to India. Metroecon. n/a.n/a (2021)
Patnaik, P.: Macroeconomics of a lockdown. Econ. Polit. Wkly. 55(38), 10–11 (2020)
Press Trust of India.: We are in the endgame of Covid-19 pandemic in India: Health Minister Harsh Vardhan. In: India Today March 7, 2021 (2021)
Rudan, I.: A cascade of causes that led to the COVID-19 tragedy in Italy and in other European Union countries. J. Glob. Health 10(1), 010335 (2020)
Saratchand, C., Kaur, N.: On hegemonic narratives, and the facts regarding China’s response to COVID-19 pandemic. Int. Crit. Thought 10(4), 575–604 (2020)
The Lancet.: India’s COVID-19 emergency. Lancet 397(10286), 1683 (2021)
Thomas, D.M., et al.: A primer on COVID-19 mathematical models. Obesity 28(8), 1375–1377 (2020)
Tsai, A.C., et al.: Coronavirus disease 2019 (COVID-19) transmission in the United States before versus after relaxation of statewide social distancing measures. Clin. Infect. Dis. ciaa1502 (2020)
Yu, X., Qi, G., Hu, J.: Analysis of second outbreak of COVID-19 after relaxation of control measures in India. Nonlinear Dyn. (2020)
Zhai, S. et al.: Vaccination control of an epidemic model with time delay and its application to COVID-19. Nonlinear Dyn. (2021)
Acknowledgements
We are grateful to the two anonymous reviewers for their comments and suggestions, which have helped improve the paper. Some of the results in this paper were presented in the 2021 Web Conference on Economic Theory and Policy organized by National Institute of Public Finance and Policy (New Delhi, India) on March 30-31, 2021. We are grateful to the participants of this conference for their comments and suggestions. It goes without saying that the usual disclaimer applies.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Datta, S., Saratchand, C. Non-pharmaceutical interventions in a generalized model of interactive dynamics between COVID-19 and the economy. Nonlinear Dyn 105, 2795–2810 (2021). https://doi.org/10.1007/s11071-021-06712-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-021-06712-9