Skip to main content

Advertisement

Springer Nature Link
Log in

Was There a Period of Latent Development of COVID-19 in St. Petersburg? Mathematical Simulation Results and Facts

  • Published:
Mathematical Models and Computer Simulations Aims and scope

Abstract

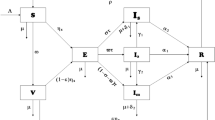
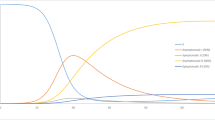
The hypothesis of a latent period of development of the first wave of COVID-19 in St. Petersburg is verified. According to this hypothesis, the appearance of the first patient was preceded by the latent formation of a local variant of the pathogen, caused by the introduction of the pathogen from outside and that occurred asymptomatically in a number of individuals. A mathematical model with two developmental branches, asymptomatic and clinically manifested, is proposed. The possibility of exacerbation of the asymptomatic form or its termination is considered. Other features of the model include accounting for asymptomatic forms, mild and severe forms of the disease, and a decline in the population’s immunity due to the genetic drift of the pathogen. A technique for sequential identification of the considered model in conditions of a shortage of data is proposed. It is demonstrated that verification of the mathematical model requires a sufficiently large number of asymptomatic individuals at the time the first patient was discovered, which is an argument in favor of the validity of the hypothesis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

REFERENCES

  1. A. J. Kucharski, T. W. Russell, C. Diamond, et al., “Early dynamics of transmission and control of COVID-19: a mathematical modelling study,” Lancet Infect. Dis. 20, 553–558 (2020). https://doi.org/10.1016/S1473-3099(20)30144-4

    Article  Google Scholar 

  2. L. Pribylová and V. Hajnova, “SEIAR model with asymptomatic cohort and consequences to efficiency of quarantine government measures in COVID-19 epidemic,” arXiv preprint arXiv:2004.02601 (2020). https://doi.org/10.48550/arXiv.2004.02601

  3. G. Gaeta, “A simple SIR model with a large set of asymptomatic infectives,” Math. Eng. 3 (2), 1–39 (2021). https://doi.org/10.3934/mine.2021013

    Article  MathSciNet  MATH  Google Scholar 

  4. G. Giordano, F. Blanchini, R. Bruno, et al., “Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy,” Nat. Med. 26, 855–860 (2020). https://doi.org/10.1038/s41591-020-0883-7

    Article  Google Scholar 

  5. H.-Y. Cheng, S.-W. Jian, D.-P. Liu, T.-C. Ng, W.-T. Huang, H.-H. Lin, et al., “Contact tracing assessment of COVID-19 transmission dynamics in Taiwan and risk at different exposure periods before and after symptom onset,” JAMA Intern. Med. 180, 1156–1163 (2020). https://doi.org/10.1001/jamainternmed.2020.2020

    Article  Google Scholar 

  6. V. D. Belyakov, D. B. Golubev, G. D. Kaminskii, and V. V. Tets, Self-Regulation of Parasitic Systems: Molecular Genetic Mechanisms (Meditsina, Leningrad, 1987) [in Russian].

    Google Scholar 

  7. I. V. Feldblium, S. O. Golognova, and V. V. Semerikov, “The level and annual dynamics of S. Pneumoniae carriage among different adult population groups,” Epidemiol. Infekts. Bolezni. Aktual. Vopr., No. 5, 13–16 (2015).

  8. S. Felsenstein, J. A. Herbert, P. S. McNamara, and C. M. Hedrich, “COVID-19: Immunology and treatment options,” Clin. Immunol. 215, 108448 (2020). https://doi.org/10.1016/j.clim.2020.108448

    Article  Google Scholar 

  9. P. Sah, M. C. Fitzpatrick, C. F. Zimmer, et al., “Asymptomatic SARS-CoV-2 infection: A systematic review and meta-analysis,” Proc. Natl. Acad. Sci. 118, e2109229118 (2021). https://doi.org/10.1073/pnas.2109229118

    Article  Google Scholar 

  10. M. Alene, L. Yismaw, M. A. Assemie, D. B. Ketema, B. Mengist, B. Kassie, and T. Y. Birhan, “Magnitude of asymptomatic COVID-19 cases throughout the course of infection: A systematic review and meta-analysis,” PloS One 16 (3), e0249090 (2021). https://doi.org/10.1371/journal.pone.0249090

    Article  Google Scholar 

  11. A. B. Zhebrun, S. L. Mukomolov, and O. V. Narvskaya, “Genotyping and molecular labeling of bacteria and viruses in epidemiological surveillance for current infections,” Zh. Mikrobiol. Epidemiol. Immunobiol. 88 (4), 28–36 (2011).

    Google Scholar 

  12. I. D. Kolesin, “Analysis of mechanism of formation of epidemic variant of disease activator,” Biophysics 59, 511–513 (2014). https://doi.org/10.1134/S0006350914030130

    Article  Google Scholar 

  13. K. O. Mironov, A. E. Platonov, M. K. Nikolaev, et al., “Genetic characteristic of Haemophilus influenzae serotype B strains isolated in Russian regions,” Zh. Mikrobiol. Epidemiol. Immunobiol. 87 (1), 24–28 (2010).

    Google Scholar 

  14. A. Yu. Popova, E. B. Ezhlova, A. A. Melnikova, et al., “Distribution of SARS-CoV-2 seroprevalence among residents of the Tyumen region during the epidemic COVID-19 period,” J. Mikrobiol. Epidemiol. Immunobiol. 97, 392–400 (2020). https://doi.org/10.36233/0372-9311-2020-97-5-1

    Article  Google Scholar 

  15. B. F. Maier and D. Brockmann, “Effective containment explains subexponential growth in recent confirmed COVID-19 cases in China,” Science 368, 742–746 (2020). https://doi.org/10.1126/science.abb4557

    Article  MathSciNet  MATH  Google Scholar 

  16. J. L. Gevertz, J. M. Greene, C. H. Sanchez-Tapia, and E.D. Sontag, “A novel COVID-19 epidemiological model with explicit susceptible and asymptomatic isolation compartments reveals unexpected consequences of timing social distancing,” J. Theor. Biol. 510, 110539 (2021). https://doi.org/10.1016/j.jtbi.2020.110539

    Article  MathSciNet  Google Scholar 

  17. S. E. Eikenberry, M. Mancuso, E. Iboi, T. Phan, K. Eikenberry, Y. Kuang, et al., “To mask or not to mask: Modeling the potential for face mask use by the general public to curtail the COVID-19 pandemic,” Infect. Dis. Modell. 5, 293–308 (2020). https://doi.org/10.1016/j.idm.2020.04.001

    Article  Google Scholar 

  18. A. Yu. Popova, E. B. Ezhlova, A. A. Mel’nikova, et al., “Herd immunity to SARS-CoV-2 among the population in Saint-Petersburg during the COVID-19 epidemic,” Probl. Osobo Opasnykh Infekts., No. 3, 124–130 (2020). https://doi.org/10.21055/0370-1069-2020-3-124-130

  19. W. O. Kermack and A. G. McKendrick, “A contribution to the mathematical theory of epidemics,” Proc. R. Soc. London, Ser. A 115, 700–721 (1927). https://doi.org/10.1098/rspa.1927.0118

    Article  MATH  Google Scholar 

  20. World Health Organization. Clinical Management of COVID-19: Interim Guidance, 2020. https://apps.who.int/iris/handle/10665/332196

  21. A. Yu. Popova, E. B. Ezhlova, A. A. Mel’nikova, et al., “Assessment of the herd immunity to SARS-CoV-2 among the population of the Leningrad Region during the COVID-19 epidemic,” Probl. Osobo Opasnykh Infekts., No. 3, 114–123 (2020). https://doi.org/10.21055/0370-1069-2020-3-114-123

  22. Y. Wan, J. Shang, S. Sun, et al., “Molecular mechanism for antibody-dependent enhancement of coronavirus entry,” J. Virol. 94, e02015-19 (2020). https://doi.org/10.1128/JVI.02015-19

    Article  Google Scholar 

  23. R. Anderson and R. May, Human Infectious Diseases. Dynamics and Control (Oxford Univ. Press, Oxford, 1991; Nauchnyi Mir, Moscow, 2004).

  24. W. O. Kermack and A. G. McKendrick, “Contributions to the mathematical theory of epidemics. II.—The problem of endemicity,” Proc. R. Soc. London, Ser. A 138 (834), 55–83 (1932). https://doi.org/10.1098/rspa.1932.0171

    Article  MATH  Google Scholar 

  25. Yu. D. Nechipurenko, A. A. Anashkina, and O. V. Matveeva, “Change of antigenic determinants of SARS-CoV-2 virus S-protein as a possible cause of antibody-dependent enhancement of virus infection and cytokine storm,” Biophysics 65, 703–709 (2020). https://doi.org/10.1134/S0006350920040119

    Article  Google Scholar 

  26. Y. Yi, P. N. P. Lagniton, S. Ye, E. Li, and R-H. Xu, “COVID-19: what has been learned and to be learned about the novel coronavirus disease,” Int. J. Biol. Sci 16, 1753–1766 (2020). https://doi.org/10.7150/ijbs.45134

    Article  Google Scholar 

  27. V. G. Akimkin, S. N. Kuzin, E. N. Kolosovskaya, et al., “Assessment of the COVID-19 epidemiological situation in St. Petersburg,” J. Mikrobiol. Epidemiol. Immunobiol. 98, 497–511 (2021). https://doi.org/10.36233/0372-9311-154

    Article  Google Scholar 

  28. G. Massonis, J. R. Banga, and A. F. Villaverde, “Structural identifiability and observability of compartmental models of the COVID-19 pandemic,” Annu. Rev. Control 51, 441–459 (2021). https://doi.org/10.1016/j.arcontrol.2020.12.001

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. St. Petersburg University, St. Petersburg, Russia

    I. D. Kolesin & E. M. Zhitkova

Authors
  1. I. D. Kolesin
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. E. M. Zhitkova
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding authors

Correspondence to I. D. Kolesin or E. M. Zhitkova.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kolesin, I.D., Zhitkova, E.M. Was There a Period of Latent Development of COVID-19 in St. Petersburg? Mathematical Simulation Results and Facts. Math Models Comput Simul 15, 1037–1044 (2023). https://doi.org/10.1134/S2070048223060133

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S2070048223060133

Keywords: