Stability and optimal control strategies for a novel epidemic model of COVID-19

Abstract

In this paper, a novel two-stage epidemic model with a dynamic control strategy is proposed to describe the spread of Corona Virus Disease 2019 (COVID-19) in China. Combined with local epidemic control policies, an epidemic model with a traceability process is established. We aim to investigate the appropriate control strategies to minimize the control cost and ensure the normal operation of society under the premise of containing the epidemic. This work mainly includes: (i) propose the concept about the first and the second waves of COVID-19, as well as study the case data and regularity of four cities; (ii) derive the existence and stability of the equilibrium, the parameter sensitivity of the model, and the existence of the optimal control strategy; (iii) carry out the numerical simulation associated with the theoretical results and construct a dynamic control strategy and verify its feasibility.

1 Introduction

The global spread of COVID-19 has brought huge disasters to people all over the world. By the end of the December of 2020, there are more than 80,815,542 confirmed cases worldwide, of which approximately 96,397 cases have been confirmed in China [1]. Among them, 1,766,835 people have lost their lives because of this disease. Regrettably, the current spread of the epidemic has not been effectively controlled, and the number of everyday new cases remains high around the world (On December 27, 2020, the number of new cases reached 423,862) [1]. Studying the law of its emergent spread and adopting effective control measures to contain the spread of the epidemic as soon as possible is the problem that people all over the world need to solve urgently.

The study of the novel coronavirus COVID-19 is undoubtedly one of the hottest topics at present. Recently, many scholars have established different infectious disease models to analyze the spread of the epidemic and predict its later development [2, 3]. Wang et al. [4] developed a (susceptible, exposed, infectious, recovered) SEIR model to estimate the epidemic trends in Wuhan. Hellewell et al. [5] established a transmission model and found that efficient contact tracing and case isolation are sufficient to control the new COVID-19 outbreak within 3 months in most cases. Chakraborty et al. [6] have considered a hybrid autoregressive integrated moving average-wavelet-based forecasting (ARIMA-WBF) model to predict various COVID-19 infected countries throughout the world. Some other models have also been established to assess the spread of COVID-19 and emphasize the need for isolation measures [7]. The spread of COVID-19 in different countries can be described by different models. Samui et al. [8] proposed a compartmental mathematical model to predict and control the transmission dynamics of COVID-19 pandemic in India. Zhao et al. [9] developed a SUQC (susceptible, un-quarantined infected, quarantined infected, confirmed infected) model to characterize the dynamics of COVID-19 and explicitly parameterize the intervention effects of control measures in China. Sjödin et al. [10] introduced a compartmental epidemiological model based on the SEIR formulation, and extended it to account for additional variables including compartments for health and intensive care unit (ICU) care. Al-Qaness et al. [11] proposed a new short-term forecasting model using an enhanced version of the adaptive neuro-fuzzy inference system (ANFIS), which has a significantly better chaotic marine predators algorithm (CMPA) than other survey models. Odagaki et al. [12] reformulated a SIQR (susceptible, quarantined, infectious, recovered) model to be appropriate to COVID-19, and the exact properties of the model were presented. Hui et al. [13] established a rumor propagation model and studied the spread mechanism of rumors on social network platform during the spread of COVID-19. In recent years, fractional differential equations have become the focus of research by many scholars, and many meaningful research results have been obtained in theoretical research [14, 15]. Arqub [16] used the reproducing kernel algorithm to solve the time-fractional Schrödinger equations, which provided a new numerical method for solving fractional differential equation. At the same time, nonlinear differential equations enjoying exact solution are of value in the study of theoretical and application problems [17,18,19,20,21,22,23,24]. These theoretical results will promote the application of fractional differential equations in different fields, especially in infectious epidemic modeling. For example, Zhang et al. [25] introduced a fractional-order differential equations model to describe the pattern of transmission of COVID-19 epidemic, and analyzed the dynamics of the model.

In particular, some researchers have proposed various mathematical models to study the optimal control strategies for COVID-19, and have achieved some excellent results. Lemecha et al. [26] proposed a novel COVID-19 epidemic model to obtain the optimal control strategies under the premise of considering the control cost by using the optimal control theory. Khan et al. [27] proposed a COVID-19 epidemic model with a convex incidence rate, and conducted a comprehensive analysis of the dynamic behavior of the model. Afterward, the author established an optimal control problem with the population practicing social distancing and treatment of infected individual as the control item, and got the most effective control strategies by using Pontryagin maximum principle. The total population can be divided into six subpopulations: susceptible, exposed, quarantined, infectious not hospitalized, hospitalized/isolated infectious, and recovered [28]. The author calculated the basic reproductive number of the disease and made a sensitivity analysis to determine the key parameters that affect the spread of the disease. The research work on COVID-19 must be closely related to the measures taken in one country and one region.

The models mentioned above take into account the phenomenon of confirmed patients infecting others. However, patients diagnosed in many countries are strictly isolated and are not transmissible. Under strict isolation measures, patients who are truly communicable during the incubation period. In addition, new coronary pneumonia does not get life-long immunity after the first illness. The model mentioned above does not take into account the re-infection of discharged patients. These will be addressed in this study. For diseases that are infectious during the incubation period, such as COVID-19, it is very important to trace back the people that a confirmed case has been in contact with during the incubation period. This is also the main reason why we frequently see news reports looking for people in the car with patients. Some scholars have started research on epidemic models of contact tracing [29, 30]. Orallo et al. [31] emphasized that the use of a specialized application of smartphone to trace close contacts is a new method of detecting and discovering potentially COVID-19 infected individuals. Their results show that smartphone contact tracing needs to be combined with other control measures (for example, wearing a mask, maintaining social distancing) to be effective. Ferretti et al. [32] believed that the development of a contact-tracing app that can detect and notify the contacts of positive cases in time is an effective means to control the epidemic, without the need for large-scale quarantine. Inspired by these results, in this paper, we included contact tracing from asymptomatic individuals in our general epidemic model framework.

Due to the randomness of population movement and the uncertainty of control measures, the methods to prevent and control the disease are still unclear. Since our government has taken effective measures in a timely manner, the domestic epidemic has been well controlled. By May 2020, the average number of new local infections in China does not exceed 3 cases, and the spread of the disease is basically under control [33]. The second wave of the epidemic has started to rebound in our county since June 2020 due to its complex etiology, strong transmission, and strong environmental seasonal correlation. In this paper, the first wave of the epidemic refers to the period from the first confirmed case to the clearing of COVID-19 patients in Wuhan on April 26, 2020. The re-emergence of newly increased confirmed cases in Beijing on June 11, 2020, indicates that a second wave of the epidemic has started to rebound in China. Subsequently, several domestic cities such as Xinjiang, Liaoning, Qingdao, Tianjin, and Shanghai have experienced small-scale outbreaks.

Table 1 Case data from June 11, 2020, to August 6, 2020, in Beijing

Table 2 Case data from July 22, 2020, to August 29, 2020, in Liaoning

Table 3 Case data from July 17, 2020, to September 7, 2020, in Xinjiang-1 (Urumqi area of Xinjiang)

Table 4 Case data from October 27, 2020, to November 19, 2020, in Xinjiang-2 (Kashgar area of Xinjiang)

Table 5 The meaning of the parameters in the model (1)

In this paper, we will mainly study the spread and control laws of epidemics in the above four places in China during the second wave of epidemics, and establish a scientific mathematical model based on the relevant policies of epidemic control in China. The parameters of the model are determined based on the actual data of the spread of the epidemic in the four groups. The stability analysis, the sensitivity analysis, and the optimal control strategies of the model are further studied. The main goal of this article is to establish a novel epidemic model to describe the spread of COVID-19 in China, and therefore to investigate the appropriate control strategies to minimize the control cost and ensure the normal operation of society under the premise of containing the epidemic. The main contributions of this paper are summarized as follows:

(1):

For the first time, we will divide COVID-19 into two stages, and propose the concepts of the first wave and the second wave. This division helps scholars and disease control departments to study the spread of the epidemic more clearly. We are currently in the second wave of the epidemic and clearly recognizing that there are many objective factors differentiating it from the first wave. This article counts four sets of data from Beijing [34], Liaoning [35], Xinjiang-1 (Urumqi area of Xinjiang) and Xinjiang-2 (Kashgar area of Xinjiang) [36] during the second wave of epidemics, and mines the common characteristics of the four sets of data, which provide a basis for theoretical modeling analysis and parameter selection of numerical simulation.

(2):

We will establish a two-stage susceptible–contacts–susceptible–contacts–infectious–recovered–susceptible (SC-SCIRS) epidemic model. Compared with the traditional infectious epidemic model, it contains two aspects of innovations. One is to consider the traceability investigation at the initial stage of the outbreak, and to check all suspicious people who have a close basis with the case during the incubation period of the virus. The second is to consider that the case will be isolated once it is confirmed, so our model does not consider the case of infected people. It has the ability to spread only during the incubation period, and it provides clear guidance for our later prevention and control, which is also in line with our epidemic prevention and control policy.

(3):

Combined with the current epidemic situation, we will comprehensively consider the cost of disease treatment and control. Considering these two aspects, we will prove the existence of optimal control strategies. In the numerical simulation, we will construct a three-stage dynamic control strategy based on the laws of the data. This strategy is operable and can provide effective suggestions to the disease control department.

The article is organized as follows. In Sect. 2, the data of four cities and their regularity are investigated. In Sect. 3, a novel epidemic model is introduced. The dynamic analysis of the model is completed in Sect. 4. Numerical simulations and a brief summary will be presented in Sects. 5 and 6, respectively.

2 Data mining

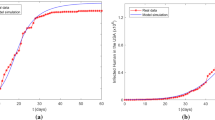
In order to accurately study the law of the incidence and the spread of the second wave of epidemics, we firstly obtain the epidemic case data in Beijing [34], Liaoning [35], and Xinjiang [36] from the official website of the Municipal Health Commission, as shown in Tables 1, 2, 3, and 4, respectively, and the trends of data as shown in (a), (b), (c), and (d) of Fig. 1. Specifically, a total of 335 confirmed cases and a total of 335 discharged cases in Beijing, a total of 93 confirmed cases and a total of 93 discharged in Liaoning, a total of 826 confirmed cases and a total of 826 discharged cases in Xinjiang-1 (Urumqi area of Xinjiang), a total of 78 confirmed cases and a total of 78 discharged cases Xinjiang-2 (Kashgar area of Xinjiang).

From these figures, we can find the following rules:

(1):

The number of new cases reached a peak in about a week, ranging from 14 days to as short as 2 days. There is only one peak of new cases, and there will be a slight rebound in the later period, but the overall trend is declining.

(2):

The largest scale is 826 cases, lasting 54 days, and as few as 78 cases, with a minimum duration of 25 days. That is to say, the epidemic can be completely controlled in less than 2 months.

(3):

No deaths due to illness were reported in the four places, and all confirmed hospitalized cases recovered.

In brief, through the reasonable control of the country, these four epidemics were completely controlled in a relatively short period of time, without large-scale spread and no deaths. The most important thing is that it has not spread to other provinces or other cities, which shows that the control strategy adopted by our country is very efficient. Of course, the cost of control we pay is also huge. The Beijing News reported on June 25, from 98 testing institutions with a daily testing capacity of more than 40,000 copies to 128 institutions, 480 sampling sites, 2422 sampling points, with a daily testing capacity of more than 30,000 copies. In just over 10 days, Beijing has continued to improve its nucleic acid testing capabilities and expand the scope of testing. As of 0:00 on June 22, the city had sampled 2.948 million people from core areas and groups, and the total number of people detected was 2.342 million [37].

In fact, it shows that China’s control strategy for the epidemic is correct and efficient. It is of practical guiding significance to study epidemic control strategies and the law of disease transmission. Based on the official data and prevention and control policies during the second wave of the epidemic in China, we will build an epidemic model suitable for China’s strategy in the next section, aims to study the optimal control strategy that takes both cost and effect into consideration.

Fig. 1

Case data in four cities

3 Mathematical modeling

According to current epidemiological investigations, the average incubation period of COVID-19 is about 7 days, with a minimum of 2–3 days and a maximum of 24 days. General medical observations are based on 14 days. Under the current epidemic prevention and control policies in China, imported overseas cases and domestic cases must be isolated in a very safe way and are not in a position to spread to others. However, confirmed cases are also transmissible during the incubation period, which shows exactly the difficulty in controlling the epidemic. When one or more cases are detected in a city, the first measure that needs to be taken immediately is to trace the contacts closely related to the case, including his colleagues, family members, and the main group of people in the activity track within 14 days. The supermarkets, restaurants, and vehicles he traveled in must be strictly checked. Based on the current advanced information technology and the high popularity of communication equipment, people who have direct and indirect contact with confirmed cases can be quickly identified.

Strictly isolating confirmed cases and focusing on tracing people who have been in contact with confirmed cases are two important measures to control the spread of the epidemic. To more effectively prevent the spread of the outbreak, we have expanded the contact population to include people who are close to the case in the region. For example, a case was confirmed in the Beijing Xinfadi market on June 11, 2020. The people we need to closely control including not only those who have direct or indirect contact with the case within 14 days but also all residents within a certain spatial distance centered on the Xinfadi market. This containment relationship and the evolution of the epidemic are shown in Figs. 2 and 3, where $\tau _{1}$ and $\tau _{2}$ represent two random times, with $\tau _{1}$ representing the time when the first case of the epidemic was confirmed, and $\tau _{2}$ representing the time when the last case of the epidemic was discharged. The variables $S_{1}(t)$ and S(t) represent the class of susceptible in two different periods, and $C_{1}(t)$ represents the class of direct contact with confirmed cases in the previous 14 days. The variable C(t) represents the class of direct or indirect contacts with the case, and C(t) must include and have a wider range than $C_{1}(t)$. In Fig. (2), the rectangular bar, $C_{1}(\tau _{1})$, can be used to indicate the people who have been in contact with all the movement trajectories of the case, then $C(\tau _{1})$ includes direct and indirect contacts and all residents within a certain distance from the source of the disease. The variable C(t) represents the class of confirmed case, and R(t) represents the class of recovered in confirmed case.

Fig. 2

Traceability process of contacts with cases

Fig. 3

Scheme of the SC-SCIR model transmission for COVID-19

Drawing on the modeling theory of epidemic, we establish the following SC-SCIR model according to the evolution relationship in Fig. 3

$$\begin{aligned} \left\{ \begin{aligned}&\text {The first stage: }\\&\left. \begin{aligned}&\dot{S_{1}}(t)=-\beta _{1} S_{1}(t)C_{1}(t)\\&\dot{C_{1}}(t)=\beta _{1} S_{1}(t)C_{1}(t)+\alpha \nu C_{1}(t)\\ \end{aligned}\quad \right\} t \in [-14,\tau _{1}],\\&\text {The second stage:}\\&\left. \begin{aligned}&{\dot{S}}(t)=\Lambda -[\beta -u(t)] \mathrm{SC}-\mu S+\varphi C+\xi R\\&{\dot{C}}(t)=[\beta -u(t)] \mathrm{SC}-(\eta -\varphi ) C\\&{\dot{I}}(t)=\eta C-(\gamma +\varepsilon )I\\&{\dot{R}}(t)=\gamma I-\xi R\\ \end{aligned} \quad \right\} t\in (\tau _{1},\tau _{2}]. \end{aligned} \right. \end{aligned}$$

(1)

The six equations in model (1) describe two different stages of the spread of the epidemic. The first stage mainly describes the number of contacts with the case from the first patient diagnosis to the previous 14 days (the incubation period of the virus), aiming to unearth all direct or indirect contact with the case. The second stage mainly describes the outbreak of the epidemic from the diagnosis of the first patient to the discharge of the last case, aiming to study the spread of the epidemic, and then adopt effective control strategies. The modeling idea of the two-stage model is derived from the spread of the incubation period of COVID-19, which is also the innovation of the model in this article compared with the traditional epidemic model. In addition, considering China’s current strict isolation policy for patients, another innovation of this model is that it does not consider the transmission rate of confirmed cases. In our model (1), the two equations in the first stage are used to describe the traceability process. This process is not an infectious process. The $\alpha$ individuals diagnosed at the moment of $\tau _{1}$ is used as the source to trace back the populations $\alpha \nu C_{1}(t)$ with whom they have direct contact within 14 days, and the indirect basic population $\beta _{1} S_{1}(t)C_{1}(t)$. It is worth emphasizing that the parameters $\beta _{1}$ and $\beta$ in the model (1) are not the infection rate, but the contact rate between people in different periods, and the meaning of other parameters in model (1) are shown in Table 5.

The evolution of the second stage is described by the last four equations of the model. Since the confirmed cases are isolated, our model does not consider the case infection item $\beta \mathrm{SI}$, which is also the biggest difference between our model and the traditional epidemic model. In our model, C(t) indicates people who have direct or indirect contact with the case and are geographically close to the source of the disease. The contact class C(t) may be an infected latent person, that is, the class C(t) may become I(t). Of course, C(t) may not be infected, and after the incubation period, its suspiciousness will be ruled out and become a susceptible. In addition, it is also necessary to consider that COVID-19 does not receive lifelong immunity after a cure. Therefore, the class of recovered R(t) will become a susceptible again. However, after undergoing a treatment, the class of recovered R(t) will become more aware of self-protection compared to ordinary residents.

Based on the above analysis, an effective way to control the spread of the epidemic is to control the contact between C(t) and S(t) in the area after the moment of $\tau _{1}$. Given that the population of C(t) is huge, it is costly to achieve complete isolation of C(t). At the same time, this is unnecessary and will hinder the normal society from resuming work and production order in the region. On the other hand, if the class C(t) is not controlled, it will inevitably lead to serious epidemic spread. Therefore, it is very necessary to choose an appropriate control strategy so that the epidemic can be effectively controlled within a small area, while also ensuring the normal operation of various social tasks. In the next section, we will conduct a comprehensive analysis of the dynamic behavior and optimal control strategy of the model (1).

4 Main results

Note that the model (1) includes the SC model before $\tau _{1}$ and the SCIRS after $\tau _{1}$. The SC model is a tracing process. It is calculated and inferred according to the contact rate between people in $[\tau _{1}-14, \tau _{1}$] all contacts C(t), then which can provide initial value basis for the SCIRS model. Therefore, we only need to analyze the dynamic behavior of the SCIRS model as follows

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{S}}(t)=\Lambda -[\beta -u(t)] SC-\mu S+\varphi C+\xi R,\\&{\dot{C}}(t)=[\beta -u(t)] SC-(\eta +\varphi ) C,\\&{\dot{I}}(t)=\eta C-(\gamma +\varepsilon )I,\\&{\dot{R}}(t)=\gamma I-\xi R,\\&S(\tau _{1})=0,\quad C(\tau _{1})=C_{1}(\tau _{1})+\rho (P),\\&\qquad I(\tau _{1})=0,\quad R(\tau _{1})=0,\\&t\in [\tau _{1},\tau _{2}], \end{aligned}\right. \end{aligned}$$

(2)

where $\rho (P)$ represents all residents within the range of P from the source of disease $\rho$. The first goal of our research is to establish a suitable control strategy u(t) so that all cases are cured and all contacts are released from medical observation $\tau _{2}$, that is

$$\begin{aligned} \lim _{t\rightarrow \tau _{2}}C(t)=\lim _{t\rightarrow \tau _{2}}I(t)=\lim _{t\rightarrow \tau _{2}}R(t)=0 \end{aligned}$$

and $\lim _{t\rightarrow \tau _{2}}S(t)=\chi$, where $\chi$ represents a relatively constant population of the city.

4.1 Stability of disease-free equilibrium

The model (2) is a nonautonomous system, because the contact rate $\beta -u(t)$ depends on the time t. The control function u(t) is very sensitive to time. In the early stage of the epidemic, the intensity of control is greatest. As the epidemic is gradually controlled, it is necessary to reduce the degree of control and gradually restore normal social production order. For the convenience of studying the problem, we define an average contact rate as follows

$$\begin{aligned} {\bar{\beta }}=\frac{\int _{\tau _{1}}^{\tau _{2}}[\beta -u(t)]\,\mathrm {d}t}{\tau _{2}-\tau _{1}}. \end{aligned}$$

(3)

In view of the classic methods of infectious diseases (see [41]), we define the basic reproduction number of the model (2) as follows

$$\begin{aligned} {\mathcal {R}}_{0}=\frac{\Lambda \beta }{\mu \eta +\mu \varphi }. \end{aligned}$$

(4)

Of course, the meaning of ${\mathcal {R}}_{0}$ in this paper is different from the average infection rate in infectious diseases. Here, ${\mathcal {R}}_{0}$ only refers to the average number of susceptible persons in contact with one contact. Through direct calculation, the following lemma can be obtained.

Lemma 1

The model (2) admits a disease-free equilibrium $E_{0}\left( \frac{\Lambda }{\mu },0,0,0\right)$ if the basic reproduction number ${\mathcal {R}}_{0}<1$; if ${\mathcal {R}}_{0}>1$, then the model (2) admits another nontrivial positive equilibrium as follows

$$\begin{aligned}&E_{1}=(S^{*},C^{*},I^{*},R^{*})\\&\quad =\left( \frac{\eta +\varphi }{\beta },\,\frac{(\gamma +\varepsilon )(\Lambda \beta -\mu \eta -\mu \varphi )}{\beta \eta \varepsilon },\,\right. \\&\qquad \left. \frac{\Lambda \beta -\mu \eta -\mu \varphi }{\beta \varepsilon },\,\frac{\gamma (\Lambda \beta -\mu \eta -\mu \varphi )}{\beta \varepsilon \xi }\right) . \end{aligned}$$

We have the following conclusions about the stability of disease-free Theorem $E_{0}$.

Theorem 1

The disease-free equilibrium $E_{0}\left( \frac{\Lambda }{\mu },0,0,0\right)$ of model (1) is globally asymptotically stable if $\frac{{\tilde{\beta }}\Lambda }{\mu }<\eta +\varphi$.

Proof

Letting the right sides of the four equations of the model (2) equal to $f_{1}(S,C,I,R)$, $f_{2}(S,C,I,R)$, $f_{3}(S,C,I,R)$ and $f_{4}(S,C,I,R)$, then we can calculate the Jacobian matrix of the model (2)

$$\begin{aligned}&J|_{(S,C,I,R)}=\begin{pmatrix} \frac{\partial f_{1}}{\partial S}&{}\quad \frac{\partial f_{1}}{\partial C}&{}\quad \frac{\partial f_{1}}{\partial I}&{}\quad \frac{\partial f_{1}}{\partial R}\\ \frac{\partial f_{2}}{\partial S}&{}\quad \frac{\partial f_{2}}{\partial C}&{}\quad \frac{\partial f_{2}}{\partial I}&{}\quad \frac{\partial f_{2}}{\partial R}\\ \frac{\partial f_{3}}{\partial S}&{}\quad \frac{\partial f_{3}}{\partial C}&{}\quad \frac{\partial f_{3}}{\partial I}&{}\quad \frac{\partial f_{3}}{\partial R}\\ \frac{\partial f_{4}}{\partial S}&{}\quad \frac{\partial f_{4}}{\partial C}&{}\quad \frac{\partial f_{4}}{\partial I}&{}\quad \frac{\partial f_{4}}{\partial R}\\ \end{pmatrix}\\&\quad =\begin{pmatrix} -[\beta -u(t)]C-\mu &{} -[\beta -u(t)] S+\varphi &{} 0 &{}\xi \\ [\beta -u(t)]C &{} [\beta -u(t)]S-(\eta +\varphi ) &{} 0 &{} 0\\ 0 &{} \eta &{} -(\gamma +\varepsilon ) &{} 0\\ 0 &{} 0&{} \gamma &{} -\xi \\ \end{pmatrix}. \end{aligned}$$

Further, we get

$$\begin{aligned} \left. J\right| _{\left( \frac{\Lambda }{\mu },0,0,0\right) }=\begin{pmatrix} -\mu &{} -\frac{{\tilde{\beta }}\Lambda }{\mu }+\varphi &{} 0 &{}\xi \\ 0 &{} \frac{{\tilde{\beta }}\Lambda }{\mu }-(\eta +\varphi ) &{} 0 &{} 0\\ 0 &{} \eta &{} -(\gamma +\varepsilon ) &{} 0\\ 0 &{} 0&{} \gamma &{} -\xi \\ \end{pmatrix}. \end{aligned}$$

We can get the characteristic equation of the Jacobian matrix $\left. J\right| _{\left( \frac{\Lambda }{\mu },0,0,0\right) }$

$$\begin{aligned} \begin{aligned}&f(\lambda )=|\lambda E-J|_{\left( \frac{\Lambda }{\mu },0,0,0\right) }\\&\quad =\begin{pmatrix} \lambda +\mu &{} -\frac{{\tilde{\beta }}\Lambda }{\mu }-\varphi &{} 0 &{}-\xi \\ 0 &{} \lambda -\frac{{\tilde{\beta }}\Lambda }{\mu }+(\eta +\varphi ) &{} 0 &{} 0\\ 0 &{} -\eta &{} \lambda +(\gamma +\varepsilon ) &{} 0\\ 0 &{} 0&{} -\gamma &{} \lambda +\xi \\ \end{pmatrix}\\&\quad =(\lambda +\gamma +\varepsilon )(\lambda +\mu )(\lambda +\xi )\left( \lambda +\eta +\varphi -\frac{{\tilde{\beta }}\Lambda }{\mu }\right) =0. \end{aligned} \end{aligned}$$

It is easy to get the four eigenvalues of the characteristic equation

$$\begin{aligned} \lambda _{1}= & {} -(\gamma +\varepsilon ),\quad \lambda _{2}=-\mu ,\quad \lambda _{3}=-\xi ,\quad \\ \lambda _{4}= & {} \frac{{\tilde{\beta }}\Lambda }{\mu }-(\eta +\varphi ). \end{aligned}$$

Obviously, the eigenvalues of the characteristic equation are all negative if $\frac{{\tilde{\beta }}\Lambda }{\mu }<\eta +\varphi$. Therefore, in view of Lyapunov stability theory (see [41]), we can get the conclusion that disease-free equilibrium $E_{0}\left( \frac{\Lambda }{\mu },0,0,0\right)$ of the model (1) is globally asymptotically stable. The proof is completed. $\square$

Remark 1

Stability is relative to the equilibrium, which refers to the ability of the system to continue to maintain equilibrium after being disturbed. For the disease-free equilibrium $E_{0}$ of the model (2), its global asymptotic stability means that the solution of the model (1) will still converge to $E_{0}$. Of course, to ensure the stability of $E_{0}$, the condition ${\mathcal {R}}_{0}<1$ must be satisfied. Therefore, analysis of the sensitivity of each parameter in ${\mathcal {R}}_{0}$ combined with the operability of the parameters is very necessary for more effective control of the epidemic.

The disease-free equilibrium $E_{0}\left( \frac{\Lambda }{\mu },0,0,0\right)$ is the ultimate goal of epidemic control. Note that the stability of disease-free equilibrium is related to the basic reproduction number ${\mathcal {R}}_{0 }$. In order to ensure that the conditions of the theorem are met, its effective measures should reduce the contact rate ${\bar{\beta }}$. According to current official data, the probability that new coronary pneumonia forming an endemic disease is almost zero. Under China’s epidemic policy, even if there is a wavelet epidemic, it still does not have the conditions to form an endemic disease. Therefore, we will not discuss the stability of the positive equilibrium $E_{1}$ of the model (2) when ${\mathcal {R}}_{0}>1$. In this paper, we mainly study the appropriate control strategies to ensure ${\mathcal {R}}_{0}<1$.

4.2 Sensitivity indices of model (2)

According to the conclusions obtained in Sect. 4.1, the basic reproduction number R0 is an important indicator for epidemic control. Therefore, as long as the analysis is clear about the sensitivity of each parameter to R0 and the operability of epidemic control, it reflects how each of the COVID-19 parameters influcence the performance of the proposed approach. First, we analyze the sensitivity of basic reproduction number ${\mathcal {R}}_{0}$ to various parameters. According to the literature [40], we give the following definition.

Definition 1

The normalized forward sensitivity index of a variable ${\mathcal {R}}_{0}$ depends on a parameter p, and is defined as:

$$\begin{aligned} \gamma _{p}^{{\mathcal {R}}_{0}}:=\frac{\partial {\mathcal {R}}_{0}}{\partial p}\times \frac{p}{{\mathcal {R}}_{0}}. \end{aligned}$$

It is easy to calculate that

$$\begin{aligned} \begin{aligned} \gamma _{\Lambda }^{{\mathcal {R}}_{0}}&=\frac{ \beta }{\mu \eta +\mu \varphi }\frac{\mu \eta +\mu \varphi }{\beta }=1,\quad \\ \gamma _{\beta }^{{\mathcal {R}}_{0}}&=\frac{\Lambda }{\mu \eta +\mu \varphi }\frac{\mu \eta +\mu \varphi }{\Lambda }=1,\quad \\ \gamma _{\mu }^{{\mathcal {R}}_{0}}&=-\frac{1}{\mu ^{2}}\frac{\Lambda \beta }{\eta +\varphi } \frac{\mu ^{2}(\eta +\varphi )}{\Lambda \beta }=-1,\\ \gamma _{\eta }^{{\mathcal {R}}_{0}}&=-\frac{1}{(\eta +\varphi )^{2}}\frac{\Lambda \beta }{\mu }\frac{\eta \mu (\eta +\varphi )}{\Lambda \beta }=-\frac{\eta }{\eta +\varphi },\quad \\ \gamma _{\eta }^{{\mathcal {R}}_{0}}&=-\frac{1}{(\eta +\varphi )^{2}}\frac{\Lambda \beta }{\mu }\frac{\varphi \mu (\eta +\varphi )}{\Lambda \beta }=-\frac{\varphi }{\eta +\varphi }. \end{aligned} \end{aligned}$$

According to the basic characteristics of the epidemic model, the smaller the basic reproduction number ${\mathcal {R}}_{0}$ is, the more conducive it is to control the spread of the disease. In the article, ${\mathcal {R}}_{0}$ describes the cumulative scale of the contact population C(t) and the speed at which it tends to zero. Because of the sensitivity analysis of the parameters of ${\mathcal {R}}_{0}$, the input rate $\Lambda$ and the contact rate $\beta$ are positively correlated with ${\mathcal {R}}_{0}$ . That is, it is an effective way to control the epidemic by effectively reducing the imported population and controlling the direct contact of the population in the city. The parameters $\mu$, $\eta$, and $\varphi$ are negatively related to ${\mathcal {R}}_{0}$. In other words, increasing the values of these three parameters is beneficial to controlling the epidemic. At present, all walks of life are operating normally, and residents participate in necessary work and social activities, which means that $\mu$ is small and there must be an upper bound. The parameter $\eta$ is the infection rate of the class contacts, which is determined by the inherent transmission nature of the disease. We do not want to increase the infection rate to achieve the goal of controlling the epidemic. The parameter $\varphi$ means that the contact ruled out the possibility of being infected this time, which requires multiple nucleic acid tests and the incubation period to reach a conclusion.

In short, the above analysis shows that the three parameters negatively correlated with ${\mathcal {R}}_{0}$ are not controllable, or not currently the most effective method. Similarly, for the input entrance $\Lambda$ of a big city, the existence range does not have strong controllability. The most effective way is to control the contact rate, appropriately reduce the necessary social activities, take protective measures in public places, and maintain the necessary safety distances. However, control is costly and will inevitably affect the normal production order of society. The focus of this paper is to calculate the optimal control strategy, which can not only control the spread of the epidemic but also minimize the control cost. In the next section, we will give relevant conclusions.

4.3 Optimal control strategies

Let u(t) be the control variable used to control the contact rate of contacts with other susceptible individuals. We define the set of allowed control functions as $U=\{u(t), 0<u(t)<\beta , t\in [\tau _{1},\tau _{2}]\}$. The main aim is to study the optimal control strategy, considering both the costs of treatment of infected individuals and the costs of control. The objective is to

$$\begin{aligned} \min J[u(t)] =\int _{\tau _{1}}^{\tau _{2}}[\kappa _{1} I^{2}(t)+\kappa _{2}u^{2}(t)]\,\mathrm {d}t, \end{aligned}$$

(5)

where $\kappa _{1}$ and $\kappa _{2}$ represent the weight of control population contact cost and the treatment cost of the infected, respectively. Since all variables in the model are continuous, the solution of the control system is bounded. In addition, the objective function is convex with respect to the control variable u(t). Therefore, in view of Filippove–Cesari theorem (see [38]), we can get the conclusion that the solution to the optimal control problem is existential.

Theorem 2

The control problems (2) and (5) with initial conditions $(S_{1}(\tau _{1}),C(\tau _{1}),\alpha , 0)$ exist a unique optimal solution $(S^{*}(\cdot ),C^{*}(\cdot ),I^{*}(\cdot ),R^{*}(\cdot ))$ associated with an optimal control $u^{*}(t)$ on $[\tau _{1},\tau _{2}]$, with fixed final time $t_{f}$, where

$$\begin{aligned} u^{*}(t)=\min \left\{ \beta ,\,\,\max \left( 0,\,\, \frac{(\lambda _{2}-\lambda _{1})S(t)C(t)}{2\kappa _{2}}\right) \right\} . \end{aligned}$$

Moreover, there exist adjoint functions $\lambda _{i}^{*}(\cdot )$, $i=1,2,3,4$, satisfying

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{\lambda }}_{1}^{*}(t)=(\lambda _{1}-\lambda _{2})[\beta -u(t)]C(t)+\mu \lambda _{1},\\&{\dot{\lambda }}_{2}^{*}(t)=(\lambda _{2}-\lambda _{1})[\beta -u(t)]S(t)\\&\quad +\lambda _{2}(\eta -\varphi )-(\lambda _{1} +\lambda _{3}),\\&{\dot{\lambda }}_{3}^{*}(t)=(\gamma +\varepsilon )\lambda _{3}-\gamma \lambda _{4},\\&{\dot{\lambda }}_{4}^{*}(t)=(\lambda _{4}-\lambda _{1})\xi ,\\ \end{aligned}\right. \end{aligned}$$

and the transversality conditions $\lambda _{i}^{*}=0$, $i=1,2,3,4.$

Proof

According to the Pontryagin maximum principle [39], the Hamiltonian function H of control problems (2) and (5) is defined by

$$\begin{aligned} \begin{aligned}&H(S,C,I,R,\lambda ,u(t))\\&\quad =\kappa _{1}I^{2}(t)+\kappa _{2}u^{2}(t)\\&\qquad +\lambda _{1}(t)(\Lambda -[\beta -u(t)] SC-\mu S+\varphi C+\xi R)\\&\qquad +\lambda _{2}(t)([\beta -u(t)] SC-(\eta -\varphi ) C)\\&\qquad +\lambda _{3}(t)(\eta C-(\gamma +\varepsilon )I) +\lambda _{4}(t)(\gamma I-\xi R), \end{aligned} \end{aligned}$$

where $\lambda (t)=(\lambda _{1}(t),\lambda _{2}(t),\lambda _{3}(t),\lambda _{4}(t))$ with a nontrivial absolutely continuous mapping $\lambda :\,[0,t_{f}]\rightarrow {\mathbb {R}}$, such that

$$\begin{aligned} {\dot{S}}(t)= & {} \frac{\partial H}{\partial \lambda _{1}},\quad {\dot{C}}(t)=\frac{\partial H}{\partial \lambda _{2}},\quad \\ {\dot{I}}(t)= & {} \frac{\partial H}{\partial \lambda _{3}},\quad {\dot{R}}(t)=\frac{\partial H}{\partial \lambda _{4}},\quad \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \lambda _{1}(t)&=-\frac{\partial H}{\partial S}=(\lambda _{1}-\lambda _{2})[\beta -u(t)]C(t)+\mu \lambda _{1}, \\ \lambda _{2}(t)&=-\frac{\partial H}{\partial C}=(\lambda _{2}\\&\quad -\lambda _{1})[\beta -u(t)]S(t)+\lambda _{2}(\eta -\varphi )-(\lambda _{1} +\lambda _{3}),\\ \lambda _{3}(t)&=-\frac{\partial H}{\partial I}=(\gamma +\varepsilon )\lambda _{3}-\gamma \lambda _{4},\\ \lambda _{4}(t)&=-\frac{\partial H}{\partial R}=(\lambda _{4}-\lambda _{1})\xi ,\\ \end{aligned} \end{aligned}$$

and the minimization condition

$$\begin{aligned}&H(S^{*}(t),C^{*}(t),I^{*}(t),R^{*}(t),\lambda ,u^{*}(t))\\&\quad = \min _{0<u(t)\le \beta }H(S^{*}(t),C^{*}(t),I^{*}(t),R^{*}(t),\lambda ,u(t)) \end{aligned}$$

holds almost everywhere on $[\tau _{1},\tau _{2}]$. Moreover, the transversality conditions $\lambda _{i}(t_{f})=0$ hold. The optimal control in the above formula $u^{*}(t)$ can be obtained by the stationary point of the function, let

$$\begin{aligned} \left. \frac{\partial H}{\partial u}\right| _{u(t)=u^{*}(t)}=2\kappa _{2}u^{*}(t)+(\lambda _{1}-\lambda _{2})S(t)C(t)=0, \end{aligned}$$

then we get

$$\begin{aligned} u^{*}(t)=\min \left\{ \beta ,\,\,\max \left( 0,\,\, \frac{(\lambda _{2}-\lambda _{1})S(t)C(t)}{2\kappa _{2}}\right) \right\} . \end{aligned}$$

In summary, the control problem admits a unique optimal solution $(S^{*}(\cdot ),C^{*}(\cdot ),I^{*}(\cdot ),R^{*}(\cdot ))$ associated with an optimal control $u^{*}(t)$ such that the objective function to the minimum. The proof is completed. $\square$

Remark 2

The objective function (5) includes two parts: the number of infected people and the cost of control, which establishes the rules for the optimal control strategy. In other words, we need to take into account the epidemic situation and control costs at the same time as the rules for establishing the optimal control strategy.

The conclusion of Theorem (2) not only gives the existence of optimal control but also gives the expression of optimal control $u^{*}(t)$, which is very important. This means that there is an appropriate scale to control population contact, avoiding the harm caused by two extreme strategies. If the control strategy is too strong, it is true that the best control effect will be achieved, but huge control costs need to be paid, which will affect the normal production order of the society. In addition, based on the current world’s full understanding of the epidemic and China’s abundant medical resources, transitional restrictions on social communication are unnecessary and a waste of resources. At this stage, the complete restoration of normal order without control will inevitably lead to the spread of the epidemic. Therefore, it is very necessary to study the reasonable control intensity.

5 Numerical simulation and discussion

To illustrate and further expand our theoretical results, we use the software MATLAB to perform numerical simulation on the model (2). Because our model mainly studies China’s transmission laws and control strategies during the second wave of epidemics, regarding the selection of parameters in the model (2), we mainly use the data in Tables 1, 2, 3, and 4. For example, in the four sets of data, there are no deaths and all patients recovered. Therefore, we select the death rate $\varepsilon =0$ and the recovery rate $\gamma =1$. Note that the number of confirmed cases in a single day and the overall scale of the epidemic are smaller, which means that the contacts will recover with a very high probability, so we set $\varphi =0.99$ and $\eta =0.01$. The selection of other parameters is also based on actual data, as shown in Table 6.

Table 6 Major parameters of model (2)

Also, in order to highlight the role of contact rate in the spread of the epidemic, first we assume that $u(t)=0$ and $\beta =0.2$. In other words, without a control strategy, a fixed contact rate $\beta$ is given to show the long-term asymptotic dynamic behavior of the model (2). Furthermore, we give four different sets of $\beta$ values to compare the regulation evolution of S(t), C(t), I(t), R(t), respectively. We can calculate the basic regeneration number ${\mathcal {R}}_{0}$ under four groups of different contact rates as follows

$$\begin{aligned}&\left. {\mathcal {R}}_{0}\right| _{\beta =0.8}=0.7339, \quad \left. {\mathcal {R}}_{0}\right| _{\beta =0.6}= 0.5505,\\&\left. {\mathcal {R}}_{0}\right| _{\beta =0.4}=0.3670, \quad \left. {\mathcal {R}}_{0}\right| _{\beta =0.2}=0.1835. \end{aligned}$$

In view of Theorem 1, the solution of the model (2) will converge to the equilibrium disease-free equilibrium $E_{0}$ if ${\mathcal {R}}_{0}<1$. According to the basic theory of epidemic, the smaller the value of the basic reproduction number ${\mathcal {R}}_{0}$ is, the faster the model solution converges to the disease-free equilibrium point is. In (a) of Fig. (4), we can see that the solution of the model (2) converges to the equilibrium point within 50 days to 60 when $\beta =0.2$. With the increase in $\beta$ (from 0.2 to 0.8), the population of contacted C(t), the infected I(t), and the recovered R(t) all increase, and its convergence to 0 will also slow down and will be delayed for about 100 days, which are shown in a, b, and c of Fig. (4). Note that ${\mathcal {R}}_{0}$ is positively correlated with $\beta$. Therefore, controlling the contact rate $\beta$ will be an effective way to curb the spread of the epidemic.

Fig. 4

Long-term asymptotic dynamic behavior of model (2)

Fig. 5

Dynamic control strategy u(t) and dynamic contact rate ${\tilde{\beta }}(t)$

Note that the expression (3), ${\tilde{\beta }}$ represents the average contact rate, which is a constant. In Fig. 4, we also give four sets of fixed values of $\beta$, and set $u(t)=0$, which means that the average contact rate replaces the contact rate over the entire time interval. In fact, since the control strategy u(t) is a function of time t at the beginning of the epidemic, we should adopt strict control measures to limit the movement and exposure of the population. With a large number of investigations, including nucleic acid testing, isolation, and observation, or other measures, the epidemic has been controlled basically. At this time, it is also necessary to properly resume production to ensure the operation of the city and the normal life of residents. For this purpose, we construct a monotonically decreasing piecewise function with respect to time t as follows

$$\begin{aligned} u(t)=\left\{ \begin{aligned}&0.5, \qquad \qquad \qquad \,\,\tau _{1}=0\le t \le 6,\\&-\frac{1}{55}t+\frac{67}{110}, \,\,\qquad 6<t \le 17,\\&-\frac{1}{130}t+\frac{28}{65},\qquad 17 < t \le \tau _{2}=56. \end{aligned} \right. \end{aligned}$$

(6)

Table 7 Characteristic of data

The three-stage function in u(t) is based on the four sets of data, which is shown in (a) of Fig. (5). Note that the characteristics of the four sets of data are shown in Table 7. The spread of an epidemic can also be divided into three stages. The first stage represents the confirmation of the first case to the maximum increase in a single day. According to the four groups of data, we take the median as 6 days. At the end of the second stage, there are zero new cases, and we take the median as 17 days. At the end of the third stage, the last patient has recovered, which means the ending of the epidemic. The maximum time we take is 56 days. Based on the above analysis, (6) can represent a control strategy that changes over time and is divided into three stages. Further, we can calculate a dynamic change contact rate as follows, which is shown in (b) of Fig. (5).

$$\begin{aligned} {\tilde{\beta }}(t)=\beta -u(t)=\left\{ \begin{aligned}&0.1, \qquad \qquad \qquad \,\,\tau _{1}=0\le t \le 6,\\&\frac{1}{55}t-\frac{1}{110}, \,\,\qquad 6<t \le 17,\\&\frac{1}{130}t+\frac{11}{65},\qquad 17 < t \le \tau _{2}=56. \end{aligned} \right. \end{aligned}$$

To clarify the rationality of introducing a dynamic control strategy, we can calculate the average contact rate of ${\tilde{\beta }}(t)$ in the interval $[\tau _{1},\tau _{2}]=[0,56]$ as follows

$$\begin{aligned}&{\tilde{\beta }}=\frac{\int _{0}^{6}0.1\,\mathrm {d}t+\int _{6}^{17}\left( \frac{1}{55}t-\frac{1}{110}\right) \,\mathrm {d}t+\int _{17}^{56}\left( \frac{1}{130}t+\frac{11}{65}\right) \,\mathrm {d}t}{56}\\&=0.3634. \end{aligned}$$

The dynamic behavior of the model (2) at the contact rate ${\tilde{\beta }}(t)$ and ${\bar{\beta }}$ is shown in Fig. 6. Obviously, under the two equivalent control strategies, the control effect of ${\tilde{\beta }}(t)$ is better than that of ${\bar{\beta }}$. That is, the effect of the control strategy adjusted in time with the change of the epidemic is better than the fixed strategy of equivalent strength. Theorem 2 proved the existence of the optimal control strategy when considering the control cost. The control strategy (6) is an effective construction based on actual data, and the numerical simulation (Fig. 5) proves the good effect that can be achieved under this construction. This provides the disease control department with an actionable and effective control strategy suggestion.

Fig. 6

Long-term asymptotic dynamic behavior of model (2)

6 Conclusions

In this paper, we mainly focus on the spread and control of the second wave of epidemics in China. Different countries have different ideologies and adopt different strategies to deal with the spread of the epidemic. This has led to the failure of countries around the world to quickly form an effective control strategy, making the epidemic still spreading so far. Therefore, it is important to study the spread of the disease in the context of relevant national and regional control policies. The mathematical model established by scholars has theoretical guidance for epidemic control. Therefore, the established model must be combined with the actual situation of the country, and the proposed control strategy can be implemented.

In this work, we investigated the case data and regularity in four cities: Beijing, Liaoning, Urumqi, and Kashgar. Mining the regularity of the data in detail lays the foundation for the establishment of mathematical models and parameter selection for numerical simulation. Furthermore, a two-stage SC-SCIRS epidemic model with traceability characteristics and dynamic control strategy was established, and the dynamic behavior of the model was studied. Specifically, the existence and stability of the disease-free equilibrium point of the model and the sensitivity of the basic regeneration number to the parameters have been rigorously demonstrated. Additionally, considering the control cost and treatment cost, the existence of the optimal control strategy is proved. Numerical simulation verified and extended the theoretical results. In particular, we constructed a three-stage function in u(t) is based on the four sets of data. This control function can adjust the intensity in time based on the outbreak of the epidemic. This control function can adjust the intensity appropriately based on the outbreak situation of the epidemic. And through numerical simulation, it is proved that the effect of dynamic control strategy is better than that control strategy with fixed intensity. An important conclusion is that controlling the class contacts with others is an effective measure to curb the spread of the epidemic. In addition, a dynamic control strategy based on the regularity of actual data was constructed and its effectiveness was verified. This strategy is feasible and can provide feasible theoretical guidance for disease control departments.

The model established in this paper is closely integrated with China’s current epidemic management policy. For example, when a case is diagnosed, the official website will promptly report its trajectory and look for people in the same vehicle. This process corresponds to the two equations of the first stage in model (1). Because the model in this paper is based on existing data and policies, the epidemic in China has achieved good results and is consistent with the conclusions in the paper, which is the application and effective verification of our research results. Our research focuses on finding the optimal control strategy between epidemic control and economic development. This is a serious problem facing the world, especially in countries with more severe epidemics. In the future work, we will promote our research methods and results, establish epidemic models applicable to different national conditions and policies, and provide feasible suggestions for countries around the world to adopt effective control strategies.