1. 引言
2019冠状病毒病(COVID-19)是由严重急性呼吸系统综合征冠状病毒2型(SARS-CoV-2)引起的传染病,于2019年12月在中国武汉爆发,随后在短短几个月时间内在全球迅速传播,引发了各个国家的经济衰退和公共卫生安全危机。COVID-19患者的主要临床表现为干咳、胸痛、呼吸困难、腹泻等一系列症状,在一些患者中,甚至会引发神经系统并发症,威胁生命安全。由于其在全球范围内的快速传播和在特定群体中相对较高的死亡率,世界卫生组织(WHO)于2020年3月11日宣布2019冠状病毒病(COVID-19)为全球大流行。为了减缓病毒的传播和疫情的加重,封锁和隔离是早期控制疫情的有效方法,如人们被要求呆在自己的家中自我隔离、保持社交距离、限制旅行活动等等 [1] [2] [3] [4]。因此,检测COVID-19爆发的早期预警信号以便及时采取公共卫生策略来减少流行病的传播和破坏显得至关重要。然而,生物系统和社会系统的复杂特性给实现实时预测传染病爆发带来了巨大的挑战。此外,用于这种检测的监控系统可能是成本高昂的,从而导致在许多缺乏公共卫生基础设施的国家中未能检测到流行病的潜在变化 [5] [6]。机器学习方法已经在预测领域得到发展 [7] [8],但是当样本数量有限时,通常无法预测传染病的爆发。统计数学模型已经被提出来描述当前COVID-19流行病的传播 [9] [10] [11],这有助于临床医生了解其传播情况。但是,与时间序列数据预测不同的是,传染病爆发是典型的非线性事件,其特征是从逐渐变化到剧烈过渡发展,这使得预测COVID-19的爆发变得非常困难。因此,开发一种有效的无模型方法来直接预测此类非线性事件或基于实时数据(例如每日新增病例)来检测传染病爆发的预警信号具有重要意义。
在本文中,COVID-19的传播被视为随时间且具有临界点的非线性动力学系统 [12],在临界点处,该系统通过临界转变进入大规模疾病爆发状态。人们普遍认为,COVID-19爆发的动态进程可以描述为三个阶段 [13] [14] [15],即正常阶段、前爆发阶段和爆发阶段,其中前爆发阶段被认为是导致大规模且可能无法控制的流行病爆发的关键转变之前的临界点。在只有少数病例的前爆发阶段,可以通过适当措施控制疾病传播,但是,如果疾病在没有或很少采取遏制措施的情况下持续传播,那么病毒的泛滥和大量的病例将会给政府部门带来难以克服的困难,从而导致不可逆转的地方性流行病甚至全球性大流行病。因此,在前爆发阶段检测出流行病爆发的预警信号至关重要。为了刻画和预测这种转变,本文采用了一种有效的计算方法,即网络熵(LNE)方法,以检测COVID-19爆发的预警信号,这种方法只需要地理区域网络和日增病例高维数据的信息。具体而言,基于区域网络和日增病例高维数据的组合来挖掘动态信息,LNE方法可以定量地表征区域网络中传染病的传播,从而检测出COVID-19爆发的早期预警信号。LNE方法以动态网络标志物(DNM)或动态网络生物标志物(DNB)为基础 [14] [15] [16],在理论上已经趋于完善。DNM概念已应用于多种情形,例如:识别细胞分化的临界点 [17]、检测流感爆发的预警信号 [13] 等。当动力系统接近临界点时,DNM理论表明,观测变量的一小部分(DNM元素)将高度相关地剧烈波动,从而通过几个统计指标传达即将发生的临界转变的预警信号,即DNM组中元素之间的相关性急剧增加;所有DNM元素的偏差值将集体迅速增加。
与时间序列预测或爆发阶段的传统检测不同,网络熵方法的目的是识别前爆发阶段或临界阶段,这种阶段通常没有明显的异常,但在不久的将来很有可能转变为灾难性事件。特别地,与传统方法相反,这项工作的主要特征是利用网络中的高维动态信息来提供可靠的预测。作为一种无模型的非线性事件预测方法,网络熵分别应用于中国湖北省(包括武汉)、日本关东地区、巴西部分地区等三个区域的每日病例数据,并在整体和局部上都检测到了COVID-19爆发的预警信号,证实了网络熵方法的有效性和准确性。
2. 网络熵(LNE)方法
LNE方法以DNB理论为理论背景 [18],用离散动力系统表示区域网络的动态发展过程,在其满足某些特定假设条件的情况下存在分岔或者临界点,当系统接近临界点时,至少会出现一个主导组(即动态网络标志物),其中元素的剧烈波动且高度相关意味着即将过渡到爆发阶段。
3. 计算网络熵算法流程
为了检测COVID-19爆发的预警信号,网络熵方法的过程包括以下三个步骤,流程图如图1所示。
(i) 构建区域/城市网络结构
在一个国家/地区中,将区域的地理分布及其相邻信息建模为一个网络,其中每个节点代表一个区域。基于地理和交通信息,在这种网络中的两个相邻区域之间存在一条边,表示它们的邻接和交互关系,如图1(a)所示。一个区域网络可以被划分为多个局部网络,每个局部网络由一个中心结点和它的一阶邻居构成。对于一个有着地区网络
和
个子地区/结点
的区域,假设存在
个局部网络
,局部网络
以结点
为中心,有
个一阶邻居
。实际上,我们根据地区之间的主要交通方式及其特定地理位置来构建一块区域的区域网络。
(ii) 计算各个局部网络的网络熵指标
对于任意区域网络,本文将滑动窗口
的长度设定为
其中
是区域网络的平均度并且由于每个结点自相关,所以再添加常数1。
,
表示区域
在时间点
的日增确诊人数。
对于有着
个成员的局部网络
,即一个中心结点
和
个一阶邻居
,它在样本点 处的网络熵指标可从熵增和偏差的角度计算如下:
(1)
其中
(2)
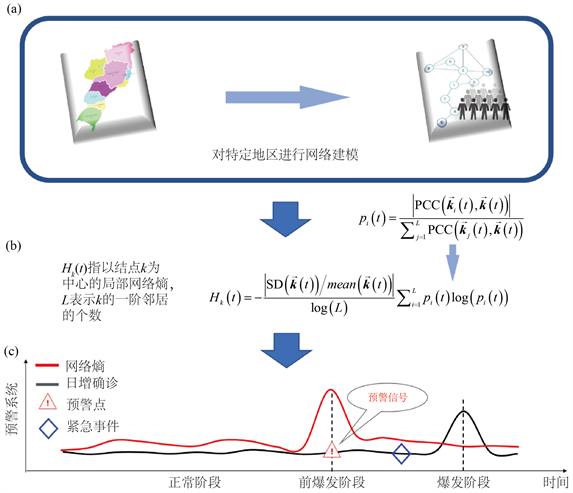
Figure 1. (a) Modeling for regions; (b) Calculation of landscape network entropy in the local area; (c) Dynamic changes of landscape network entropy during the spread of COVID-19
图1. (a) 地区建模;(b) 局部地区网络熵的计算;(c) COVID-19传播过程中网络熵的动态变化
表示中心结点
和其一阶邻居
在样本点
处的皮尔逊相关系数,
表示中心结点
在样本点
时候的日增病例标准差,
为中心结点
在
时刻的日增病例均值。理论上,当系统在分岔点附近的时候,即当时间点
逼近临界阶段时,DNM元素会表现出明显的集体行为,并具有较大的相关波动。因此,在局部网络中,若所有结点都是DNM元素,那么所有元素的相关系数都会急剧增加(比如
),而当系统接近爆发点的时候概率
会变得更加平均,从而网络熵指标大幅增加。此外,等式(1)中
也会提升局部网络
的网络熵指标。因此,网络熵指标可以定量地描述每个局部网络的临界状态,也就是说,可以通过网络熵指标检测关键转变的预警信号。之后再对各个局部地区的网络熵求平均值即可计算得到整体地区的网络熵。
(iii) 识别前爆发阶段
应用单样本
检验 [19] 来确定常数
在统计上是否显著不同于
维向量
的均值。单样本
检验统计量由以下公式定义:
(3)
表示向量
的均值,
表示向量
的标准差。统计指标
定量地测量
和
之间的显著差异。为了估计统计显著性,可以通过
分布获得
值
(与 相关的概率)。如果
,则
和
之间存在显着差异,否则差异不显着。在本文中,为了基于网络熵指标准确分析监测COVID-19传播的动态进程,单样本
检验被应用于确定临界点的出现。
当网络熵指标
与向量
的均值显著不同时(
),时间点
被视为临界点。通过 检验我们将网络熵指标转换为其对应的倒数
。因此,网络熵指标的阈值设定为20,对应于显著性水平
。若网络熵指标低于阈值,那么时间点
被认为是正常阶段,然后选择下个时间点
继续进行新的测试。
网络熵方法旨在灾难性转变到爆发阶段前识别检测出前爆发阶段。本文的研究理论背景是基于DNM理论,该理论旨在根据观测到的高维数据定量识别检测出复杂系统进程中的关键阶段(临界点)。一般来说,从复杂系统的角度上看,COVID-19传播爆发的动态过程可以用具有分岔点的非线性动力系统的时间演化来描述,在分岔点上系统发生剧烈的转变 [20] [21]。
4. 应用
我们将此方法应用于以下3个区域的日增确诊病例数据:
(i) 中国湖北(https://github.com/BlankerL/DXY-COVID-19-Data)
(ii) 日本关东地区(https://www.mhlw.go.jp/index.html)
(iii) 巴西10个州(https://covid.saude.gov.br/)
对于给定的区域网络,根据等式(1)计算每个局部网络的网络熵指标。每天根据所有局部网络的平均LNE指标来定量检测该区域从正常阶段到爆发阶段的关键过渡的预警信号。每日新增病例的急剧上升被定义为疾病的爆发点,表明出现了灾难性流行病。对于短时间内有多个预警点的地区,我们将第一个点标记为预警信号。于是有以下结果:
4.1. 中国湖北
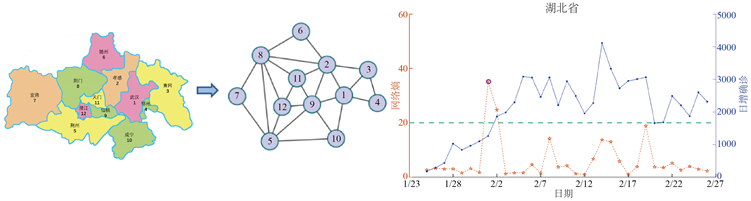
根据湖北省12个城市的地理分布建立了12个节点的网络(图2(a))。基于从2020年1月25日到2020年2月26日的每日新增新冠病例,计算每个局部网络的网络熵指标,然后利用平均网络熵指标来识别湖北省COVID-19传播的信号点。如图2(b)中的橘黄色曲线所示,由网络熵指出的带有紫红色圆圈的第一个警告点出现在2月1日,早于日增病例暴涨的发生(图中的蓝色曲线)。此外,图2(c)也显示了湖北省各个城市的局部网络熵指标曲线。显然,由网络熵指出的相应信号点(红色圆圈)都领先于各个城市的日增病例的急剧增长(COVID-19爆发)。
4.2. 日本关东地区
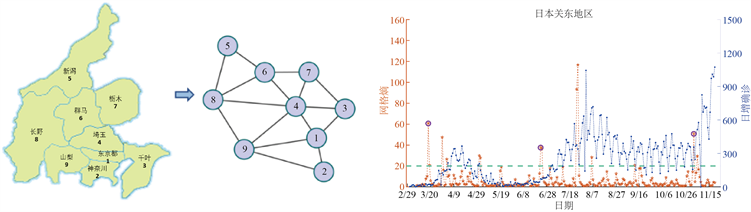
本文收集了2020年3月2日至2020年11月21日日本关东地区9个县的每日新增COVID-19病例数据。根据关东地区的地理邻接信息,建立了一个九节点网络(图3(a))。如图3(b)所示,紫红色圆圈标记的第一个预警点出现在3月18日,表明此后即将迎来COVID-19爆发的关键转变,即从3月26日起每
 (a) (b)
(a) (b)  (c)
(c)
Figure 2. Real-time monitoring of COVID-19 spread and outbreak in Hubei Province of China. (a) An twelve-node network of Hubei; (b) The LNE index (the red curve) and the number of daily new cases (the blue curve) in Hubei; (c) The local LNE indices for eight districts
图2. COVID-19在湖北省传播和爆发的数据监控。(a) 湖北的十二个网络节点;(b) 湖北省LNE指标(红线)和日增病例数量(蓝线);(c) 8个子地区的局部LNE指标
天的新病例急剧增加(图3(b)中的蓝色曲线)。日本政府于4月7日正式宣布全国紧急事件声明以应对COVID-19确诊人数激增 [22],这一事件也证实了预警信号点的有效性。值得注意的是,在5月1日有一个预警信号,指示着很快被控制住的第一波疫情的临界点。经过大约两个月的抗击流行病后,日本政府正式宣布结束COVID-19紧急状态。然而,在第二波COVID-19爆发以及政府紧急报告发布之前(例如,“东京于6月30日修订了COVID-19监测系统指南 [23] ”,“随着疫情的恢复,东京于7月15日将病毒警报提高到了最高水平 [24] ”),于6月23日又发出了另一个预警信号。此外,在日本政府于9月25日宣布重新开放边界 [25],并于10月7日恢复双边商务旅行后 [26],于11月2日检测到第三个预警信号,随后出现的新增确诊人数大潮验证了这一信号的有效性。11月19日,当局将东京的COVID-19警报提升到了最高级别 [27]。
 (a) (b)
(a) (b) 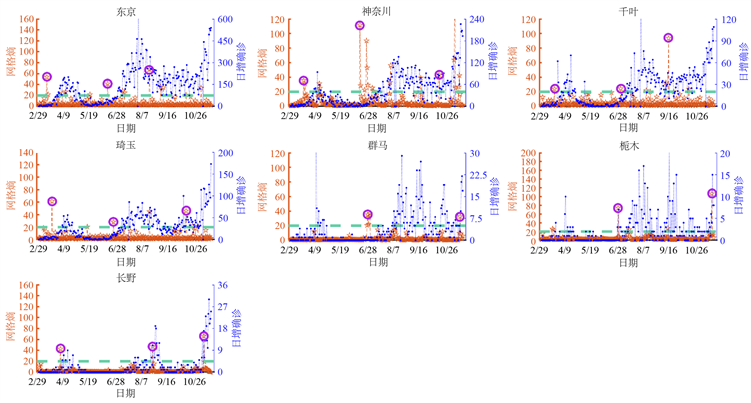 (c)
(c)
Figure 3. Real-time monitoring of COVID-19 spread and outbreak in the Kanto region of Japan. (a) An nine-node network of the Kanto region; (b) The LNE index (the red curve) and the number of daily new cases (the blue curve) in the Kanto region; (c) The local LNE indices for seven districts
图3. COVID-19在日本关东地区传播和爆发的数据监控。(a) 关东地区的九个网络节点;(b) 关东地区LNE指标(红线)和日增病例数量(蓝线);(c) 7个子地区的局部LNE指标
此外,关东地区七个子地区特定网络熵指数也检测到了COVID-19爆发的预警信号(图3(c))。对于这些地区,LNE指数也能预警疾病的爆发,例如,在东京,分别在3月14日和6月15日出现第一个和第二个信号传递点(紫红色的圆圈),此后该城市每天的新增病例急剧增加。因此,在日本关东地区,网路熵方法可以在灾难性转变到COVID-19爆发阶段之前识别临界状态。
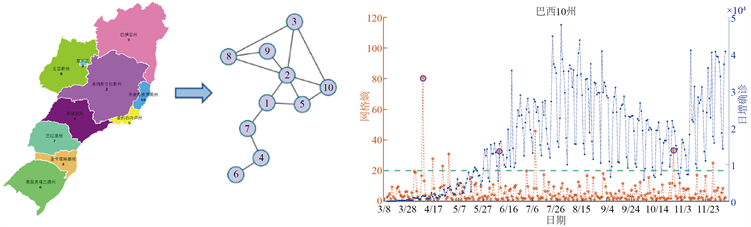
4.3. 巴西10个州
本文搜集了从2020年3月10日到2020年12月9日期间巴西10个疫情严重的州的COVID-19新增病例数据。根据巴西各州的地理位置分布,并考虑到其主要交通运输方式是公路,我们构建了一个由10个节点组成的邻接网络(图4(a))。如图4(b)所示,网络熵指出的第一个预警信号出现在4月8日,预示此
 (a) (b)
(a) (b) 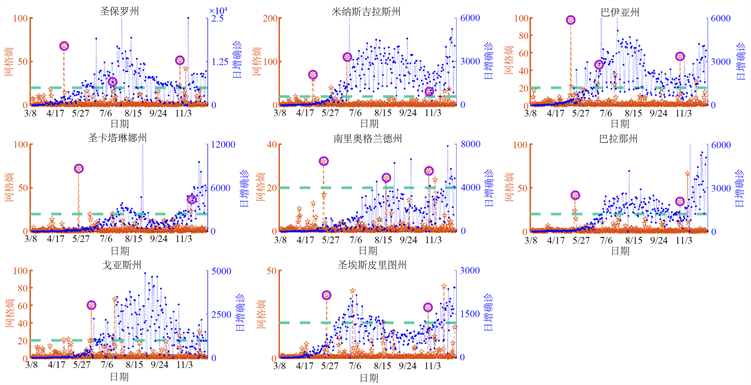 (c)
(c)
Figure 4. Real-time monitoring of COVID-19 spread and outbreak in 10 Brazil states with severe epidemics. (a) An ten-node network of these states; (b) The LNE index (the red curve) and the number of daily new cases (the blue curve) in 10 Brazil states; (c) The local LNE indices for eight districts
图4. COVID-19在巴西10个州内传播和爆发的数据监控。(a) 巴西10州的10个网络节点;(b) 巴西的LNE指标(红线)和日增病例数量(蓝线);(c) 8个子地区的局部LNE指标
后即将爆发疫情。而正是在这一天,巴西官方发布了警报信息,将旅游和行动限制延长至4月下旬 [28]。6月9日检测到第二个预警信号,随后圣保罗州州长于6月26日宣布延长现行的检疫措施时限 [29]。第三个预警信号则出现在10月28日,此后,巴西有关当局宣布延长陆地及海上边界禁令至12月份 [30],显示了这一信号的有效性。
为了验证网络熵指标的普适性,我们还计算了各州的网络熵指数来识别每个州的COVID-19前爆发阶段(图4(c))。在每日新增病例急剧增加之前,网络熵指数已成功为8个州确定了各个预警信号点,例如,在圣保罗州,第一个、第二个和第三个信号点分别出现在4月29日,7月15日和10月29日,这表明即将出现的三波新增确诊人数暴涨。
5. 总结
COVID-19在世界各地迅速蔓延,并在短短几个月内发展成全球性流行病,这极大地威胁到了人们的生命健康安全并造成了巨大的经济损失 [31]。为了迅速、正确地应对传染病爆发,决策者和政策制定者需要及时准确地进行预警。因此,为了对抗COVID-19的传播和爆发,建立一个基于区域网络和相关卫生部门发布的每日新增病例数据的实时监控系统非常重要。与时间序列数据预测不同,传染病爆发是非线性事件,通常很难准确预测。在本文中,我们基于地区网络和每日新增病例数据的信息,使用了一种有效的非线性方法,即网络熵方法,以识别疫情严重恶化前的前爆发阶段。该方法在三个地区表现良好:中国湖北省,日本关东地区和巴西10个州。网络熵指标预测的临界信号点是出现在每日新增病例急剧增加之前(COVID-19爆发点),为实施疫情防控政策以控制COVID-19的传播和爆发提供了适当的时间依据。
网络熵方法具有明显的优势。一方面,网络熵不同于需要大量训练样本的传统机器学习方法,它是一种无模型的非线性方法,这意味着既没有特征选择也没有参数训练过程,从而避免了过拟合问题。另一方面,与传统的DNM方法相比,网络熵方法已得到改进并应用于宏观地理网络,结合区域网络的动态信息可以更加准确可靠地检测出前爆发阶段。实际上,整体地利用整个网络中数据的高维动态信息来提供可靠的预测是此方法的主要特征之一。因此,网络熵方法是数据驱动的,在公共卫生管理的实时监控中具有很高的利用价值。
不过,有几个因素会影响所提出的LNE方法的性能:1) 日增病例不准确会导致出现错误预警(错误阳性信号)和不敏感的网络熵指数(错误阴性信号)。2) 当应用于实时数据时,病例报告时间上发生延迟可能会导致出现无效信号。这些是大多数数据驱动方法的常见局限性,可以通过将其与有效的基于模型的方法相结合来解决。
基金项目
本文受广东省基础与应用基础研究基金(No. 2021A1515012317)资助。