Evaluation of Bayesian Deep Learning Methods for Quantifying Uncertainties in Forecasting Deaths from COVID-19

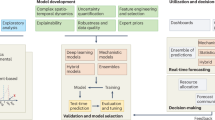
Abstract

The scenario of epidemic forecasting with inflection points and constant changes in population behavior is extremely critical. This way, there is a growing consensus in the process of modeling infectious diseases that forecasts should not only indicate a single point outcome but also quantify their own uncertainty. In this regard, our study investigated uncertainty quantification in the prediction of COVID-19 deaths, using Bayesian Deep Learning techniques and producing prediction intervals as an informational mechanism to address the unpredictability of external factors. Six distinct methods were employed: MC Dropout, Concrete Dropout, Spatial Dropout, MC-DropConnect, SG-HMC, and SWAG. Through regression heteroscedastic modeling, the approaches were tested and their results compared, particularly in periods with intermittent waves. The methodology initially emphasized building a robust database with an excellent representation of the problem. Subsequently, the experiments focused on forecasting daily intervals of the 7-day moving average, at the 28-day horizons, for the five most populous U.S. states, over a period of 1 year. Regarding the results, SWAG achieved the best results in the Log-Likelihood metric, while Spatial Dropout performed best in the MSE. The Concrete Dropout produced conservative predictive intervals with high coverage, above 85% using amplitudes between 13% and 34%. During the epidemiological wave, there was greater instability in the uncertainty estimation process, as evidenced by a reduction in the Log-Likelihood metric. The findings contribute to the maturity of a tangible and assertive perspective on uncertainty estimation in DL, facilitating decision-making in the dynamic environment of epidemic modeling.