Skip to main content

Advertisement

Springer Nature Link
Log in

Mathematical modeling and stability of SARS-CoV-2 transmission dynamics among domestic tourists in Thailand

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

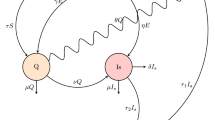
Abstract

The defined epidemiological model system explaining the spread of infectious diseases characterized with SARS-CoV-2 is analysed. The resulting SEIQR model is analysed in a closed system. It considers the basic reproductive value, the equilibrium point, local subclinical stability of the disease-free equilibrium point and local subclinical stability of the endemic equilibrium point. This is examined and the asymptotic dynamics of the appropriate model system are investigated. Further, a sensitivity analysis supplemented by simulations is prepared in advance to impose how changes in parameters involve the dynamic behaviours of the model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Data availability

The data used to support the findings of this study are available from the corresponding author request.

References

  1. WHO: Coronavirus disease 2019 (COVID-19). Situation report 202251. (2022)

  2. Bureau of Epidemiology. Department of Disease Control, Ministry of Public Health. Thailand 2022. Available form: http://www.boe.moph.go.th/fact/Covid-19.htm

  3. Moore, S.E., Okyere, E.: Controlling the transmission dynamics of COVID-19. Commun. Math. Biol. Neurosci. 2022, 1–13 (2022)

    MATH  Google Scholar 

  4. Fang, Y., Nie, Y., Penny, M.: Transmission dynamics of outbreak and effectiveness of government interventions: a data-driven analysis. J. Med. Virol. 92, 645–659 (2020). https://doi.org/10.1002/jmv.25750

    Article  MATH  Google Scholar 

  5. Liu, Z., Magal, P., Seydi, O., Webb, G.: Understanding unreported cases in the 2019-nCov epidemic outbreak in Wuhan, China and the importance of major public health interventions. Biology 9, 50 (2020). https://doi.org/10.3390/biology9030050

    Article  MATH  Google Scholar 

  6. Daw, M.A.: Modelling the epidemic spread of COVID-19 virus infection in Northern African countries. Travel Med. Infect. Dis. 2020(35), 101671 (2020). https://doi.org/10.1016/j.tmaid.2020.101671

    Article  MATH  Google Scholar 

  7. Unlu, U., Yalcin, N., Avsarlıgil, N.: Analysis of efficiency and productivity of commercial banks in Turkey pre- and during COVID-19 with an Integrated MCDM approach. Mathematics 10(13), 2300 (2022). https://doi.org/10.3390/math10132300

    Article  MATH  Google Scholar 

  8. Harir, A., Malliani, S., et al.: Solutions of conformable fractional-order SIR epidemic model. Int. J. Diff. Equ. 2021, 7 (2021). https://doi.org/10.1155/2021/6636686

    Article  MathSciNet  MATH  Google Scholar 

  9. Sookaromdee, P., Wiwanitkit, V., et al.: Imported cases of 2019-novel coronavirus (2019-ncov) infections in Thailand: mathematical modelling of the outbreak. Asian Pac J Trop Med 13(3), 139–140 (2020)

    Article  MATH  Google Scholar 

  10. Cruz-Lopez, Flora, Garza-González, Elvira, et al.: Analysis of influenza and dengue cases in Mexico before and during the COVID-19 pandemic. Infect. Dis. (2021). https://doi.org/10.1080/23744235.2021.1999496

    Article  MATH  Google Scholar 

  11. Deborah, D.: Mathematical model for the transmission of Covid -19 with nonlinear forces of infection and the need for prevention measure in Nigeria. J. Infect. Dis. Epidemiol. 6(5), 158 (2020). https://doi.org/10.23937/2474-3658/1510158

    Article  MATH  Google Scholar 

  12. Khader, M.M., Adel, M.: Modeling and numerical simulation for covering the fractional COVID-19 model using spectral collocation-optimization algorithm. Fractal Fract. 6, 363 (2022). https://doi.org/10.3390/fractalfract6070363

    Article  MATH  Google Scholar 

  13. Liu, G., Chen, J., Liang, Z., Peng, Z., Li, J.: Dynamical analysis and optimal control for a SEIR model based on virus mutation in WSNs. Mathematics 9, 929 (2021). https://doi.org/10.3390/math9090929

    Article  MATH  Google Scholar 

  14. Martinot, M., Schieber, A., et al.: Clinical features and outcomes in adults with COVID-19 during the pre-omicron and omicron waves. Infect. Dis. 2024(54), 104833 (2024). https://doi.org/10.1016/j.idnow.2023.104833

    Article  Google Scholar 

  15. Harir, A., Melliani, S., et al.: Variational iteration method and differential transformation method for solving the SEIR epidemic model. Int. J. Diff. Equ. 2020, 7 (2020). https://doi.org/10.1155/2020/3521936

    Article  MathSciNet  MATH  Google Scholar 

  16. Sungchasit, R., Tang, I.M., Pongsumpun, P.: Mathematical modeling: Global stability analysis of super spreading transmission of respiratory syncytial virus (RSV) disease. Computation 10(7), 120 (2022). https://doi.org/10.3390/computation10070120

    Article  MATH  Google Scholar 

  17. Mwalili, S., Kimathi, M., Ojiambo, V., Gathungu, D., Mbogo, R.: SEIR model for COVID-19 dynamics incorporating the environment and social distancing. BMC Res. Notes 13(1), 352 (2020). https://doi.org/10.1186/s13104-020-05192-1

    Article  MATH  Google Scholar 

  18. Wintachai, P., Prathom, K.: Stability analysis of SEIR model related to efficiency of vaccines for COVID-19 situation. Heliyon 7(4), E06812 (2021). https://doi.org/10.1016/j.heliyon.2021.e06812

    Article  MATH  Google Scholar 

  19. Chen, T.M., et al.: Mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect. Dis. Poverty 9, 24 (2020)

    Article  MATH  Google Scholar 

  20. Riyapan, P., Shuaib, S.E., Intarasit, A.: A mathematical model of COVID-19 pandemic: a case study of Bangkok, Thailand. Comput. Math. Methods Med. 2021(1), 11 (2021). https://doi.org/10.1155/2021/6664483

    Article  MATH  Google Scholar 

  21. Sameni, R.: Mathematical modeling of epidemic diseases; a case study of the COVID-19 coronavirus. arXiv: 2003.11371v3[q-bio.PE] 19 May 2020

  22. Kim, B.N., Kim, E., Lee, S., Oh, C.: Mathematical model of COVID-19 transmission dynamics in South Korea: the impacts of travel restrictions, social distancing, and early detection. Processes 8(10), 1304 (2020). https://doi.org/10.3390/pr8101304

    Article  MATH  Google Scholar 

  23. Sharma, S., Volpert, V., Banerjee, M.: Extended SEIQR type model for COVID-19 epidemic and data analysis. Math. Biosci. Eng. 17(6), 7562–7604 (2020). https://doi.org/10.3934/mbe.2020386

    Article  MathSciNet  MATH  Google Scholar 

  24. Brauer, F., Castillo-Chavez, C.: Mathematical models in population biology and epidemiology. Springer, New York, NY (2012)

    Book  MATH  Google Scholar 

  25. Busenberg, S., Cooke, K.: Vertically transmitted disease. Springer, Berlin, Heidelberg (1993)

    Book  MATH  Google Scholar 

  26. Cruz-Pacheco, G., Esteva, L., Montano, J.A., Vargas, C.: A Mathematical model for the dynamics of west Nile Virus. IFAC Proc. Vol 37(21), 475–480 (2004)

    Article  MATH  Google Scholar 

  27. van den Driessche, P., Watmough, James: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180(1–2), 29–48 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  28. Nainggolan, J., Ansori, M.F.: Stability and sensitivity analysis of the COVID-19 spread with comorbid diseases. Symmetry 14, 2269 (2022). https://doi.org/10.3390/sym14112269

    Article  MATH  Google Scholar 

  29. Dielman, D., Heesterbeek, J.: Mathematical epidemiology of infectious disease: model building analysis and interpretation. Wiley Series in Mathematical and Computation Biology. Wiley, Chichester (2000)

    MATH  Google Scholar 

  30. Olaniyi, S., Lawal, M.A., Obabiyi, O.S.: Stability and sensitivity analysis of a deterministic epidemiological model with pseudo-recovery. IAENG Int. J. Appl. Math. 46(2), 160–167 (2016)

    MathSciNet  MATH  Google Scholar 

  31. Naik, P.A., Owolabi, K.M., Zu, J., Naik, M.U.D.: Modeling the transmission dynamics of COVID-19 pandemic in caputo type fractional derivative. J. Multiscale Model. 12(03), 2150006 (2021). https://doi.org/10.1142/S1756973721500062

    Article  MathSciNet  MATH  Google Scholar 

  32. Karaagac, B., Owolabi, K.M., Pindza, E.: A computational technique for the Caputo fractal-fractional diabetes mellitus model without genetic factors. Int. J. Dyn. Control 11, 2161–2178 (2023). https://doi.org/10.1007/s40435-023-01131-7

    Article  MathSciNet  MATH  Google Scholar 

  33. Bhatter, S., Jangid, K., Abidemi, A., Owolabi, K.M., Purohit, S.D.: A new fractional mathematical model to study the impact of vaccination on COVID-19 outbreaks. Decis. Anal. J. 6, 100156 (2023). https://doi.org/10.1016/j.dajour.2022.100156

    Article  MATH  Google Scholar 

  34. Mishra, A.M., Purohit, S.D., Owolabi, K.M., Sharma, Y.D.: A nonlinear epidemiological model considering asymptotic and quarantine classes for SARS CoV-2 virus. Chaos, Solitons Fractals 138, 109953 (2020). https://doi.org/10.1016/j.chaos.2020.109953

    Article  MathSciNet  MATH  Google Scholar 

  35. Idisi, O.I., Yusuf, T.T., et al.: A bifurcation analysis and model of Covid-19 transmission dynamics with post-vaccination infection impact. Healthcare Anal. 2023(3), 100157 (2023). https://doi.org/10.1016/j.health.2023.100157

    Article  MATH  Google Scholar 

Download references

Acknowledgements

The authors thank the handling editor and anonymous referees for their valuable comments and suggestions which led to an improvement of our original paper. The first author would like to thank Research and Development Institute and Faculty of Science and Technology, Phuket Rajabhat University. The second author was supported by King Mongkut’s Institute of Technology Ladkrabang.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, Phuket Rajabhat University, Phuket, Thailand

    Rattiya Sungchasit

  2. Department of Mathematics, School of Science, King Mongkut’s Institute of Technology Ladkrabang, Bangkok, Thailand

    Puntani Pongsumpun

Authors
  1. Rattiya Sungchasit
    View author publications

    Search author on:PubMed Google Scholar

  2. Puntani Pongsumpun
    View author publications

    Search author on:PubMed Google Scholar

Corresponding author

Correspondence to Puntani Pongsumpun.

Ethics declarations

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sungchasit, R., Pongsumpun, P. Mathematical modeling and stability of SARS-CoV-2 transmission dynamics among domestic tourists in Thailand. J. Appl. Math. Comput. 71, 173–202 (2025). https://doi.org/10.1007/s12190-024-02228-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-024-02228-8

Keywords

Mathematics Subject Classification