Introduction

Since December 2019, COVID-19, which is a disease caused by the novel beta-coronavirus known as severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), has caused huge concern to people and countries around the world1. This is not the first time that Coronaviruses have afflicted humans. However, objective factors such as geography, temperature and effective control measures introduced by national governments have in the past limited the spread of acute virus infections to keep them endemic, as in the cases of severe acute respiratory syndrome (SARS), Middle East respiratory syndrome (MERS), Hendra, Nipah and Ebola2.

However, the high mutagenicity, contagiousness3, and inconsistent case fatality rate (CFR) of COVID-194 caused its original strain and several variants to break through regional boundaries and sweep through the world. After the original type of SARS-CoV-2 was first reported in Wuhan, China, in December 2019, the number of infections increased rapidly, and most countries detected COVID-19 cases within two months of the first outbreak. Since then, the genes of the virus have evolved to produce different strains5. Some variants spread only in particular areas and accounted for small proportions of the total number of cases, such as beta (B.1.351), gamma and lambda. Nevertheless, three variants became the sources of the majority of COVID-19 cases in their periods of dominance: alpha (B.1.1.7), found in England in September 20206; delta (B.1.617.2), found in India in October 20207; and omicron, found in South Africa in November 2021 (B.1.1.529)8. Omicron is now the dominant variant among new cases in all countries9. So far, nearly 550 million people have been diagnosed with COVID-19, and 6.3 million deaths have been confirmed10.

Various countries sounded alarms regarding public health defense against the virus and its variants. Throughout the COVID-19 pandemic, most countries have taken active measures to curb the spread of infectious diseases by initiating policies such as lockdowns, 14-day quarantine of those with the disease, antigen and nucleic-acid testing, and requirements for social distancing. According to the accepted principles of virus transmission, the screening of contacts and minimization of the transmission route can limit the passage of infectious viruses11, which indicates that the severity of national policies will influence the number of new outbreaks in that country. However, even though lockdowns and requesting that citizens stay at home are highly effective measures, these are not long-term solutions given the effects on factors such as economics and education. Moreover, because each country/region has different geography, national conditions, economic situations and emphases on epidemic prevention, the effectiveness of such measures varies even among countries that impose the same restrictions. Therefore, investigation and prediction of the impact of various countries’ pandemic prevention policies on the development of new cases of COVID-19 in the context of their national situations may provide insights on how to streamline less important pandemic prevention policies in the selected regions.

To evaluate the relationship between the number of daily new confirmed COVID-19 cases and other objective factors, machine learning (ML) techniques can be useful. However, to achieve satisfactory performances, ML models often need large volume of data because their principles involve finding patterns from data. In the early stages of the pandemic, many areas lacked sufficient data on the number of infected patients and had inadequate response standards due to inadequate testing and medical systems. Thus, many models were developed to be used to predict the numbers of cases so that national governments could consider appropriate preventive measures. Currently, the types of COVID models that are commonly used are: the susceptible, exposed, infected, recovered (SEIR) or the susceptible, infected, recovered (SIR) methods; agent-based systems; and curve-fitting models12,13. SEIR/SIR models are based on mathematical descriptions of epidemic diseases. Scholars have continuously improved these over hundreds of years through the inclusion of characteristics of different infectious diseases14,15,16,17,18. The three categories of people that were included in the original SIR model susceptible, infected and recovered individuals19—were increased to four with the addition of exposed, infected but not yet infectious individuals during consideration of the characteristic incubation period of COVID-19 in the SEIR model. Hence, the SEIR model is currently generally applied to calculate COVID-19 predictions20. Agent-based models focus on events that will impact the spread of COVID-19, such as prevention policies instigated by governments21. Moreover, many investigators applied ML techniques to evaluate the complex variation of behavior and to predict COVID-19 transmission according to behavior theories, such as the multi-layered perceptron (MLP) model and the adaptive neuro-fuzzy inference system (ANFIS)22. On top of the first two models, curve-fitting models provide more comprehensive predictions than other methods because scholars add different parameters and variables that may directly or indirectly influence disease transmission23. Such models will focus more on the use of deep learning (DL), which is an advanced form of ML.

DL offers the ability to extract features that are provided by many connected layers. This makes it one of the most powerful sub-branches of ML. Long short-term memory (LSTM) model is a type of DL model good at analyzing long sequences of data. It can be used to analyze sequences based on their order and to ‘remember’ or ‘forget’ some specific parts of the data to improve the reasonableness of the predictions24. As the most popular variant of recurrent neural networks (RNNs), LSTM can solve vanishing gradient problem and process long-term dependencies in sequences better compared with the original RNN. Researchers who have investigated which model better predicts the number of cases related to COVID-19 generally agree that LSTM works well for predictions that feature time series. Shahid et al.25 have surveyed the efficiency of four forecast models for time series predictions of confirmed cases, deaths, and recoveries in ten major countries affected by COVID-19 for six months. This research showed the overriding performance of LSTM and its variant models, especially Bi-LSTM, which outperformed all models on three error measures.

Based on the existing prediction tools, many researchers are committed to using different prediction tools in different regions of a country or in a few numbers of countries to predict the epidemic period in a short-time span. Yang et al.26 focused on the pattern of disease transmission and China’s local policies to predict the active infections and new confirmed cases in Shanghai, Wuhan and other representative cities for about two months. Chandra et al.27 use LSTM and its extended models to capture the COVID-19 wave in Indian states in three period in two years, each period is about 4 months. Besides, Ketu28 and his team used a CNN-LSTM hybrid DL model to correctly forecast the COVID-19 epidemic across India by using around 5 months data in 2020. Alassafi et al.29 used daily confirmed cases and deaths data from Saudi Arabia, Morocco and Malaysia to verify the accuracy of LSTM model in COVID-19 predicting. From the above literatures, it is clear that multiple studies on prediction of Covid-19 new cases and daily death number have been performed but lack testing the commonly used forecasting models in more countries with various factors in a long-time span.

To assess the impact on the numbers of new cases of different COVID-19 prevention policies in each country/region, this study simulated the case scenarios and predicted the future numbers of infections mainly with LSTM. Specifically, we first split the collected 44 features into four groups: pandemic information, the characteristics of countries/regions, climate, and prevention policies. Pandemic information contained the features directly related to COVID-19, such as the new cases in different statistic pattern, the vaccination data, the mortality, the dominating variant, and etc. The characteristics of countries/regions included some basic information such as gross domestic product (GDP), population, and etc. Climate included temperate and humidity. Prevention policies covered 12 kinds in total and classified by the strict degrees in different areas and periods. Then, we did feature selection based on contributions of different features and different days before the prediction period. The contributions, or importance, were defined as the feature importance for gradient boosting machine (GBM), which is easily available and able to roughly locate the potential helpful features. Next, the 15 countries/regions were split into 14 training ones and 1 testing ones, which was repeated for 15 times so that we can achieve the testing results for every country/region. Among the data of each training country/region, we needed to select the data in a short period as the validation set to help control the number training epochs and avoid over-fitting. To ensure the generalization over different time frame, we divided the complete investigated period (about 900 days) into 14 overlapped short periods, each of them occupied around 20 percent time span, and we randomly assigned each to a training country/region. Data of each country/region in the assigned period are combined as a validation set, and the left data consisted of the training set. Finally, we trained multiple LSTM models with different training/testing partitions and different feature combinations. Moreover, support vector regressors (SVRs) and temporal convolutional networks (TCNs) were also used as comparison models.

We aim to provide insights regarding future precautionary measures to various national governments. Moreover, because many factors can affect the spread of COVID-19, we also considered the rigor of different policies, the economic situations of governments, the local population, the climate, and the prevailing local variants of COVID-19.

Results

The primary purpose of this study was to investigate the effect of different features on the modeling on the total number of new confirmed COVID-19 cases over the 14 days following the data period using LSTM models. The models involved the use of four data groups: pandemic information, countries/regions’ basic information, climate, and pandemic prevention policies (Table S1). Any hidden relationship that would be discovered between policy responses and the number of new confirmed cases over the 14 days was also a focus of the study.

Feature selection

First, we analyzed the findings regarding the correlations between the 44 features and the number of new confirmed COVID-19 cases (Table 1, Table S1). A higher importance value indicates the feature has more obvious relation to the number of new confirmed cases per million people. To avoid the influence of some special events or the imbalanced testing abilities between workdays and weekends, we smoothed the concrete number of new cases per day by using moving average over a 7-day period. The same goes for other features with smooth. If not specifically pointed out, all prediction results were also smoothed by a 10-day period to suppress noise and increase the accuracy30. Surprisingly, the features of group 3, ‘humidity’ and ‘temperature’, ranked in the top three (Table 1). From this perspective, it is very likely that the COVID-19 pandemic is closely related to environmental factors. The characteristics in group 1 that are directly related to the pandemic, such as ‘the number of new cases smoothed per million’ and ‘the number of new tests smoothed per thousand’ are ranked highly. Of the group 2 features, GDP ranks the highest. Policy responses (group 4) are ranked low overall, probably because the correlations between policies and new cases are not obvious, beyond the analysis capability of the gradient boosting machine (GBM) based feature selector.

Based on the feature selection, we selected features among the group 4 policy responses that produced an importance rating of more than 120. We named this group of features group 4*. Group 4* comprised ‘school closures’, ‘restrictions on gatherings’, ‘cancellation of public events’, and ‘workplace closures’. Features that were ranked above 28th were selected as group all* for further experiments (Table 1). The symbol * represented features that were given an importance rating above 120 and groups that comprised these features.

Table 1 The 44 features sorted according to importance.
Full size table

Confirmation of time steps in the LSTM model

Time step is the length of the input days and is a necessary parameter for the running of the LSTM model. Interval is the parameter deciding whether it is necessary or how long is needed to skip a few days to forecast the future data after the input time. To decide the epoch of the LSTM model, we conducted experiments on each input, interval and prediction portfolio with a validation set. To better use the policy responses, we used two combination of features with importance over 120 (groups 1 + 3 + 4*, all*).

The results turned out that as the interval between the input and prediction dates became longer, the prediction became less effective (Table S2, S3). However, when the same time interval was used, the performance was improved to different degrees as the duration covered by the input data increased. Our initial hypothesis to explain this was that the effect of policy changes on the epidemic was apparent only after a long period.

A comprehensive comparison of the three performance indices indicated that the portfolio 84/0/14 has the highest EVS and R2 score, and a moderate RMSE when using feature 1 + 3 + 4*, which was the best predicted result (Table S2). Portfolios 28/0/14 and 56/0/14 followed closely behind. Portfolio 84/0/14 also performed good in group all*, whose features were importance over 120 (Table S3). The trend in the interval aspect and the portfolios 56/0/14 and 84/0/14 had similar performances in all* (Table S3)

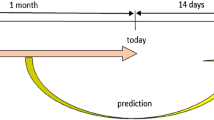
To be able to improve the exploration of the potential effects of policy responses on the COVID-19 pandemic, we prioritized the effect of a longer-period input time that was aimed at group 4, which was an 84/0/14 combination. Thus, based on the above analysis, 84 days was chosen as the time step inputted into the LSTM model combining with other parameters (Table S4).

Performance of different group combinations

The overall performance of different group combinations in this study is measured by explained variance scores (EVSs), R2 scores and root mean square errors (RMSEs). We used the median values of three evaluation methods to rank the overall predictions made by LSTM model of different group combinations. The top three accurate predictions are marked in the analysis of each validation sets (Table S5). With the combination of the performance results of 6 validation sets, we ranked the 11 group combinations (Table 2). The three groups with the best prediction results were Ì groups 1 + 3, 1 and 1 + 3 + 4*. The three groups with the worst results were groups 1 + 2 + 4, 1 + 4, and all.

Generally, the ranges of three evaluations were EVS (-285, 0.628), R2 score (-305, 0.526), RMSE (4281.3, 7021.8). The median values of EVS, R2 score and RMSE are 0.535, 0.35, and 5486.6. From different evaluation criteria, the maximum value of EVS reached 0.628, provided by group 1. The maximum value of the R2 score was 0.526, from the group combination 1 + 3 + 4*. The minimum value of RMSE was 4281, which came from group 1.

In most experiments, group 1 had a definite advantage in prediction because it contained data directly related to the COVID-19 pandemic. Despite that, groups 1 + 3 showed an elevated effect and ranked first among all group combinations because group 3 showed a high importance ranking during the feature screening phase. Group 2 showed less correlation in the feature selection stage, and therefore the effect of groups 1 + 2 was reduced. Similarly, the group combinations 1 + 2 + 4 and 1 + 3 + 4 showed poor effects.

After feature selection, group 4* retained four features: ‘school closures’, ‘restrictions on gatherings’, ‘cancellation of public events’, and ‘workplace closures’. This retention led to an improvement in the predictions that involved this group compared with those produced through the use of groups 1 + 4. According to the median values, the combination of 1 + 4* ranked better than that of 1 + 2, which showed that the policy responses played a role in the prediction of new COVID-19 cases. The performance values of the combination 1 + 3 + 4*, which ranked in third place, were close to those of groups 1 + 3. This result also indicated that policy responses selected from feature selection possessed higher importance in a few countries which may be an insight for further study.

Table 2 Overall group performance comparison of three evaluation methods by LSTM model.
Full size table

Prediction performance by different countries/regions

Although the model showed a reasonable level of prediction in general, due to the differences in the real situations and statistics for each country/region, some countries/regions showed good fits under certain feature combinations with the LSTM model, while prediction performances for other countries/regions were different from the overall results. Next, we examined the predictions for different countries/regions in this model when different validation sets were used (Table S6–S20).

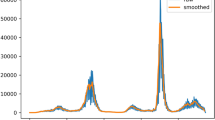
In our study, the most accurate predictions of new confirmed COVID-19 cases were for Germany, Italy, and the United States in all three metrics, while the worst performances were for Hong Kong, Sweden, and China (Table 3, Fig. 1). China and South Africa even showed R2 scores that were less than zero. Singapore showed the highest RMSE, of 11301, which did not quite match the fit state presented by its prediction result and was probably produced because the number of new cases there was higher than in other countries/regions.

Table 3 Performances of 15 countries/regions as predicted by the LSTM model.
Full size table
Figure 1
figure 1

Plots of real new cases, predicted new cases and smoothed predicted new cases for 15 countries. (A) Prediction chart of new cases in Hong Kong through the use of groups 1 + 3, validation set 5; (B) Prediction chart of new cases in China through the use of groups 1 + 2 + 3, validation set 2; (C) Prediction chart of new cases in United States through the use of groups 1 + 3 + 4, validation set 5; (D) Prediction chart of new cases in the United Kingdom through the use of group 1, validation set 3; (E) Prediction chart of new cases in Japan through use of groups 1 + 3 + 4*, validation set 2; (F) Prediction chart of new cases in Singapore through use of groups 1 + 3, validation set 5; (G) Prediction chart of new cases in Sweden through use of groups 1 + 3 + 4*, validation set 2; (H) Prediction chart of new cases in Australia through use of groups 1 + 4*, validation set 4; (I) Prediction chart of new cases in Israel of Group 1 + 2 + 3, Validation set 3; (J) Prediction chart of new cases in France through use of groups 1 + 3, validation set 5; (K) Prediction chart of new cases in South Korea through the use of groups 1 + 3, validation set; (L) Prediction chart of new cases in Italy through the use of groups 1 + 4*, validation set 1; (M) Prediction chart of new cases in Germany through the use of group 1, validation set 3; (N) Prediction chart of new cases in India through the use of groups 1 + 3 + 4,validation set 1; (O) Prediction chart of new cases in South Africa of through the use of group 1, validation set 1.

Full size image

Improvement of LSTM model

Based on the data from the existing model, we wondered whether some of our performance results were influenced by the insufficient ability of the LSTM model to generalize because of the specific pandemic controls of individual countries/regions. Thus, we suggested that the removal of individual countries/regions from datasets might improve the model’s overall performance.

The former results show that the three worst-performing countries/regions were Hong Kong, Sweden, and China (Table 3). For Hong Kong, the median values of two of the three evaluations, other than RMSE, were reasonable, and the prediction chart was close to the real fluctuations (Fig. 1A). For China, the median values of EVS and the R2 scores were negative, which indicated the inaccuracy of the prediction. However, the reported numbers of new COVID-19 cases in China were far fewer than those in other countries/regions, so its RMSE values would be small overall (Fig. 1B, Table S7). For Sweden, when its three evaluations and the prediction were combined (Fig. 1G, Table S12), the trend in the predicted number of new cases was generally close to the true value.

According to the above analysis, with all other conditions equal, we chose to remove China from the dataset to find out whether the overall effect of the LSTM model could be improved. China has the strictest control measures and very few cases, so it is reasonable to believe that the data in China did not share the same pattern as the data in other countries/regions, which may confuse the LSTM model.

After removing China from the dataset, the ranges of the three evaluations were: EVS, -35.7 to 0.678; R2 score, \(-\) 71.6 to 0.585; and RMSE, 4835.9 to 8037.4 (Table S21). Furthermore, the median values of EVS, R2 score and RMSE were 0.473, 0.278, and 5923.4. Compared with the prediction for 15 countries/regions (Table 2), the performances of all three evaluations declined to some extent. Different evaluation methods showed that the maximum value of EVS improved to 0.678, provided by group 1. The maximum value of the R2 score improved to 0.585, from the group combination of 1 + 3. The minimum value of RMSE increased to 4835.9, from groups 1 + 3. The top three performance portfolios were for groups 1 + 3, 1 and 1 + 3 + 4*, the same as the results for the 15 countries/regions.

From the above results, we found that the removal of the data for a country/region did not significantly improve or reduce the effectiveness of the LSTM model. Though some improvements occurred in the optimal value, the overall decrease in the effectiveness was expected because the number of poorer forecasts likewise increased. From these two experiments, we could conclude that the model’s overall prediction level and generalizability were stable and not drastically affected by some individual countries/regions.

Comparison of models

To illustrate the efficiency of the LSTM model, we used two other models, SVR and TCN with 84 input days and 14 prediction days, in the prediction experiment of 15 countries/regions (Table S22–S24). The group combination of 1 + 3 + 4* was chosen for the comparison because it offered better results when applied in the LSTM model.

It turned out that the LSTM produced overwhelmingly the highest values of the three evaluation methods (Table 4). The TCN model (Table S24) offered better fitting results than the SVR (Table S23), with higher EVS and R2 scores, due to its memory ability. The TCN model provided relatively high prediction for several countries under the metric of explained variance scores (EVS), including Germany (0.776), Singapore (0.741), and United Kingdom (0.698) (Table S24).

Table 4 Comparison of results from the three models through the use of Group 1 + 3 + 4*, Validation set 4 with 84 input days and 14 prediction days.
Full size table

Discussion

In this study, COVID-19-related data from 15 countries/regions are collected in order to investigate the role of different features in understanding the factors influencing new cases, with a focus on the potential role of policy responses to COVID-19. We collected multi-factor data and divided them into four major groups, which were: pandemic information, the basic information of countries/regions, climate, and policy responses. Then, through feature selection, we targeted 28 features that were most relevant to new cases development. To eliminate the instability of the results obtained from overfitting, we selected a continuous period of approximately 20 percent of the total period over which the data were collected for each country/region as the validation set. The validation set was arranged in such a way that it could be spread over the total time, the data in each day of at least one country/region appeared in the validation set. The main analysis step of this study was to determine which features were more influential in modeling the number of new confirmed cases of COVID-19, through the use of different feature group portfolios. The main model for the experiment was the LSTM and the main evaluation methods used were the EVS, R2 score and RMSE.

Regarding the overall performance of the group portfolio, groups 1 + 3, 1 and 1 + 3 + 4* produced the best three performances. It turned out that climate factors, namely temperature and humidity, have mainly influence the numbers of new cases apart from the direct pandemic statistics. We also find the positive role of specific policy responses, which were ‘school closures’, ‘restrictions on gatherings’, ‘cancellation of public events’, and ‘workplace closures’. Among the chosen 15 countries/regions, the prediction results for Germany, Italy and the United States fitted best with the reported figures, while the results for Hong Kong, Sweden and China fitted worst. Since Hong Kong and Mainland China have adopted the policy of dynamic zero COVID-19 strategy, trends of COVID-19 new cases are different from those of other countries using the same set of standard features, which makes it difficult for LSTM model to capture their internal pattern.

Then, this study decided to remove China from the training dataset and validate the generalizability of the model’s performance for the remaining countries/regions. The results showed that the performance results with the use of the LSTM did not change significantly due to the removal of one country. This finding may indicate the model’s stability and provided insight to apply the model to other country/region portfolios.

There were three novel aspects in this research. First, we added more features and types of features as predictors of new COVID-19 cases, such as policy responses, climate, and the basic information of the country/region and combined data from 14 countries/regions to predict the number of new confirmed COVID-19 cases in the remaining. Second, the input and prediction periods were extended to 84 days and 14 days respectively in this study, and the time span of the total data is around 900 which would be practical in general use and enabled the model to ‘learn’ more potential influences. Finally, this research compared the effect of the LSTM model with those of two other models. Although SVR has been used widely to compare DL models, the TCN method has only recently been used to make predictions related to COVID-19, there are few studies on it, and no scholars have compared it with LSTM.

During the collection of policy response data regarding COVID-19, we found it difficult fully to harmonize the rigor of policies across countries/regions. This was because certain countries/regions followed a zero COVID-19 policy, while others practiced herd immunity or aimed to minimize transmission. Therefore, although the level of rigor of policy response may be the same for different governments, the final achievement of pandemic prevention can be different due to various means of implementation. Therefore, the data collected were as objective as possible, but this objectivity did not consider the facts in each country.

Among the features that were collected for group 1 (pandemic information), R0 (the basic reproduction number) was related to the mathematical models of epidemic diseases. In this study, the value of R0 that we used was not calculated from the current number of people with the disease, but used a value commonly used in the existing literature. Also, the variation of the R0 value depended on when a new, endemic, mainstream variant appeared in the country/region. In addition, we did not combine other independent variables that are associated with the SIR/SEIR models with the currently available data, which may have led to some deviation from the true dissemination.

Conclusion

In this study, we collected a large amount of data related to COVID-19 and investigated the role of different features in understanding the factors influencing the total numbers of new confirmed COVID-19 cases over the subsequent two weeks. Our findings indicated that the combination of climate factors and pandemic information provided valuable insights into the dynamics of case numbers. Policy responses and the strengths of countries/regions also showed notable effects in certain countries (Italy, India, Japan, Sweden). The results of feature selection highlighted the importance of current measures, suggesting that some countries could benefit from streamlining existing policies and focusing on higher-priority interventions such as school closures or restrictions on gatherings. We also verified that the LSTM model effectively captured temporal dependencies and performed better than SVR and TCN models in modeling the observed data. Overall, these analyses enhanced our understanding of the factors affecting COVID-19 case numbers and may inform public health strategies in other countries/regions, especially when using a wider variety of features and data collected over a longer period.

Methods

Data for Covid-19

Data collection

We collected data related to COVID-19 for a total of 15 countries/regions. The data we collected was divided into four groups: pandemic information, the strength of countries/regions in terms of financial situation and level of development, climate, and policy responses.

Group 1 contained direct pandemic statistics, which comprised the various values that were associated with the COVID-19 outbreak in the country and which were collected also by researchers worldwide who contribute to the website ‘our world in data’31. Features in this group were numbers of: new cases smoothed, new cases smoothed per million, new deaths smoothed per million, total tests, total tests per thousand, new tests smoothed, new tests smoothed per thousand, total vaccinations, people vaccinated, people fully vaccinated, total boosters, new vaccinations smoothed, total vaccinations per hundred, people vaccinated per hundred, people fully vaccinated per hundred, total boosters per hundred, new vaccinations smoothed per million, newly vaccinated people smoothed and newly vaccinated people smoothed per hundred. ‘Smoothed’ means we used the mean in a 7-day period to replace the original value to suppress mutation points. To demonstrate the contagious power of virus variants, we also had the statistics on the specific variants that were widely disseminated across the world, which were the original, alpha, beta, delta, and omicron. The basic reproduction number (R0) for each virulent strain was listed as original (2.2), alpha(4.5), beta (4.5), delta (5.1), and omicron (8).

Group 2 comprised data on countries’ strengths, which mainly represented the basic economic situation and its potential to defend the population against COVID-19. Group 2 contained gross domestic product (GDP) per capita, life expectancy, the region’s human development index and population.

Group 3 contained data on climate, which comprised average temperature and humidity data. It was difficult to assign a specific climate value to countries of huge geographical areas. Therefore, we selected the climate information for cities that reported high numbers of cases or that were representative of several countries (Table 5).

Group 4 included all the policy responses made by 15 countries/regions. We selected 12 measures: international travel controls, restrictions on internal movements, closed public transport, a testing policy, contact tracing, a vaccination policy, use of face coverings, stay-at-home requirements, cancellation of public events, restrictions on gatherings, workplace closures and school closures. Most data regarding policy responses were taken from the website of ‘our world in data’. In a small number of cases, to confirm the details of policies, we also visited the corresponding country/region’s news website32,33.

Our data period was from January 2020 to June 2022,  900 days in total. January 2020 was chosen because, in this month, most countries/regions except China reported their first case of COVID-19.

Table 5 Representative cities in group 3 climate.
Full size table

Data preprocessing

To eliminate the influence of orders of magnitude of different features, the features are min-max normalized, so the range of each feature would be limited to the range zero to one. After the prediction had been made, the results would return to the original order of magnitude through inverse transformation.

Next, we explored features that were correlated the least with the number of new confirmed cases through the application of a gradient boosting machine (GBM) based feature selector, which can give as some preliminary hints about the useful features.

Prediction process

We used data from a period of 84 days to predict the total number of new confirmed cases that would occur in the following 14 days. To evaluate each model more comprehensively, we used the data from 14 countries/regions to train a model and then to test it in the 15th country/region (testing set). We repeated this step 15 times to test the model in each of the 15 areas. For each of the training country/region, the data in a period of  20 percent time span was randomly selected to consist of the validation set, i.e., 150 days of data. It rolled over the whole dataset to ensure it could spread over the total time, and the period that corresponded to the validation set was different for each country/region. The role of the validation set was to establish a criterion by which to stop the epoch of the training set and avoid overfitting. Therefore, the mixed data of 14 countries/coutries after excluding the validation set were the training set. To eliminate the uncertainty caused by the randomness of the validation set, we randomly selected six partitions of training/validation sets to see the overall effect of different groups on the prediction of new cases with the portfolio of 84/0/14 by LSTM.

After we had finished training and achieve the predictions, we smoothed the data obtained from the predictions. Then, the performance of each model’s parameters was evaluated, and the performance of 15 models was averaged to discover the generalized effect of this model. To obtain a composite score for each group portfolio in each validation set, we averaged the performance results for 15 countries/regions and combined the six randomly selected validation sets to obtain the overall performance.

Finally, we repeated the procedures on another two models and compared the performance of the three models. The whole procedure is exhibited in Fig. 2.

Figure 2
figure 2

Experimental procedure. Data from 15 countries and a total of 44 features were collected from date January 2020 to June 2022. Features were categorized into four groups, including pandemic information, countries’ strengths, climate, and policy responses. Features with high importance were selected for further experiments. Data from 14 countries/regions were used to train a model and then to test it in the remaining. The data from the 14 countries/regions were separated randomly into training and validation data. With regression algorithms, the trained models were used in the test data for prediction. Performances of different models and different feature combinations were evaluated.

Full size image

Design model for Covid-19 prediction

Three models were established to predict the number of new COVID-19 cases. To achieve a global comparison among different kinds of ML models, we select support vector regressor (SVR), temporal convolutional network (TCN) and long short-term memory (LSTM) as the representative of non-deep models, convolutional neural networks (CNNs) and recurrent neural networks (RNNs) respectively, which are three mainstream ML model categories. SVR is one of the most popular non-deep ML models, which can often perform well for different applications. TCN is a recently proposed CNN-based model with a long memory, thus more suitable for data in sequences compared with a vanilla CNN. As for LSTM, it is one of the most widely used model for data in sequences, it is better to find the long-term dependencies compared a vanilla RNN because of its strategies of “remember” and “forget”.

Support vector regression (SVR)

SVR was proposed as a variant of support vector machines (SVM), in which the output can be continuous (the output of SVM is discrete)34. Both SVM and SVR minimize the marginal error, the former is to maximize the margin of the hyperplane and the sample point closest to it (Fig. 3a), while the SVR is the opposite of SVM (Fig. 3b).

Mathematical formulas for the multidimensional data used by SVR are shown in Eq. (1), in which \(W_{i}\) and \(X_{i}\) are the input feature weights and values, b is bias, and y is the result under the parameters for true value or further calculations. M is the total number of samples in the dataset.

$$\begin{aligned} y=f(X)= {\textstyle \sum \limits _{i=1}^{M}} W_{i}X_{i}+b \end{aligned}$$
(1)

Equation (2) reflects the original optimization objective of the SVR, and ||W|| represents the magnitude of the vector. The sample points lie within the boundary and must satisfy Eq. (3), in which \(\varepsilon\) is the vertical distance within the interval zone (r) made by the model, also called the tolerance deviation.

$$\begin{aligned} \min _{w,b} \frac{1}{2} \left| \left| W \right| \right| ^{2} \end{aligned}$$
(2)
$$\begin{aligned} \left| y_{i}-(wx_{i}+b) \right| \le \varepsilon \end{aligned}$$
(3)

Equations (2) and (3) are used to determine the parameters w and b. The SVR model is set to maximize r and to minimize loss, which depends on the C parameter (Eq.4).

$$\begin{aligned} loss=C {\textstyle \sum \limits_{i=1}^{M}}l_{\varepsilon }(f(x_{i},y_{i})) \end{aligned}$$
(4)

Since in a realistic situation, it is difficult to guarantee that all data will fall in the interval bands, slack variables \(\xi _{i}\) and \(\xi _{i}^{*}\) are added to establish a loss function. The former slack variable \(\xi _{i}\) is used when samples fall above r, and the latter is used in the opposite case, so some samples are excluded. Overall, when all the constraints are combined, the ultimate optimization objective of the SVR is calculated as followed:

$$\begin{aligned} \begin{aligned} \min _{w,b,\xi _{i},\xi _{i}^{*} } \frac{1}{2} \left| \left| W \right| \right| ^{2} +C {\textstyle \sum _{i=1}^{M}}(\xi _{i},\xi _{i}^{*}) \\ s.t.f(x_{i} )-y_{i} \le \varepsilon +\xi _{i} \\ y_{i} - s.t.f(x_{i} ) \le \varepsilon +\xi _{i} ^{*} \\ \xi _{i} \ge 0,\xi _{i} ^{*} \ge 0,i=1,2,...M \end{aligned} \end{aligned}$$
(5)

After constraints are solved, we can obtain Lagrangian multipliers that are non-negative real numbers. Then, kernel functions are employed for non-separable classes. This provides the possibility of non-linear operations and accommodates fast operations in high-dimensional feature spaces. Finally, the SVR function is mathematically obtained (Eq. 6).

$$\begin{aligned} f(x)=\sum _{i=1}^{M}(a_{i}^{*}-a_{i}) \kappa (x_{i},x)+b \end{aligned}$$
(6)

With the use of the kernel function (Eq. 7), more kernel types can be used in realistic datasets, such as the radial basis function (RBF), polynomial (Eq. 8) and Gauss (Eq. 9) kernels, in which \(\sigma\) and d are the parameters of the kernel used to tune. Results can be improved by optimizing these parameters35. In our experiments, we applied RBF kernel.

$$\begin{aligned} \kappa (x_{i},x)= & \varphi (x_{i}),\varphi (x) \end{aligned}$$
(7)
$$\begin{aligned} \kappa (x_{i},x_{j})= & (x_{i}^{T} x_{j})^d \end{aligned}$$
(8)
$$\begin{aligned} \kappa (x_{i},x_{j})= & exp(-\frac{\left\| x_{i}-x_{j} \right\| ^2 }{2\sigma ^{2} } ) \end{aligned}$$
(9)

Temporal convolutional network (TCN)

The TCN is a model developed from the CNN. Although CNNs are usually associated with tasks that use two-dimensional data, such as image recognition, compared with other DL structures in existing studies, they have proved useful in sequence modelling and prediction since the TCN was proposed36.

The CNNs consist of three kinds of layers: the convolutional, max pooling and fully connected layers. When the convolutional layer encounters data, it extracts specific features based on local patterns. The max pooling layer ignores some useless information while it keeps the crucial ones to enable training with fewer parameters. The fully connected layer makes classification or regression judgements with features and parameters.

With the characteristics of a vanilla CNN, a TCN can extract features in a cross-time step. To achieve similar functionality to an RNN, a TCN must solve two problems. One is to guarantee the exact time step of both input and output figures. The other is to guarantee that time series data do not leak, which means that data that follow the time series of the data being processed or outputted cannot be input into the next layer. Thus, one-dimensional convolutional layers and causal convolutions have been induced in TCN models.

Then, to solve the problem that the convolution layer is too deep if the time series is too long, dilated causal convolutions have been induced (Fig. 3c), in which the kernel size is a stable number but the receptive field, namely the local range can be “seen” by the kernel, is enlarged by skip one or multiple points. When dilation factor, which usually is the exponential power of two, is employed, some information is excluded to improve the completion efficiency of the model. A residual block can be used also to strengthen the generic ability of the structure and to avoid the vanishing of gradients after dilation.

Long short-term memory (LSTM)

The RNN is a common DL model that is commonly used to process sequence-type data. Although RNNs can deal with long sequences, they have limited long memory cycles and problems with vanishing gradients37. The evolution of an RNN, the LSTM cell, uses input, output, and forget gates to control the transmission of sequence information, which thus enables the preservation and transmission of a more extensive range of information (Fig. 3d).

The forget gate is a sigmoid function whose inputs are the output of the previous output \(h^{(t-1)}\) and the current input \(x^{(t)}\). It is used mainly to control the effect of past cell state \(c^{(t-1)}\) on the current memory unit state value \(c^{(t)}\), which can be described by:

$$\begin{aligned} f^{(t)}=\sigma (x^{(t)}W_{xf}+h^{(t-1)}W_{hf}+b_f) \end{aligned}$$
(10)

After new data are input into the block, the input gate and the candidate memory cell \(\tilde{c}^{(t)}\) jointly determine the degree to which the new memory content is added to the memory cell, which can be displayed as:

$$\begin{aligned} i^{(t)}= & \sigma (x^{(t)}W_{xi}+h^{(t-1)}W_{hi}+b_i) \end{aligned}$$
(11)
$$\begin{aligned} \tilde{c}^{(t)}= & \tan h(x^{(t)}W_{xc} +h^{(t-1)}W_{hc}+b_{c}) \end{aligned}$$
(12)

With the previous self-state \(c^{(t-1)}\) processed by forget gate and the value of \(\tilde{c}^{(t)}\) modulated by input gate, the current core junction of LSTM cell, \(c^{(t)}\) is obtained, which is given by:

$$\begin{aligned} c^{(t)}=f^{(t)} \odot c^{(t-1)}+i^{(t)}\odot \tilde{c}^{(t)} \end{aligned}$$
(13)

The output gate \(o^{(t)}\) controls the filtering extent of the cell state \(c^{(t)}\), which will be then divided into the output result \(Y^{(t)}\) and the hidden state \(h^{(t)}\). Moreover, \(c^{(t)}\) and \(h^{(t)}\) will be delivered into next memory unit for further calculation. Detailed formulations are showed below:

$$\begin{aligned} o^{(t)}= & \sigma (x^{(t)}W_{xo}+h^{(t-1)}W_{ho}+b_i) \end{aligned}$$
(14)
$$\begin{aligned} h^{(t)}= & o^{(t)} \odot \tan h(c^{(t)}) \end{aligned}$$
(15)

To ensure that \(h^{(t)}\) is always between \(-\) 1 and + 1, the hidden state vector has a gated version of a hyperbolic tangent of the memory cell. When the value of the output gate \(o^{(t)}\) is close to 1, the information is passed from the memory to the predictor, while when the \(o^{(t)}\) value is close to 0, all the information is kept in the memory cell without further processing.

Figure 3
figure 3

Simplified schematic diagram of the used model. (A) SVM; (B) SVR; (C) Simple diagram of dilated causal convolutions, kernel size= 2, dilations= [1,2,4,8]; (D) Block diagram of LSTM cell.

Full size image

Performance evaluation

We combined several evaluation methods to reflect the prediction effects of different models and different cases38. C represents ground-truth value and \(\hat{C}\) is the predicted value.

The Root Mean Square Error (RMSE) is used to measure the deviation between the observed value and the true value (Eq. 16). Less RMSE means the rooted mean squared difference between the predicted result and the ground-truth value is closer, namely the performance is better.

$$\begin{aligned} RMSE = \sqrt{\frac{ {\textstyle \sum _{i=1}^{M}(C-\hat{C})^2}}{M} } \end{aligned}$$
(16)

The explained variance score (EVS) is used to measure the degree to which the model explains the fluctuations of the dataset (Eq. 17), and its value takes the range [0,1]. The closer it is to 1, the more closely the independent variable explains the variance variation of the dependent variable, and the closer it is to 0, the worse the effect.

$$\begin{aligned} EVS=1-\frac{Var\left\{ C-\hat{C} \right\} }{Var\left\{ C\right\} } \end{aligned}$$
(17)

R2 score is the coefficient of determination, reflects the proportion of the total variation in the dependent variable that can be explained by the independent variable through the regression relationship. Value of R2 score takes the range [0,1], the expected value is 1 for the best model and is expressed mathematically (Eq. 18).

When R2 = 1, the predicted and true values in the sample are exactly equal without any error. This finding indicates that the independent variable explains exactly the dependent variable in the regression analysis. When R2 = 0, the numerator equals the denominator and each predicted value in the sample is equal to the mean value.

The R2 score is not the square of R and may be negative (var >RMSE), which means that the model is less accurate than when the mean is calculated.

$$\begin{aligned} R^2=1-\frac{RMSE}{Var}=1-\frac{ {\textstyle \sum _{i=1}^{n}}(C-\hat{C})^2 }{{\textstyle \sum _{i=1}^{n}}(C-C^2)^2} \end{aligned}$$
(18)