1 Introduction

The outbreak of coronavirus disease 2019 (COVID-19) led to a global epidemic [1]. The World Health Organization (WHO) declared the outbreak as a Public Health Emergency of International Concern and subsequently a pandemic [2]. Several countries introduced tough measures including lockdown of borders and major cities, social distancing, and isolation of the infected population. All these efforts were aimed at controlling the spread of this highly infectious virus and thereby to reduce severe illness in humans. However, it is still unclear what role these intervention policies have played in controlling the spread of the epidemic.

On March 27, 2020, at the time of writing this paper, 4 months after the “first” case was reported (December 8, 2019) [3], 81,394 infected cases had been confirmed in mainland China with 3295 reported deaths. Of these, 61.4% of the infections and 77.1% of the deaths had occurred in Wuhan [4], the initiating center of this outbreak. Globally, the USA, Italy, Spain, Germany, France, Iran, UK, and Switzerland now each have more than 10,000 confirmed cases [5].

Recent studies have shown that human mobility plays a key role in the spread of epidemics [6,7,8,9,10,11,12]. Specifically, epidemic spread in urban networks can be regarded as a reaction–diffusion process in which local reaction occurs within cities, and city-wide diffusion is driven by the human mobility across those cities [13]. However, most conventional epidemic spread models (e.g., susceptible–infected–recovered, SIR) [14] cannot fully account for the diffusion dynamics caused by mobility, which are extremely important in highly connected urban networks. The situation in Wuhan also highlighted the role of human mobility in spreading and controlling COVID-19. As a central transportation hub, Wuhan has direct links to its surrounding cities and most of the major cities in other parts of China (Fig. 1a), which made the epidemic quickly spread to China through the urban transportation networks. In order to control the spread of the epidemic, Wuhan has been “locked down” since January 23, 2020 [15], and strictly controls population movement (Fig. 1b). In terms of infected cases, the lockdown of the city has achieved remarkable results, with fewer than 100 new cases reported daily in Wuhan since March 6, 2020 (the population of Wuhan is over 10 million) [16].

Fig. 1
figure 1

Population flow and the cumulative number of confirmed cases. a Population flow from Wuhan to other cities of China as of January, 2020. b Outflow index of Wuhan from January 1, 2020, to February 7, 2020. The quarantine policy was implemented on January 23, 2020. The outflow dropped dramatically after that day. The dataset to calculate population flow is detailed in Methods. c, d The number of cumulative confirmed cases of four cities from R dataset in Hubei and five main cities (see Sect. 2)

Full size image

Right now, policy makers in all countries are facing unprecedented challenges in making decisions on when and what degrees of intervention measures should be implemented to tackle the pandemic. Meanwhile, a large number of publications provide medical and policy support from different perspectives [17]. The biological, clinical [18,19,20,21], and spreading characteristics of the virus [3, 22, 23] have been extensively discussed, and several modeling-based studies have addressed the spread of the virus through human migration [24,25,26], and different measure policies. Literatures [27,28,29,30] review the modeling frameworks on general disease dynamics and COVID-19 virus transmission. However, few have modeled the effect of intervention timing and its strength on controlling the spread of the epidemic [31,32,33,34].

Here, by using a nationwide human movement dataset, we developed a networked meta-population model to estimate the spread of COVID-19 across 371 prefectural-level cities in mainland China under different intervention scenarios. We found that both the time of initiating an intervention and its effectiveness had a very large impact on controlling the epidemic. Under the least effective scenario, i.e., doing nothing, we estimated that the virus would have infected over one billion people, approximately 85% of the Chinese population. By implementing a tough intervention as imposed in Wuhan (city-wide quarantine, strictest travel ban, minimized social contact, widespread testing and isolation, etc.), the spread was reduced substantially, and the cumulative infected population in China was modeled to be 0.28 million (95% CI 0.178–0.604) in 7 months, 0.02% of 1.18 billion with no intervention. If the time of the intervention had been brought forward by ten days, the estimated number of infected cases for the same period would be 65,200 (95% CI 4100–13,900), which was a quarter of the tough intervention case. For a less effective intervention, the model estimated a tenfold increase in infected cases and deaths, but even here if it was implemented earlier, the number of the cases would reduce substantially.

2 Methods

2.1 Data

2.1.1 Population migration dataset

The city-level mobility network is constructed from the Baidu Migration Project [35]. This dataset is calculated based on the movement of mobile phones using Baidu location-based services. It includes two parts: (1) a daily origin–destination matrix recording the migration percentage \(P_{ij}^{t}\) of the top 100 inflow and outflow cities for 371 prefecture-level cities in China. The total population of these cities is 1.39 billion, accounting for over 99% of the national population. \(P_{ij}^{t}\) denotes the proportion of migration from the city \(j\) to \(i\), to the total population that moved out from the city \(j\) in day \(t\); and (2) a flux index \(F_{j}^{t}\) of the daily inflow and outflow for each city \(j\) in day \(t\). This index is proportional to the number of mobile phone users who migrate into or out of a certain city (Fig. 1a, b). Both parts cover movements between January 1, 2020, and February 7, 2020. To alleviate the fluctuation of \(P_{ij}^{t}\), an “average” mobility matrix P over the whole period is derived, where \(P_{ij} = \Sigma_{t} \left( {P_{ij}^{t} F_{j}^{t} } \right)/\Sigma_{t} F_{j}^{t}\).

2.1.2 Case dataset

We collected city-level reported case data from the R package nCov2019 [36], which includes the cumulative number of confirmed, dead, and recovered individuals each day in each city (Fig. 1c, d). To estimate the parameters of our model, such as incubation time, we also used individual case data derived from the Wolfram database [37]. The original sources of these case data are from the National Health Commission, local health commissions, and Chinese Centers for Disease Control and Prevention [38]. We supplemented the cumulative confirmed case data before January 10, 2020 (the start date of the case dataset provided by the R package) with cases reported by Li et al. [3].

2.2 Model

2.2.1 The networked meta-population model

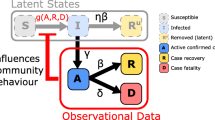
We extended the classic SIR model [39] by introducing two new health states, i.e., unconfirmed cases and death, as well as taking into account inter-city human mobility [9]. In our model, health states were defined by susceptible, unconfirmed infectious, confirmed, recovered, and dead (SICRD model). The setting of the five-state model reflects the real-life situation in which an infectious person may recover or die before receiving a formal diagnosis (unconfirmed cases). The model structure and the transition among the five states are illustrated in Fig. 2a.

Fig. 2
figure 2

Schematic of the SICRD model, the initial conditions, and timeline of the simulation. a Model schematic and initial conditions. \(S_{n}\), \(I_{n}\), \(C_{n}\), \(D_{n}\), and \(R_{n}\) are the populations of the states, and \(s_{n}\), \(i_{n}\), \(c_{n}\), \(d_{n}\), and \(r_{n}\) are the relative fractions of the states, respectively, which can be easily calculated by dividing S, I, C, D, and R with the city's population. The explanation of model parameters is listed in Table 1. As the initial condition for Wuhan, the value of the I state is estimated by fitting the case data (see SI Section 2). The number of confirmed cases, C = 57, is based on Li et al. [3]. S, the initial susceptible number, is assumed to be the city population size, which is collected from city population data (https://www.citypopulation.de/). b The timeline of the simulation

Full size image

Specifically, health states were defined as follows:

  • Susceptible state: healthy individual without COVID-19; a person in this state can be infected if they contact an infectious person.

  • Unconfirmed infectious state: persons in this state can be symptomatic or asymptomatic but they are infectious. A person in this state can stay in the same state, or move to a confirmed state, recovered state, or dead state.

  • Confirmed state: those with viral confirmation. We have assumed that a person in this state will be isolated; therefore, he/she will have no chance to infect other people. A person in a confirmed state can stay in the same state or move to recovered or dead states.

  • Recovered state: those who are cured and immune. We have assumed that a person in this state would not be infectious or be infected again.

  • Death state: the deaths due to COVID-19

To be noticed that, our model is different from the traditional SEIR model (susceptible, exposed, infectious, and recovered). The people in the unconfirmed infectious state contain the exposed state in the conventional SEIR model. While in our model, we assume that the infected cases are infectious immediately.

Mathematically, the model is defined by the following equations [see Supplementary Information (SI) Section 1 for the derivation]:

$$ \begin{aligned} \frac{{\partial s_{n} }}{\partial t} & = - \frac{{R_{0} }}{{T_{L} }} s_{n} i_{n} + \omega \mathop \sum \limits_{m \ne n}^{{}} P_{mn} \left( {s_{m} - s_{n} } \right) \\ \frac{{\partial i_{n} }}{\partial t} & = \frac{{R_{0} }}{{T_{L} }} s_{n} i_{n} - \frac{\alpha }{{T_{L} }} i_{n} - \frac{1 - \alpha }{{T_{L} }} i_{n} + \omega \mathop \sum \limits_{m \ne n}^{{}} P_{mn} \left( {i_{m} - i_{n} } \right) \\ \frac{{\partial c_{n} }}{\partial t} & = \frac{\alpha }{{T_{L} }} i_{n} - \frac{1}{{T_{R} }} c_{n} \\ \frac{{\partial d_{n} }}{\partial t} & = \frac{{\beta \left( {1 - \alpha } \right)}}{{T_{L} }} i_{n} + \frac{\beta }{{T_{R} }} c_{n} \\ \frac{{\partial r_{n} }}{\partial t} & = \frac{{\left( {1 - \beta } \right)\left( {1 - \alpha } \right)}}{{T_{L} }} i_{n} + \frac{1 - \beta }{{T_{R} }} c_{n} + \omega \mathop \sum \limits_{m \ne n}^{{}} P_{mn} \left( {r_{m} - r_{n} } \right) \\ \end{aligned} $$
(1)

where \(s_{n} = S_{n} / N_{n} , i_{n } = I_{n} / N_{n} , c_{n} = C_{n} / N_{n} , r_{n} = R_{n} / N_{n} , d_{n } = D_{n} / N_{n}\) are the fractions of susceptible, unconfirmed infectious, confirmed, recovered, and dead individuals in city n, respectively, and \(N_{n}\) is the population size of city n. P is the mobility matrix calculated based on the migration data (see Sect. 2), and \(0 \le P_{mn} \le 1\) denotes the proportion of migration from city n to the city m, to the total population who left city n. Infectious people could move to other cities to induce epidemic outbreaks in other cities. The initial states are listed in Fig. 2a.

Detailed descriptions and estimation of parameters \(R_{0}\), \(T_{L}\), \(T_{R}\), \(\alpha\), \(\beta\), \(\omega\), and \(I_{{{\text{wuhan}}}} \left( 0 \right)\) are shown in Table 1 and SI Section 2. \(T_{L}\), \(T_{R}\), and \(\beta\) can be estimated from patient clinical records, and \(\omega\) can be estimated based on the Baidu migration dataset, which is calculated based on the movement of mobile phone users (see Sect. 2). The remaining three free parameters \(R_{0}\), \(\alpha\), and \(I_{{{\text{wuhan}}}} \left( 0 \right)\) need to be estimated with reported city-level case data by fitting the number of confirmed cases for all Chinese cities before February 7, 2020, in order to minimize the loss function: \(\mathop {\min }\limits_{{R_{0} , I_{{{\text{wuhan}}}} \left( 0 \right), \alpha }} L = \mathop \sum \nolimits_{n}^{{}} \mathop \sum \nolimits_{t}^{{}} \left[ {\log_{10} \left( {c_{n} \left( t \right)N_{n} } \right) - \log_{10} \left( {C_{n}^{*} \left( t \right)} \right)} \right]^{2} \quad \left( {{\text{see}}\;{\text{Methods}}\;{\text{and}}\;{\text{SI}}\;{\text{section}}\;2} \right).\)

Table 1 Parameters of the SICRD model. We report the median values of \(R_{0}\), \(\alpha\), and \(I_{{{\text{wuhan}}}} \left( 0 \right)\) and mean values of \(T_{L}\), \(T_{R}\), and \(\omega\) with 95% CIs
Full size table

To solve this optimization problem, we use the differentiable ODE solver implemented by the framework of PyTorch [41]. The model and the estimated parameters are robust to changes in other parameters (SI Section 2). All the following results and the confidence intervals (CIs) are obtained after 360 repeated experiments (Table 1).

2.2.2 Intervention and relaxation

Further, we introduce an intervention term to simulate the intervention strategy that the Chinese government implemented to reduce contact or interaction among the population. By leaving all the equations and parameters unchanged in Eq. (1), we altered the model by multiplying \(\xi\) to the infectious term, i.e., \(s_{n} i_{n}\) in the first and the second lines of Eq. (1), such that:

$$ \xi \left( {t,{ }t_{0} ,t^{*} ,\lambda } \right){ } = 1/\left[ {1{ } + {\text{ e}}^{{\lambda \left( {t - t_{0} } \right) - {\ln}\left( {1/\epsilon - 1} \right)}} { }\left] {{ } + 1/} \right[1{ } + {\text{ e}}^{{\lambda \left( {2t{*} - t - t_{0} } \right) - {\ln}\left( {1/\epsilon - 1} \right)}} { }} \right]{ }. $$
(2)

There are three key parameters to describe the intervention term \(\xi\): (1) The initiating time \(t_{0}\) captures the time when the government started to apply intervention policies (e.g., traffic control, social distancing, and quarantine patients). (2) \(\lambda\) models the rate at which the intervention can take effect to reduce the reproduction number from \(R_{0}\) to \(\epsilon R_{0}\); a larger value means the spread can be reduced in a shorter time. \(\epsilon\) is the ratio of an acceptable reproduction number that can control the spread of the virus. (3) The timing \(t^{*}\) when we can relax the intervention. Overall, the term \(\xi\) models the temporal and effective dimensions of an intervention that governments use to prevent the epidemic spreading. The functional form of Eq. (2) is shown in Fig. 3. The values of \(t_{0}\), \(\lambda\), \( t^{*}\), and \(\epsilon\) are presented in Table 2.

Fig. 3
figure 3

The functional form of the intervention and relaxation term when \(t^{*} < \infty\). The two terms in Eq. (2) are symmetric along the axis \(t = t^{*}\). That is, we assume that the relaxation process reverses the intervention process. When \(t < t^{*}\), \(\xi\) decays as an S-shaped function of \(t\) because any policy needs time to implement, while \(\xi\) grows in an S-shaped curve when \(t > t^{*}\), and this simulates the slow relaxation of intervention. The detailed illustration of Eq. (2) can be read in SI Section 3

Full size image
Table 2 Parameters of the intervention and relaxation terms in SICRD model
Full size table

3 Results

3.1 Model validation

We validated the model by comparing the results estimated from the model under the actual scenario (the definition of different scenarios is detailed below) with the observed cases reported in China. Figure 4 compares the model-predicted confirmed cases with the reported confirmed cases at the national level. The model predicted well beyond the time period for parameter estimation, which demonstrates the validity of our model. However, we notice that since February 7, the model and actual data have deviated in individual cities (Table S4). This is likely to be due to the fact that Wuhan has changed the diagnosis criteria to include all clinical confirmed cases, while the rest of the cities still used the same diagnoses tool as before. The details of error analysis can be referred to SI Section 3.3.

Fig. 4
figure 4

Model validation. The x-axis is the time starting from January 1, 2020, in days. The confirmed cases (lines with dots) predicted by the model fit the reported case data (circles) well, indicating the effectiveness of our model and parameters

Full size image

Our model can also predict the number of “real” infected people (confirmed + unconfirmed infectious), as shown by the straight lines in Fig. 4. The results show that the real situation was likely to be much more serious than the reported data for all cities, especially those in Hubei Province. For example, our model predicted that the total number of infectious (confirmed + unconfirmed infectious) cases in Wuhan was more than three times than the confirmed number at most time points, and seven times higher at the beginning of the epidemic [155 reported cases and 1140 (95% CI 760–1680) model-predicted cases, as of January 7, 2020]. The large gap between the numbers of confirmed and infected cases in Wuhan was documented in a recent study [42]. This reflects the fact that a large number of infectious people could not obtain any appropriate treatment due to the limited medical resources in Wuhan, and/or they had only mild symptoms or were even asymptomatic.

3.2 Scenario analysis

We ran the model for 200 days (from January 1, 2020, to July 18, 2020). We will discuss the simulation results under five scenarios: (1) base case scenario: without intervention; (2) actual scenario: with intervention started from January 23, 2020, and reduced the reproduction number to \({\epsilon R}_{0}=0.002\) within five weeks; (3) early action scenario: same as the actual scenario but the intervention was implemented ten days earlier; (4) less effective scenario: same as the actual scenario but weaker intervention strength; and (5) early action but less effective scenario: same as the early action scenario but weaker intervention strength.

3.3 Base case scenario (without intervention)

According to our estimation, 1640 (95% CI 1220–1910) infectious cases were exported from Wuhan to all over the country before January 23, 2020, when the city-wide quarantine intervention policy was implemented.

The dynamics of some representative cities are shown in Fig. 5. There are two key findings. First, there would be two peaks in the spread of the disease (Fig. 5). The first peak would be the cities in Hubei Province, e.g., Wuhan, Xiaogan, and Huanggang. The second peak would be large cities such as Guangzhou. In those cities, this peak would be delayed by approximately three to four weeks compared with Wuhan. Second, the city with the most infections would be Chongqing (not Wuhan) because Chongqing has the largest population in China. Several other large cities (e.g., Beijing, Shanghai, and Guangzhou) would have more infections than Wuhan. The cumulative number of infectious cases for mainland China would be 1.18 billion (95% CI 1.16–1.22), accounting for 85% of the population of China.

Fig. 5
figure 5

Basic case scenario without any intervention. The y-axis is the existing confirmed and infected populations

Full size image

3.4 Actual scenario (\(t_{0} = 22, \;\lambda = 0.4, \;t^{*} \to \infty\))

The Chinese government implemented strong intervention policies to prevent the spread of the epidemic. For example, most cities in Hubei Province closed their inter-city transportation and implemented strict control over intra-city traffic. Schools and factories were closed, and only few daily necessities stores were allowed to open. Therefore, to derive better simulation results, we incorporated these interventions into the model as shown in Eq. (2).

Our model shows that if interventions could significantly reduce the reproduction number to \(\epsilon R_{0} = 0.002\) in a short time window (~ 35 days, \(\lambda = 0.4\)) after the outbreak, which was close to the real situation in China, the peaks of the infected individuals of Wuhan, Huanggang, Chongqing, and Shanghai would reach 48,000 (95% CI 22,300–176,100), 12,600 (10,600–14,800), 1770 (1430–220), and 1770 (1430–2250), respectively (Fig. 6a, b) and the cumulative infected population for the whole simulation period would be approximately 284,000 (178,000–604,000) for the entire country, approximately 0.02% of the base case scenario.

Fig. 6
figure 6

Epidemic predictions under different scenarios of policy intervention. The actual (a, b), early action (c, d), less effective (e, f), and early but less effective scenarios (g, h) for four cities in Hubei Province and five main cities of China. The y-axis is the existing median confirmed or infected populations. i, j The phase diagram of the cumulative number of confirmed (i) and death (j) cases under different intervention starting dates \(t_{0}\) and strengths \(\lambda\)

Full size image

The predicted trend of the epidemic fits well with the latest data, with the predicted curves peaking in mid-February (Fig. 6a, b). However, cities may have different behaviors due to the variation in intervention strength, which cannot be reflected in our model because all the modeled parameters were shared among all cities.

The model predicted that a total of 6500 (95% CI 4100–13,900) people would die as a result of COVID-19 in China out of 284,000 infected cases. In fact, as treatment levels continue to improve, the fatality rate may decrease, and the corresponding total number of deaths may also fall below this predicted value.

3.5 Early action scenario (\(t_{0} = 12, \;\lambda = 0.4,\; t^{*} \to \infty\))

In this scenario, we assumed that the government implemented a strict intervention policy ten days before the actual date, i.e., January 13, 2020 (\(t_{0} = 12\)), while the control intensity is the same as in the previous scenario (\(\lambda = 0.4\)). The simulation shows that the infected population would still reach a large number of people (14,000, 95% CI 7100–40,400) in Wuhan, while the number would be less than one-third of the number in the actual scenario and the peaks would arrive ten days earlier (Fig. 6c). The early action scenario would have a larger reduction in the size of the affected population across the entire country, and the cumulative infected population would be 65,200 (95% CI 42,000–120,900) and the total number of deaths would have been 1500 (95% CI 970–2780) or only a quarter of the predicted actual scenario. This shows the importance of early intervention. According to our simulation, the infected population and the number of deaths would decay exponentially with the advance of intervention time, at a rate of 0.212 (95% CI 0.208–0.219) in a log2 base, indicating that if the intervention time was advanced by 5 days, the total number of infected people would be reduced to half of the present total. This conclusion is similar as in [32].

3.6 Less effective scenario (\(t_{0} = 22, \;\lambda = 0.2, \;t^{*} \to \infty\)).

We also consider a less effective scenario in which the intervention strength is weaker than the actual situation which means the reproduction number would be reduced to \(\epsilon R_{0} = 0.002\) in about 70 days (\(\lambda = 0.2\)), the infected individuals in Wuhan would peak at 0.27 million (95% CI 0.12–1.15) in early March (Fig. 6e). The total number of deaths in mainland China would increase to 63,000 (95% CI 38,700–149,800).

3.7 Early action but less effective scenario (\(t_{0} = 12, \;\lambda = 0.2,\; t^{*} \to \infty\)).

This scenario corresponds to the policy that most of European countries have implemented, that is implementing the intervention earlier (\(t_{0} = 12\)) but with less strict enforcement (\(\lambda = 0.2\)). The predicted number of cumulative infectious cases and death cases would be 652,000 (95% CI 403,000–1,490,000) and 15,000 (9270–34,200).

We summarize the predicted cumulative infected and confirmed cases after the epidemic in different scenarios in Fig. 6.

3.8 Intervention relaxation (\(t_{0} = 22, \;\lambda = 0.4, \;0 < t^{*} < \infty\))

Under the actual scenario (\(\lambda = 0.4, \;t_{0} = 22\)), the earliest date \(t^{*}\) across all cities to relax the intervention to avoid resurgence is around the 81st day (i.e., March 22, 2020), that means the tough intervention should be maintained for about eight weeks. In the early action but less effective scenario, the measure would have to be maintained for about 12 weeks, see SI Section 3 for details.

4 Discussion

In this study, we proposed a five-state model and estimated the spreading dynamics of COVID-19 within China by analyzing the latest national population mobility data. The model can capture the early exponential growth of the outbreak at the city level, as well as perform scenario analyses based on different strengths of prevention interventions and time of start and relaxation.

Both the time of starting an intervention and its strength play important roles in controlling the outbreak size. Without any population intervention, the virus would have spread extensively through the population with over one billion cases (~ 85% of population) in China and with nearly 27 million deaths. The current Chinese city policy has reduced the impact substantially but would have been even more effective had it started earlier.

Our model shows that the intervention needs to be sustained for about eight weeks to prevent a recurrent epidemic. Moreover, if it had been less effective in preventing population mixing, which may be the case in many other countries, then the number of cases and deaths would increase significantly, and by tenfold under the assumptions of our less effective scenario.

Our estimation of the basic reproduction number \(R_{0}\) is slightly lower than some previous literature: 2.47–2.86 [23], 2.28–3.68 [22], and 2.39–4.13 [26], as we estimated this using the actual data to February 7, which includes two weeks after effective measures to reduce population mixing began in China. Comparing our findings with others then for the number of infected cases, our prediction for Wuhan is smaller than some recent works: 37,304–130,330 as of January 25 [24] and 11,090–33,490 as of January 22 [31] because they may have overestimated \(R_{0}\) or did not take the strong intervention into account. In other major cities, our result is broadly consistent with others [24].

Our work demonstrates the value of data sharing and information disclosure [43]. All the data used in this article came from public sources, including data released by large companies (migration data), as well as by start-ups such as DXY.cn, a Chinese physician’s platform [44]. We notice that many volunteers are also working on collecting data via crowdsourcing, and several applications have been developed immediately [45].

However, despite adopting a state-of-the-art modeling framework, we must acknowledge that our model has several major limitations. First, we assume that different cities share the same model parameters. However, the geographical location, demographic structure, and level of city governance of different cities are different, and thus, the actual disease transmission parameters are likely to be different. Second, the case data and mobile phone data used in training the model are as of February 7, 2020, and the fatality data are also based on the results of early patient studies [40]. If updated and more recent data were added, the model's predictive performance could be improved (SI Section 3). Third, our model did not consider imported or exported cases between China and other countries. Given global mobility network data and reported case data, further analysis can be extended to simulate infection in different countries, which could be of crucial importance for public health planning, transportation intervention, and logistics support at the current stage, when large-scale outbreaks of COVID-19 are happening in Europe, Iran, and other regions.

The intense social distancing intervention in China has been effective in limiting the scale of the epidemic but needs to be sustained. The model suggests that delay in start and a less effective intervention would increase the number of cases and deaths substantially and prolong the period of social distancing and other control measures.