Furin and the adaptive mutation of SARS-COV2: a computational framework

Abstract

SARS-2 virus has reached its most harmful mutated form and has damaged the world’s economy, integrity, health system and peace to a limit. An open problem is to address the release of antibodies after the infection and after getting the individuals vaccinated against the virus. The viral fusion process is linked with the furin enzyme and the adaptation is linked with the mutation, called D614G mutation. The cell-protein studies are extremely challenging. We have developed a mathematical model to address the process at the cell-protein level and the delay is linked with this biological process. Genetic algorithm is used to approximate the parametric values. The mathematical model proposed during this research consists of virus concentration, the infected cells count at different stages and the effect of interferon. To improve the understanding of this model of SARS-CoV2 infection process, the action of interferon (IFN) is quantified using a variable for the non-linear mathematical model, that is based on a degradation parameter $\gamma$. This parameter is responsible for the delay in the dynamics of this viral action. We emphasize that this delay responds to the evasion by SARS-CoV2 via antagonizing IFN production, inhibiting IFN signaling and improving viral IFN resistance. We have provided videos to explain the modeling scheme.

Introduction

The impact of the CoViD-19 disease is devastating and scientific research seek to understand the mechanisms of infection to create vaccine with least side-effects and most promising results against the mutated virus. Scientists have reported that Arg-Arg-Ala-Arg (RRAR) is a cleavage site for furin enzyme. The furin action on S protein permit a faster activation and greatest rate of infection.. The furin site Is on SARS-COV2 but not in SARS-CoV or MERS-CoV. It is responsible for the high infection rates and transmission rates of SARS-CoV2. The presence of the this cleavage site is experimentally proven Walls et al. (2020) and the Activation of S requires proteolytic cleavage at two distinct sites: in the unique multibasic site motif RRAR, located between the S1 and S2 subunits, and within the S2 subunit (“S2”) located immediately upstream of the hydrophobic fusion peptide that is responsible for triggering virus-cell membrane fusion. This event, although not exclusive to SARS-CoV2, is important because it is absent on the viral antigens of the same viral family Coutard et al. (2020); Yu et al. (2021). It is important to consider this characteristic because it implies a greater speed of action of SARS-CoV2 than, for example, SARS-CoV, so much so that some adaptive mutations such as D614G seem to carry out structural changes that more expose the cut site for furin Korber et al. (2020).

In this article, we are focusing on the speed of action of SARS-2 inspired by the experimental study of Papa et’al. Papa et al. (2021). The exclusive action of the cutting site of furin, that is present in SARS-2 is still an open problem.

The work of Buonvino and Melino (2020) identifies viral evolution from the RaTG13 genotype and shows how, for SARS-CoV2, the acquisition of the furin cleavage site implies greater instability of the S protein. This is a very important factor for understanding the dynamics of the infection. For the infectious process to begin, some key enzymes play important role. For example, Furin” contributes to split the S protein into two subunits: S1 and S2. Therefore, it facilitate the fusion between the viral membrane and that of the host cell. SARS-CoV2 presents a further modified cleavage site for furin, i.e. in the amino acids of this site, a proline is added that changes the sequence and allows a strong bending of the structure leading to the introduction of three glycans O-linked that line the site itself. Furthermore, the furin-promotes infection capacity as well as the adaptive mutation. SARS-CoV2 virus has acquired a cleavage site for furin between S1 and S2 that appears to promote pathogenicity. This fact, in addition to enhancing the viral pathogenic aspect, also seems to be responsible for the speed of infection, especially in connection with the presence of an adaptive mutation “D614G”. “D614G mutation” neither increases S protein affinity for ACE2 nor makes viral particle more resistant to neutralization and that TMPRSS2 and Furin of all species studied can cleave the SARS-CoV-2 S glycoprotein in a similar way, provided that they are well conserved proteases among many species Brooke and Prischi (2020). For further details, please see video S1 and S2.

By taking into account these properties of Furin, we have hypothesized that the high rate of infection occurs when there is the presence of this adaptive mutation together with a structural adaptation of the clevage site of the furin on the viral protein S.

It is highly desired to explore the complex mechanism of action of this highly infectious virus. The improved understanding of the structural features of SARS-COV2 (as provided in the supplementary videos) can help to design targeted therapies. Applied mathematical models can help to explore the dynamics of these interactions more accurately Al-Utaibi et al. (2021); Yu et al. (2020); Abdel-Salam et al. (2021); Yu et al. (2021). In this manuscript, we have worked on a model that is linked with SARS-COV2 infection mechanism. The mathematical approach demonstrates how SARS-COV2 is more efficient and adapted to human cells. The model is developed with the aid of the cell-protein interaction studies, available in the literature. The concept of delay has not only proved to be an important, but a deadly weapon of this virus. Our mathematical model features this line of action of SARS-COV2 more accurately.

The rest of the manuscript is organized as follows: In Sect. 2, the mathematical model with delay is presented.

In Sect. 3, the stability analysis, HOPF bifurcation, hybrid genetic algorithm and important cases are presented.

In Sect. 4, important results are discussed and at the end, useful conclusions are drawn.

Model development

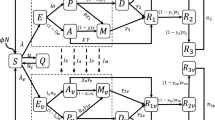
To develop the model, we need to first synchronize the biological phenomena with the mathematical modeling procedure. For this the details are provided in videos S1 and S2. The schematic can also be understood with the aid of Fig. 1.

Scheme of the viral adaptation of SARS-CoV2 in the improvement of the infectious process. (A) Acquisition of the adaptive mutation D614G; (B) Structural adaptive modification for the furin cleavage site; (C) Protein S structured from the complex of adaptive modifications that improves the rate of viral infection.

Fig. 1

Schematic depiction of the model

Computational tools have always helped to explore the biological phenomena in a cost effective manner Nutini and Sohail (2020). These methods includes modeling, simulation and forecasting tools. The viral pathology can be interpreted with the aid of mathematical models Belz et al. (2002); Iftikhar et al. (2020). The treatment strategies can be explored with the aid of the mathematical models in an efficient manner, at different scales. Dynamics at cellular, subcelluar and molecular scales can be modeled with the aid of the hybrid modeling approaches Iftikhar et al. (2020).

In this manuscript, we have developed a model, inspired by the work of Pawelek et al. (2012); Sohail and Nutini (2020); Brooke and Prischi (2020); Bhowmik et al. (2020, 2020); Hoffmann et al. (2020); Caufield et al. (2018); Chen et al. (2020); Kleine-Weber et al. (2018) and the references therein. The model is based on the virus concentration, the target cells, the infected cells at levels 1 & 2 (two levels of action are discussed in the introduction (see Fig. 1 as virus infected cells and virus spreading cells) and the IFN signaling proteins.

$$\begin{aligned} \frac{{{\text{d}}V}}{{{\text{d}}t}} & = \frac{{bZ}}{{c_{2} F + 1}} - \kappa V,\frac{{{\text{d}}X}}{{{\text{d}}t}} = \rho - \eta VX - {\text{d}}X, \\ \frac{{{\text{d}}Y}}{{{\text{d}}t}} & = \eta X\left( {t - \tau _{1} } \right)V(t - \tau _{1} ) - \frac{{aY}}{{c_{1} F + 1}}, \\ \frac{{{\text{d}}Z}}{{{\text{d}}t}} & = \frac{{aY}}{{c_{1} F + 1}} - rZ\left( {t - \tau _{2} } \right)F\left( {t - \tau _{2} } \right) - \psi Z, \\ \frac{{{\text{d}}F}}{{{\text{d}}t}} & = rZ\left( {t - \tau _{2} } \right) - \gamma F. \\ \end{aligned}$$

(1)

With initial conditions

$$\begin{aligned} V(\phi )&=\omega _1(\phi )\ge 0,\\ X(\phi )&=\omega _2(\phi )\ge 0,\\ Y(\phi )&=\omega _3(\phi )\ge 0,\\ Z(\phi )&=\omega _4(\phi )\ge 0,\\ F(\phi )&=\omega _5(\phi )\ge 0,\\&\phi \in [-\tau ,0],\\&\tau =\min \{\tau _1,\tau _2\}. \end{aligned}$$

(2)

Description of variables and parameters is in Tables (1) and (2) and the dynamics can be well understood with the aid of Fig. 2.

Table 1 Description of Compartments

Table 2 Description of parameter

Fig. 2

Schematic depiction of the model

Positivity of solutions specifies the existence of cells.

Theorem 2.1

Assume that initial solution $V(0)\ge 0$, $X(0)\ge 0$, $Y(0)\ge 0$, $Z(0)\ge 0$ and $F(0)\ge 0$, then the solution of model (1) are non-negative $\forall$ $t>0$.

Proof: From 2nd equation of model all the parameters has positive values, as $\rho >0$

$${\frac{{{\text {d}}X}} {{{\rm{d}}t}}} \ge - \eta VX - {\text{d}}X$$

(3)

By integrating we obtain

$$\begin{aligned} X(t)\ge X(0) \exp \left\{ -d - \eta V(t)\right. t \end{aligned}$$

(4)

the above expression shows that X(t) depends on X(0). Therefore, X(t) is positive if X(0) is non negative.

First equation of model (1)

$$\frac{{{\text{d}}V}}{{{\text{d}}t}} = \frac{{bZ}}{{c_{2} F + 1}} - \kappa V,{\text{ }}V(t) \ge V(0)\exp \{ - \kappa t\} .{\text{ }}$$

(5)

Similarly for third, four and fifth equation of the model we have following results

$$\begin{aligned} Y(t)&\ge Y(0)\exp \{-\frac{a t}{c_1 F+1}\},\\ Z(t)&\ge Z(0)\exp \{-\psi \} +\int _0^t \exp \{-\psi \}\frac{a Y(t)}{c_1 F(t)+1}dt,\\ F(t)&\ge F(0) \exp \{-\gamma \}. \end{aligned}$$

(6)

From equation 4, 5, and 6 it is easily seen that if initial solution is non negative then the solution for all values of time t is non negative.

Equilibrium points

The model (1) has infection free equilibrium point, gain by putting right hand side of equation of the model (1) equal to zero

$$\begin{aligned} E_0=(V_0, X_0, Y_0, Z_0, F_0)=(0, \frac{\rho }{d}, 0, 0, 0). \end{aligned}$$

(7)

The linear stability of model is established with method of next-generation operator on model. The reproduction number of model, indicated by $R_0$, can calculated as

$$\begin{aligned} R_0=\frac{b \eta \rho }{d \kappa \psi }. \end{aligned}$$

(8)

The capability of virus to produce infection or to be uninfected can be analyzed by basic reproductive number $R_0=\frac{b \eta \rho }{d \kappa \psi }$. With $R _0 <1$ refers to a decrease in virus production of infected cells where as $R_0 >1$ infection produce due to the increase in virus infected cells production.

Existence of equilibrium points

Theorem 2.2

The model has exclusive endemic equilibrium point if and only if $R_0>1$.

Proof: By calculating endemic equilibrium point, we get

$$\begin{aligned} E^*=(V^*, X^*, Y^*, Z^*, F^*) \end{aligned}$$

(9)

where:

$$\begin{aligned} V^*&=\frac{\gamma \left( A-b \eta \left( 2 c_2 \rho r+\gamma \psi \right) -d \kappa r \left( r-c_2 \psi \right) \right) }{2 \eta \kappa r \left( \gamma r-c_2 \left( c_2 \rho r+\gamma \psi \right) \right) },\\ X^*&=\frac{\kappa \left( A \gamma +b \gamma \eta \left( 2 c_2 \rho r+\gamma \psi \right) +d \kappa r \left( \gamma c_2 \psi +2 c_2^2 \rho r-\gamma r\right) \right) }{2 \left( b \gamma \eta +c_2 d \kappa r\right) {}^2},\\ Y^*&=\frac{\gamma \left( b^3 \gamma ^2 \eta ^3 \rho \left( 2 r-c_1 \psi \right) -\left( c_2-c_1\right) d^2 \kappa ^2 r^2 \left( A+d \kappa r \left( c_2 \psi -r\right) \right) \right) }{2 a r \left( b \gamma \eta +c_2 d \kappa r\right) {}^3}\\&\quad +\frac{\gamma \left( b d \eta \kappa r \left( d \kappa r \left( \psi \left( -2 \gamma c_2+\gamma c_1-c_1 c_2^2 \rho \right) +r \left( \left( 2 c_2-3 c_1\right) c_2 \rho +\gamma \right) \right) \right) \right) }{2 a r \left( b \gamma \eta +c_2 d \kappa r\right) {}^3}\\&\quad +\frac{\gamma \left( \left( +b^2\right) \gamma \eta ^2 \left( A c_1 \rho +d \kappa r \left( \left( 4 c_2-3 c_1\right) \rho r-\psi \left( 2 c_1 c_2 \rho +\gamma \right) \right) \right) +A b d \eta \kappa r \left( c_1 c_2 \rho -\gamma \right) \right) }{2 a r \left( b \gamma \eta +c_2 d \kappa r\right) {}^3},\\ Z^*&=\frac{\gamma }{r}(\frac{A-b \gamma \eta \psi -d \kappa r \left( c_2 \psi +r\right) }{2 r \left( b \gamma \eta +c_2 d \kappa r\right) }),\\ F^*&=\frac{A-b \gamma \eta \psi -d \kappa r \left( c_2 \psi +r\right) }{2 r \left( b \gamma \eta +c_2 d \kappa r\right) },\\ A&=\sqrt{4 r^2 (b \eta \rho -d \kappa \psi ) \left( b \gamma \eta +c_2 d \kappa r\right) +\left( b \gamma \eta \psi +c_2 d \kappa r \psi +d \kappa r^2\right) {}^2}. \end{aligned}$$

(10)

Results

Stability analysis and the Hopf bifurcation

Here we examine qualitative behavior of the model (1) by analyzing local stability of equilibrium points and Hopf bifurcation, which presents the behavior of model (1) by a small change of the solutions as reaction to changes in the particular parameter. As time delays have the significant effect in complexity and dynamics of this model (1), we will assume them as the parameter of bifurcation. Now we examine stability at endemic equilibrium point, the Jacobian matrix at $E^*$ is

$$\begin{aligned} J^*=\left( \begin{array}{lllll} -\kappa &{} 0 &{} 0 &{} b &{} 0 \\ G_1 &{} -d &{} 0 &{} 0 &{} 0 \\ G_2 e^{-\lambda \tau _1}+G_1 &{} e^{-\lambda \tau _1} G_3 &{} -a &{} 0 &{} 0 \\ 0 &{} 0 &{} a &{} e^{-\lambda \tau _2} G_4-\psi &{} 0 \\ 0 &{} 0 &{} 0 &{} r e^{-\lambda \tau _2}+r &{}-\gamma \\ \end{array} \right) \end{aligned}$$

(11)

where

$$\begin{aligned} G_1&=-\frac{\eta \lambda }{d},\\ G_2&=\eta X^*,\\ G_3&=\eta V^*,\\ G_4&=-F^* r-\psi . \end{aligned}$$

(12)

The characteristic equation at endemic equilibrium point is

$$\begin{aligned} \upsilon _1(\lambda )+e^{-\lambda \tau _1}\upsilon _2(\lambda )+e^{-\lambda \tau _2}\upsilon _3(\lambda )=0 \end{aligned}$$

(13)

where

$$\begin{aligned} \upsilon _1(\lambda )&=\lambda ^5+\alpha _1 \lambda ^4+\alpha _2 \lambda ^3+\alpha _3 \lambda ^2+\alpha _4 \lambda +\alpha _5,\\ \upsilon _2(\lambda )&=\beta _1 \lambda ^4+\beta _2 \lambda ^3+\beta _3 \lambda ^2+\beta _4 \lambda +\beta _5,\\ \upsilon _3(\lambda )&=\gamma _1 \lambda ^4+\gamma _2 \lambda ^3+\gamma _3 \lambda ^2+\gamma _4 \lambda +\gamma _5. \end{aligned}$$

(14)

The coefficients are

$$\begin{aligned} \alpha _1&=a+\gamma +d+\kappa +\psi ,\\ \alpha _2&=a (\gamma +d+\kappa +\psi )+\psi (\gamma +\kappa )+\gamma \kappa +d (\gamma +\kappa +\psi ),\\ \alpha _3&=-a b G_1+a (\gamma (\kappa +\psi )+d (\gamma +\kappa +\psi )+\kappa \psi )+\gamma \kappa \psi +d \psi (\gamma +\kappa )+\gamma d \kappa ,\\ \alpha _4&=-a b G_1 (\gamma +d)+\psi (a \kappa (\gamma +d)+a \gamma d+\gamma d \kappa )+a \gamma d \kappa ,\\ \alpha _5&=a \gamma d \left( \kappa \psi -b G_1\right) ,\\ \beta _1&=0,\\ \beta _2&=0,\\ \beta _3&=-a b G_2,\\ \beta _4&=-ab\left( G_2 (\gamma +d)+G_1 G_3\right. ),\\ \beta _5&=aa b \gamma \left( -d G_2-G_1 G_3\right) ,\\ \gamma _1&=-G_4,\\ \gamma _2&=-G_4 (a+\gamma +d+\kappa ),\\ \gamma _3&=-G_4 (a (\gamma +d+\kappa )+\gamma \kappa +d (\gamma +\kappa )),\\ \gamma _4&=-G_4 (a \kappa (\gamma +d)+a \gamma d+\gamma d \kappa ),\\ \gamma _5&=a \gamma d G_4 \kappa . \end{aligned}$$

(15)

Here, we discuss stability of endemic equilibrium and Hopf bifurcation conditions of the threshold parameters such as $\tau _1$ and $\tau _2$ by assuming different cases.

Case 1. When both delay $\tau _1$,and $\tau _2$ are zero equation (13) become

$$\begin{aligned}&\lambda ^5+\lambda ^4 \vartheta _1+\lambda ^3 \vartheta _2+\lambda ^2 \vartheta _3+\lambda \vartheta _4+\vartheta _5=0. \end{aligned}$$

(16)

Endemic equilibrium is asymptotically stable by Routh-Hurwitz Criteria if

$$\begin{aligned}&(R_1) (\alpha _i+\beta _i+\gamma _i)>0, \vartheta _1\vartheta _2\vartheta _3>\vartheta _2^2+\vartheta _1^2\vartheta _4,\\&and\\&(\vartheta _1\vartheta _4-\vartheta _5)(\vartheta _1\vartheta _2\vartheta _3\vartheta _3^2-\vartheta _1^2\vartheta _4)>\vartheta _1\vartheta _5^2+\vartheta _5(\vartheta _12-\vartheta _3^2) \end{aligned}$$

(17)

holds, then all the roots are negative. Where $\vartheta _i=\left( \alpha _i+\beta _i+\gamma _i\right)$ and $i=1:5$.

Case 2. For $\tau _1=0$ and $\tau _2$ is a real positive number, equation (13) turn out to be

$$\begin{aligned}&\lambda ^5+\lambda ^4 \left( \alpha _1+\beta _1\right) +\lambda ^3 \left( \alpha _2+\beta _2\right) +\lambda ^2 \left( \alpha _3+\beta _3\right) +\lambda \left( \alpha _4+\beta _4\right) +\alpha _5+\beta _5+\\&e^{-\lambda \tau _2}\left( \gamma _1 \lambda ^4+\gamma _2 \lambda ^3+\gamma _3 \lambda ^2+\gamma _4 \lambda +\gamma _5\right) =0. \end{aligned}$$

(18)

We suppose that there exists real positive number $\psi$ for some value of $\tau _1$ in such a way that $\lambda = i\psi$ is the root of (18), then we have two equations

$$\begin{aligned} \psi ^4 \left( \alpha _1+\beta _1\right) -\psi ^2 \left( \alpha _3+\beta _3\right) +\alpha _5+\beta _5&=- \gamma _1 \psi ^4\cos \tau _2 \psi + \gamma _3 \psi ^2\cos \tau _2 \psi \\&\quad - \gamma _5\cos \tau _2 \psi -\gamma _2 \psi ^3\sin \tau _2 \psi -\gamma _4 \psi \sin \tau _2 \psi ,\\ -\psi ^3 \left( \alpha _2+\beta _2\right) +\psi \left( \alpha _4+\beta _4\right) +\psi ^5&= \gamma _2 \psi ^3\cos \tau _2 \psi - \gamma _4 \psi \cos \tau _2 \psi +\gamma _1 \psi ^4\sin \tau _2 \psi \\&\quad -\gamma _3 \psi ^2\sin \tau _2 \psi +\gamma _5 \sin \tau _2 \psi . \end{aligned}$$

(19)

After simplifying these equation we have

$$\begin{aligned} \psi ^{10}+\psi ^8 \varkappa _1+\psi ^6 \varkappa _2+\psi ^4 \varkappa _3+\psi ^2 \varkappa _4+\varkappa _5=0 \end{aligned}$$

(20)

where the constants are

$$\begin{aligned} \varkappa _1&=\left( \alpha _1+\beta _1\right) {}^2-2 \left( \alpha _2+\beta _2\right) -\gamma _1^2,\\ \varkappa _2&=\left( \alpha _2+\beta _2\right) {}^2-2 \left( \alpha _1+\beta _1\right) \left( \alpha _3+\beta _3\right) +2 \alpha _4+2 \beta _4-\gamma _2^2+2 \gamma _1 \gamma _3,\\ \varkappa _3&=\left( \alpha _3+\beta _3\right) {}^2-2 \left( \alpha _2+\beta _2\right) \left( \alpha _4+\beta _4\right) +2 \left( \alpha _1+\beta _1\right) \left( \alpha _5+\beta _5\right) -\gamma _3^2-2 \left( \gamma _2 \gamma _4+\gamma _1 \gamma _5\right) ,\\ \varkappa _4&=\left( \alpha _4+\beta _4\right) {}^2-2 \left( \alpha _3+\beta _3\right) \left( \alpha _5+\beta _5\right) -\gamma _4^2+2 \gamma _3 \gamma _5,\\ \varkappa _5&=\left( \alpha _5+\beta _5\right) {}^2-\gamma _5^2. \end{aligned}$$

(21)

By rule of signs of Descartes, equation (19) has as a minimum one positive root if $(S_1)\left( \alpha _1+\beta _1\right) {}^2>2 \left( \alpha _2+\beta _2\right) +\gamma _1^2$ and $\left( \alpha _5+\beta _5\right) {}^2<\gamma _5^2$ holds.

By eliminating $\sin \tau _1 \psi$ form equation (19) we have

$$\begin{aligned} \tau _{2,j}=\dfrac{1}{\psi _0}\arccos [\frac{\rho _1 \rho _3+\rho _2 \rho _4}{\rho _1^2-\rho _2^2}]+\dfrac{2 \pi j}{\psi _0},j=0,1,2,\ldots \end{aligned}$$

(22)

where

$$\begin{aligned} \rho _1&=\gamma _2 \psi ^3+\gamma _4 \psi ,\\ \rho _2&=\gamma _1 \psi ^4-\gamma _3 \psi ^2+\gamma _5,\\ \rho _3&=-\psi ^3 \left( \alpha _2+\beta _2\right) +\psi \left( \alpha _4+\beta _4\right) +\psi ^5,\\ \rho _4&=\psi ^4 \left( \alpha _1+\beta _1\right) -\psi ^2 \left( \alpha _3+\beta _3\right) +\alpha _5+\beta _5. \end{aligned}$$

(23)

Differentiating equation (18) with respect to delay $(\tau _2)$ with the assumption of $\psi =\psi _0$, then transversality form is obtain

$$\begin{aligned} Re(\dfrac{d \lambda }{d \tau _2})^{-1}=\frac{T_1 T_4-T_3 T_2}{T_4 T_2}, \end{aligned}$$

(24)

where

$$\begin{aligned} T_1&=\left( -3 \psi ^2 \left( \alpha _2+\beta _2\right) +\alpha _4+\beta _4+5 \psi ^4\right) \\&\qquad \left( \psi ^4 \left( \alpha _2+\beta _2\right) -\psi ^2 \left( \alpha _4+\beta _4\right) +\beta _5-\psi ^6\right) ,\\ T_2&=\left( \psi ^5 \left( \alpha _1+\beta _1\right) -\psi ^3 \left( \alpha _3+\beta _3\right) +\alpha _5 \psi \right) {}^2\\&\quad +\left( -\psi ^4 \left( \alpha _2+\beta _2\right) +\psi ^2 \left( \alpha _4+\beta _4\right) -\beta _5+\psi ^6\right) {}^2,\\ T_3&=\left( \gamma _4-3 \gamma _2 \psi ^2\right) \left( \gamma _2 \psi ^4-\gamma _4 \psi ^2\right) ,\\ T_4&= \left( \gamma _2 \psi ^4-\gamma _4 \psi ^2\right) {}^2-\left( \gamma _1 \psi ^5-\gamma _3 \psi ^3+\gamma _5 \psi \right) {}^2. \end{aligned}$$

(25)

The hopf bifurcation arise for delay $(\tau _2)$ if $Re(\dfrac{d \lambda }{d \tau _2})^{-1}>0$. The above analysis is summarized in following theorem.

Theorem 3.1

Assume that $R_1$ and $S_1$ holds, where delay $\tau _1=0$, in that case, there exist $\tau _2>0$ such that $E^*$ is locally asymptotically stable for $\tau _2<\tau _2^*$ and unstable for $\tau _2>\tau _2^*$, where $\tau _2^*=\min \{\tau _{2,j}\}$ in equation (22). Furthermore, at $\tau _2=\tau _2^*$ the model (1) undergoes Hopf bifurcation at endemic equilibrium point.

Case 3. When $\tau _1> 0$ and $\tau _2= 0$, in same procedure of case (2), we reach at subsequent theorem.

Theorem 3.2

For model (1) where $\tau _2=0$, in that case, there exist $\tau _1>0$ such that $E^*$ is locally asymptotically stable for $\tau _1<\tau _1^*$ and unstable for $\tau _1>\tau _1^*$, where $\tau _1^*=\min \{\tau _{1,j}\}$ in equation (26). Furthermore, at $\tau _1=\tau _1^*$ the model (1) undergoes Hopf bifurcation at endemic equilibrium point,

$$\begin{aligned} \tau _{1,j}=\dfrac{1}{\psi _1}\arccos \{\frac{\delta _1 \delta _2+\delta _3 \delta _4}{\delta _1^2-\delta _3^2}\}+\dfrac{2 \pi j}{\psi _1},j=0,1,2,\ldots \end{aligned}$$

(26)

where

$$\begin{aligned} \delta _1&=\psi _1 \left( \beta _4 \psi _1 -\beta _2 \psi ^3_1\right) ,\\ \delta _2&=-\psi ^2_1 \left( \alpha _2+\gamma _2\right) +\alpha _4+\gamma _4+\psi ^4_1,\\ \delta _3&=-\beta _1 \psi ^4_1+\beta _3 \psi ^2_1-\beta _5,\\ \delta _4&=\psi ^4_1 \left( \alpha _1+\gamma _1\right) -\psi ^2_1 \left( \alpha _3+\gamma _3\right) +\alpha _5+\gamma _5. \end{aligned}$$

(27)

Case 4. When both $\tau _1$ and $\tau _2$ are positive. Then, suppose that $\tau _2$ as variable and $\tau _1$ is fixed parameter on stable interval. Assume that there exist a number $\psi$ such that $\lambda =i \psi$ is the root of (13), we obtain

$$\begin{aligned}&\alpha _1 \psi ^4-\alpha _3 \psi ^2+\alpha _5+\left( \beta _1 \psi ^4-\beta _3 \psi ^2+\beta _5\right) \cos \tau _1 \psi + \left( \beta _2 \psi ^3+\beta _4 \psi \right) \sin \tau _1 \psi \\&=\left( \gamma _2 \psi ^3-\gamma _4 \psi \right) \sin \tau _2 \psi - \left( \gamma _1 \psi ^4-\gamma _3 \psi ^2+\gamma _5\right) \cos \tau _2 \psi ,\\&-\alpha _2 \psi ^3+\alpha _4 \psi + \left( \beta _4 \psi -\beta _2 \psi ^3\right) \cos \tau _2 \psi +\left( -\beta _1 \psi ^4+\beta _3 \psi ^2-\beta _5\right) \sin \tau _2 \psi +\psi ^5\\&= \left( \gamma _2 \psi ^3-\gamma _4 \psi \right) \cos \tau _1 \psi +\left( \gamma _1 \psi ^4-\gamma _3 \psi ^2+\gamma _5\right) \sin \tau _1 \psi . \end{aligned}$$

(28)

After simplifying we have

$$\begin{aligned} \varsigma _5+\psi ^{10}+\psi ^8 \varsigma _1+\psi ^6 \varsigma _2+\psi ^4 \varsigma _3+\psi ^2 \varsigma _4=0. \end{aligned}$$

(29)

Where:

$$\begin{aligned} \varsigma _1&=\alpha _1^2-2 \alpha _2+\beta _1^2+2\left( \alpha _1 \beta _1-\beta _2\right) \cos \tau _1 \psi -\gamma _1^2,\\ \varsigma _2&=\alpha _2^2+\beta _2^2+2 \left( -\alpha _1 \alpha _3+\alpha _4-\beta _1 \beta _3+\alpha _2 \beta _2 \cos \tau _1\psi \right) \\&\quad -2 \left( \alpha _3 \beta _1+\alpha _1 \beta _3-\beta _4\right) \cos \tau _1\psi +2\gamma _1 \gamma _3-\gamma _2^2,\\ \varsigma _3&=2 \left( -\alpha _2 \alpha _4+\beta _1 \beta _5+\gamma _2 \gamma _4-\gamma _1 \gamma _5\right) +\alpha _3^2-\beta _2 \beta _4 \left( \cos \tau _1\psi ^2-\sin \tau _1\psi ^2\right) \\&\quad +2 \left( \alpha _1 \alpha _5+ \left( \alpha _5 \beta _1-\alpha _4 \beta _2+\alpha _3 \beta _3-\alpha _2 \beta _4+\alpha _1 \beta _5\right) \cos \tau _1\psi \right) +\beta _3^2-\gamma _3^2,\\ \varsigma _4&=\alpha _4^2+\beta _4^2+2 \left( -\alpha _3 \alpha _5-\beta _3 \beta _5+\left( -\alpha _5 \beta _3+\alpha _4 \beta _4-\alpha _3 \beta _5\right) \cos \tau _1\psi +\gamma _3 \gamma _5\right) -\gamma _4^2,\\ \varsigma _5&=-\alpha _4 \beta _1+\alpha _5^2+\beta _5^2+2 \alpha _5 \beta _5 \cos \tau _1\psi -\gamma _5^2. \end{aligned}$$

(30)

By applying rule of signs of Descartes equation (29) has minimum one positive root if $(S_2)$ $\alpha _1^2-2 \alpha _2+\beta _1^2+2\left( \alpha _1 \beta _1-\beta _2\right) \cos \tau _1 \psi -\gamma _1^2>0$ and $\varsigma _5<0$ holds. we have

$$\begin{aligned} \tau _{2,j}=\dfrac{1}{\psi _2}\arccos \{\frac{\rho _1 \rho _5-\rho _6 \rho _2}{\rho _1^2+\rho _2^2}\}+\dfrac{2 \pi j}{\psi _2}, j=0,1,2,\ldots \end{aligned}$$

(31)

with

$$\begin{aligned} \rho _5&=\alpha _2 \psi _2 ^3-\alpha _4 \psi _2 -\delta _1\cos \tau _1\psi _2-\delta _3 \sin \tau _1\psi _2-\psi _2 ^5,\\ \rho _6&=\alpha _1 \psi _2 ^4-\alpha _3 \psi _2 ^2+\alpha _5+ \delta _3\cos \tau _1\psi _2+\delta _1 \sin \tau _1\psi _2. \end{aligned}$$

(32)

For Hopf bifurcation $\tau _1$ will be fixed and differentiate with respect to $\tau _2$ in equation (28) by putting $\tau _2=\tau _{2,0}$ at $\psi =\psi _3$,

$$\begin{aligned} V_1(\dfrac{d\lambda }{d\tau _2}|\tau _2=\tau _{2,0})+V_2(\dfrac{d\psi }{d\tau _2}|\tau _2=\tau _{2,0})&=V_3,\\ V_2(\dfrac{d\lambda }{d\tau _2}|\tau _2=\tau _{2,0})-V_1(\dfrac{d\psi }{d\tau _2}|\tau _2=\tau _{2,0})&=V_4. \end{aligned}$$

(33)

where

$$\begin{aligned} V_1&=\left( \tau _{2,0} \left( \gamma _2 \psi _3 ^3-\gamma _4 \psi _3 \right) -4 \gamma _1 \psi _3 ^3+\psi _3 \left( \gamma _2 \psi _3 ^3-\gamma _4 \psi _3 \right) +2 \gamma _3 \psi _3 \right) \cos \tau _{2,0}\psi _3\\&\quad +\left( \tau _{2,0} \left( \gamma _1 \psi _3 ^4-\gamma _3 \psi _3 ^2+\gamma _5\right) +3 \gamma _2 \psi _3 ^2-\psi _3 \left( \gamma _1 \psi _3 ^4-\gamma _3 \psi _3 ^2+\gamma _5\right) -\gamma _4\right) \sin \tau _{2,0}\psi _3,\\ V_2&= \left( \tau _{2,0} \left( \gamma _1 \psi _3 ^4-\gamma _3 \psi _3 ^2+\gamma _5\right) +3 \gamma _2 \psi _3 ^2+\psi _3 \left( \gamma _1 \psi _3 ^4-\gamma _3 \psi _3 ^2+\gamma _5\right) -\gamma _4\right) \cos \tau _{2,0}\psi _3\\&\quad + \left( \tau _{2,0} \left( \gamma _2 \psi _3 ^3-\gamma _4 \psi _3 \right) -\psi _3 \left( \gamma _2 \psi _3 ^3-\gamma _4 \psi _3 \right) +4 \gamma _1 \psi _3 -2 \gamma _3 \psi _3 \right) \sin \tau _2\psi _3,\\ V_3&=3 \alpha _1 \psi _3 ^3-2 \alpha _3 \psi _3 + \left( \tau _1 \left( \beta _2 \psi _3 ^3+\beta _4 \psi _3 \right) +4 \beta _1 \psi _3 ^3-2 \beta _3 \psi _3 \right) \cos \tau _1\psi _3\\&\quad +\left( \left( 3 \beta _2 \psi _3 ^2+\beta _4\right) -\tau _1 \left( \beta _1 \psi _3 ^4-\beta _3 \psi _3 ^2+\beta _5\right) \right) \sin \tau _1\psi _3,\\ V_4&=-3 \alpha _2 \psi _3 ^2+\alpha _4+\left( \tau _1 \left( -\beta _1 \psi _3 ^4+\beta _3 \psi _3 ^2-\beta _5\right) \cos \tau _1\psi _3-3 \beta _2 \psi _3 ^2+\beta _4\right) \\&\quad +\left( -\tau _1 \left( \beta _4 \psi _3 -\beta _2 \psi _3 ^3\right) -4 \beta _1 \psi _3 ^3+2 \beta _3 \psi _3 \right) \sin \tau _1\psi _3+5 \psi _3 ^4. \end{aligned}$$

(34)

From equation (33) if $\dfrac{d\lambda }{d\tau _2}>0$, then Hopf bifurcation occur at $\tau _2=\tau _{2,0}$.

Theorem 3.3

If $R_1$ and $S_2$ holds with $\tau _1 \in (0,\tau _1')$ then, there exists $\tau _2'$ such that endemic equilibrium point is asymptotically stable for $\tau _2 < \tau _2'$ and $\tau _2 > \tau _2'$, where $\tau _2'=\min \{\tau _{2,j}\}$ in (31). Furthermore, the model (1) undergoes Hopf bifurcation at $\tau _2=\tau _2'$.

Theorem 3.4

If endemic equilibrium point $E^*$ for $\tau _2 \in (0,\tau _2')$ then, there exists $\tau _1'$ such that endemic equilibrium point $E^*$ is asymptotically stable for $\tau _1 < \tau _1'$ and $\tau _1 > \tau _1'$, where $\tau _1'=\min \{\tau _{1,j}\}$ in (35). Furthermore, the model (1) undergoes Hopf bifurcation at $\tau _1=\tau _1'$.

$$\begin{aligned} \tau _{1,j}=\dfrac{1}{\psi _0}\arccos \{\frac{ \left( \delta _3 \rho _2+\delta _5 \delta _7\right) \cos \tau _2\psi _0-\delta _3 \rho _2+\delta _6 \delta _7+\left( -\delta _3 \rho _1-\delta _7 \rho _2\right) \sin \tau _2\psi _0}{\delta _7^2-\delta _3}\}+\dfrac{2\pi j}{\psi _0}. \end{aligned}$$

(35)

where

$$\begin{aligned} j&=0,1,2,\ldots ,\\ \delta _5&=\gamma _1 \psi _0 ^4-\gamma _2 \psi _0 ^3+\gamma _4 \psi _0,\\ \delta _7&=\psi _0 ^5-\alpha _2 \psi _0 ^3+\alpha _4 \psi _0 ,\\ \delta _7&=\beta _2 \psi _0 ^3+\beta _4 \psi _0. \end{aligned}$$

(36)

Parametric evaluation with hybrid genetic algorithm

A hybrid genetic algorithm combines the power of the genetic algorithm (GA) with the speed of a local optimizer.

The parametric approximation is the most challenging task after designing a mathematical model and after finding the intervals of stability, i.e. the parameters that satisfy the stability criteria. Optimizing parametric values for mathematical models has always remained a great challenge Abdel-Salam et al. (2021).

With the advancement in the field of artificial intelligence and data sciences, the parametric approximation is made easier, keeping in view the stochastic, probabilistic and/or the randomized nature of the real data sets.

In this manuscript, we have used a hybrid optimization tool, partially based on the genetic algorithm, that works for several populations of the parametric mutated genes (sets of values). Matlab platform was utilized for this purpose. Furthermore, the parametric values are selected by keeping in view the intervals imposed by the biological characteristics of the viral process of infection.

A continuous genetic algorithm, that can easily hybridize with the local optimizer, is used during this research. In simple words, the improved values from the genetic algorithm are carried forward by the local optimizer to reduce the computational complexity.

Numerical simulations

We have run some numerical experiments for the understanding of virus control and on the other hand, the bifurcation, linked with the delay.

Figure 3 depicts the role of important parameter b, in understanding the virus spread. For different values of b, we have obtained different dynamics and since the virus replication rate is directly proportional to b, for increased values of b, the virus spread increases and the phase space provides a better understanding of increase in infection, relative to virus load, target cells and the Furin action (see arrow indicating the peak in amplitude). Similarly, Fig. 4 provides information about the change in parameter, linked with the different infection stages (i.e. moving from the compartment of infected cells at first stage to infected cells at second stage). The change in angle of the phase portrait provides useful information about the dynamics.

Figure 5 provides useful information about the impact of delay in transmission from one compartment to another, on the virus replication, infected cells and Furin. We can see that for increased delay, as anticipated analytically, there is bifurcation.

Fig. 3

Impact of virus reproduction on: a virus load, b phase plot for healthy cells, virus load and Furin

Fig. 4

Impact of infection stages on: a virus load, b phase plot for healthy cells, virus load and Furin

Fig. 5

Impact of delay on: a virus load, b phase plot for healthy cells, virus load and Furin

Summary of results

A mathematical model is analyzed with non-negativity of solution, equilibrium points and stability analysis.

• 1. Theorem 2.1 shows that the values of compartments is always positive as the parameter is positive.

• 2. The Basic reproductive number is obtained. It is calculated by the model of ordinary differential equations, using analytical approach and Matcont numerical approach.

• 3. If basic reproductive number $R_0\le 1$, the infection free equilibrium point is stable and infection is completely vanished.

• 4. If the basic reproduction number $R_1 >1$, endemic equilibrium point is stable in feasible interval.

• 5. Here we use time delay as parameter of bifurcation to examine Hopf bifurcation.

• 6. The non negative endemic equilibrium point is stable when the time delay is very small as time delay increases, the instability occurs that is in accordance with the hopf bifurcation criteria.

  Hopf bifurcation is use to find out the instability region in the neighborhood of endemic equilibrium point.

• 7. Considering both the D614G mutation and the facilitated action of furin in this process, we assume parameters inclusive of these characteristics.

Discussion

The impact of the SARS-CoV2 virus is devastating mainly due to its speed of infection. The proposed model analyzes:

• 1. Action of enzyme “Furin” in the speed and spread of the virus.

• 2. Presence of D614G mutation (video S1).

• 3. Limiting value for $\eta$, i.e. the interaction rates.

• 4. Realistic connection of delay in time with the host and virus interactions.

• 5. Importance of delay in the interacting populations of infected cells at second stage, F(t) and the effect of interferon (IFN).

During this research, it is observed that the model is sensitive to the parameters. These parameters were taken from the literature as mentioned in the introduction and the mathematical modeling section. The parameters are responsible for the furin action and SARS-COV2 action. This fact is demonstrated well, with the aid of the numerical simulations, emerging from the Matcont software and genetic algorithm toolbox. The software has the facility for the parametric approximation as well as for the simulations with parametric sweep. The numerical experiments for different values of the parameters and the delay variable are presented in the previous section.

Conclusion

The impact of the CoViD-19 pandemic is devastating and scientific research seek to understand the mechanisms of infection, to create an appropriate vaccine. This paper analyzes the characteristics of the SARS-CoV2 viral infection that shows a fundamental adaptation in the infection process. Arg-Arg-Ala-Arg (RRAR) cleavage site “RRAR” is a cleavage site for the“convertase furin” pro-protein, and is found in the spike protein (S), exclusively in SARS-COV2 virus and is involved in the activation of S protein. In this manuscript, the action of Furin is demonstrated in detail with the aid of the IFN, virus and human cell interaction dynamics. Variable delay helped to link the model with the real dynamics. We conclude that the modeling approach can be further improved by linking it with the forthcoming results from the clinical trials.